Question 6:
Puan Rafidah wants to prepare a right circular cone shaped container in order to fill it with candies for her family Hari Raya Celebration. Diagram below shows the net of a right circular cone.


The circumference of the lid is 44 cm and its height is 24 cm.
Calculate the volume, in cm³ , of the container.
$\left[\pi =\frac{22}{7}\right]$

Solution:
$\begin{array}{l}2\pi r=44\\ 2\times \frac{22}{7}\times r=44\\ r=\frac{44}{2}\times \frac{7}{22}\\ r=7\text{ cm}\\ \text{Volume of cone}=\frac{1}{3}\pi r^{2}h\\ =\frac{1}{3}\times \frac{22}{7}\times 7^2\times 24\\ =1232{\text{ cm}}^3\end{array}$

Question 7:
A barrel contains 36 l of mineral water. ⅔ of the mineral water is mixed with 6 bottles of syrup, with a volume of 1.5 l each. The drink will be poured into a number of bottles with the same volume of 300 ml.
How many number of bottles needed?

Solution:
$\begin{array}{l}\text{Volume of mineral water}\\ =\frac{2}{3}\times 36l\\ =24l\\ \\ \text{Volume of syrup}\\ =6\times 1.5l=9l\\ \\ \text{Total volume}=24+9\\ =33l=33000ml\\ \\ \text{Number of bottles needed}\\ =\frac{33000}{300}=110\end{array}$

Question 8:
A spherical balloon expands such that its volume increases from 36π cm³ to 288π cm³ .
Find the increment of the radius, in cm, of the balloon.

Solution:
$\begin{array}{l}{V}_1=\frac{4}{3}\pi r_1{}^3\\ \frac{4}{3}\pi r_1{}^3=36\pi \\ r_1{}^3=36\pi \times \frac{3}{4\pi }\\ r_1{}^3=27\\ r_1=3\text{ cm}\\ \\ V_2=\frac{4}{3}\pi r_2{}^3\\ \frac{4}{3}\pi r_2{}^3=288\pi \\ r_2{}^3=288\pi \times \frac{3}{4\pi }\\ r_2{}^3=216\\ r_2=6\text{ cm}\\ \\ \text{Increment}=r_2-r_1\\ =6-3\\ =3\text{ cm}\end{array}$

Question 9:
A boy is given three pieces of cards by his teacher. The cards consist of one rectangle card and two circle cards of the same size as shown in the diagram below. The circumference of each circle is 66 cm.

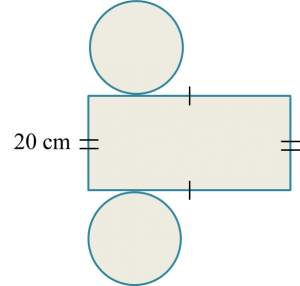
He is required to combine the cards to form a right circular cylinder.
Calculate the volume, in cm³, of the right circular cylinder.

Solution:
$\begin{array}{l}2\pi r=66\\ 2\times \frac{22}{7}\times r=66\\ r=\frac{66\times 7}{2\times 22}\\ =10.5\text{ cm}\\ \\ \text{Volume}=\pi r^{2}h\\ =\frac{22}{7}\times {10.5}^2\times 20\\ =6930{\text{ cm}}^3\end{array}$

Question 10:
Diagram below shows cube P and cube Q with the total surface area of 726 cm² and 1014 cm² respectively.

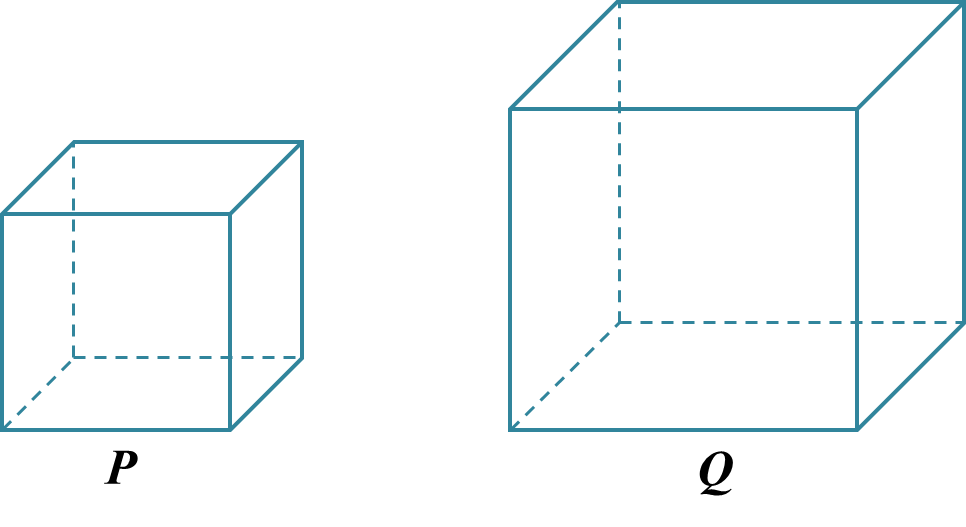Find the difference in volume between cube P and cube Q.

Solution:
$\begin{array}{l}\text{Area of one surface area of cube }P=\frac{726}{6}=121{\text{ cm}}^2\\ x\left(\text{Length}\right)\times x\left(\text{Width}\right)=121\\ x^2=121\\ x=11\\ \\ \text{Area of one surface area of cube }Q=\frac{1014}{6}=169{\text{ cm}}^2\\ y\left(\text{Length}\right)\times y\left(\text{Width}\right)=169\\ y^2=169\\ y=13\\ \\ \text{Difference in volume}\\ ={13}^3-{11}^3\\ =2197-1331\\ =866{\text{ cm}}^3\end{array}$

$\begin{array}{l}\text{Volume of a cone}\\ =\frac{1}{3}\pi r^{2}h\\ =\frac{1}{\cancel{3}}\times \frac{22}{\cancel{7}}\times 7^{\cancel{2}}\times \cancel{6}2\\ =308{\text{cm}}^3\end{array}$

 

In the pyramid shown, the base is a rectangle.

$\begin{array}{l}\text{Height of the}△=\sqrt{{10}^2-6^2}\\ =\sqrt{64}\\ =8cm\\ \\ \text{Volume of prism}\\ =\text{Area of cross section}\times \text{Length}\\ =\left(\frac{1}{\cancel{2}}\times {\cancel{12}}^6\times 8\right)\times 16\\ =768c{m}^3\end{array}$

$\begin{array}{l}V=\frac{1}{3}\pi r^{2}h\\ h=\frac{3V}{\pi r^2}\\ =\frac{3\times 77}{\frac{22}{7}\times 3.5\times 3.5}\\ =6\text{ cm}\end{array}$