Question 10 (4 marks):
Given the function g : x → 2x – 8, find
(a) g−1(x),(b) the value of p such that g2(3p2)=30.
Solution:
(a)
Let y=g(x)=2x−82x−8=y 2x=y+8 x=y+82Thus, g−1(x)=x+82
(b)
g(x)=2x−8g2(x)=g[g(x)] =g(2x−8) =2(2x−8)−8 =4x−16−8 =4x−24g2(3p2)=304(3p2)−24=306p=54p=9
Given the function g : x → 2x – 8, find
(a) g−1(x),(b) the value of p such that g2(3p2)=30.
Solution:
(a)
Let y=g(x)=2x−82x−8=y 2x=y+8 x=y+82Thus, g−1(x)=x+82
(b)
g(x)=2x−8g2(x)=g[g(x)] =g(2x−8) =2(2x−8)−8 =4x−16−8 =4x−24g2(3p2)=304(3p2)−24=306p=54p=9
Question 11 (4 marks):
Diagram 9 shows the relation between set A, set B and set C.
 Diagram 9
Diagram 9
It is given that set A maps to set B by the function x+12 and maps to set C by fg : x → x2 + 2x + 4.
(a) Write the function which maps set A to set B by using the function notation.
(b) Find the function which maps set B to set C.
Solution:
 (a)
(a)
g:x→x+12
(b)
g(x)=x+12fg(x)=x2+2x+4f[g(x)]=x2+2x+4f(x+12)=x2+2x+4Let x+12=yx+1=2yx=2y−1∴
Diagram 9 shows the relation between set A, set B and set C.
 Diagram 9
Diagram 9It is given that set A maps to set B by the function x+12 and maps to set C by fg : x → x2 + 2x + 4.
(a) Write the function which maps set A to set B by using the function notation.
(b) Find the function which maps set B to set C.
Solution:
 (a)
(a)g:x→x+12
(b)
g(x)=x+12fg(x)=x2+2x+4f[g(x)]=x2+2x+4f(x+12)=x2+2x+4Let x+12=yx+1=2yx=2y−1∴


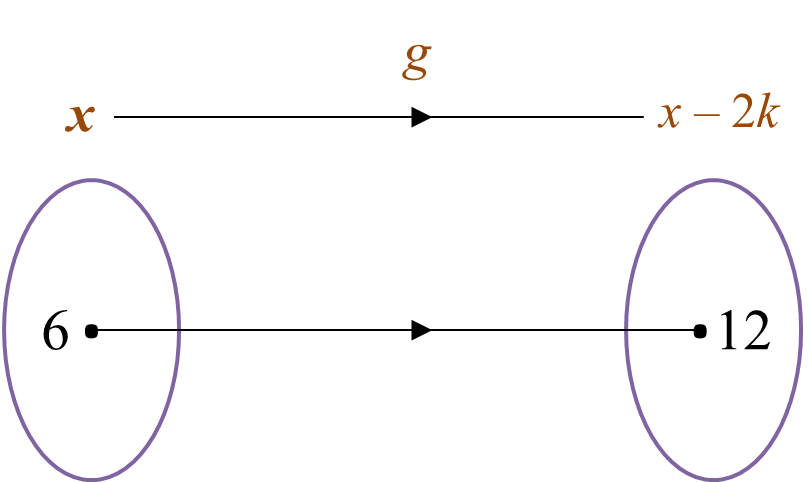
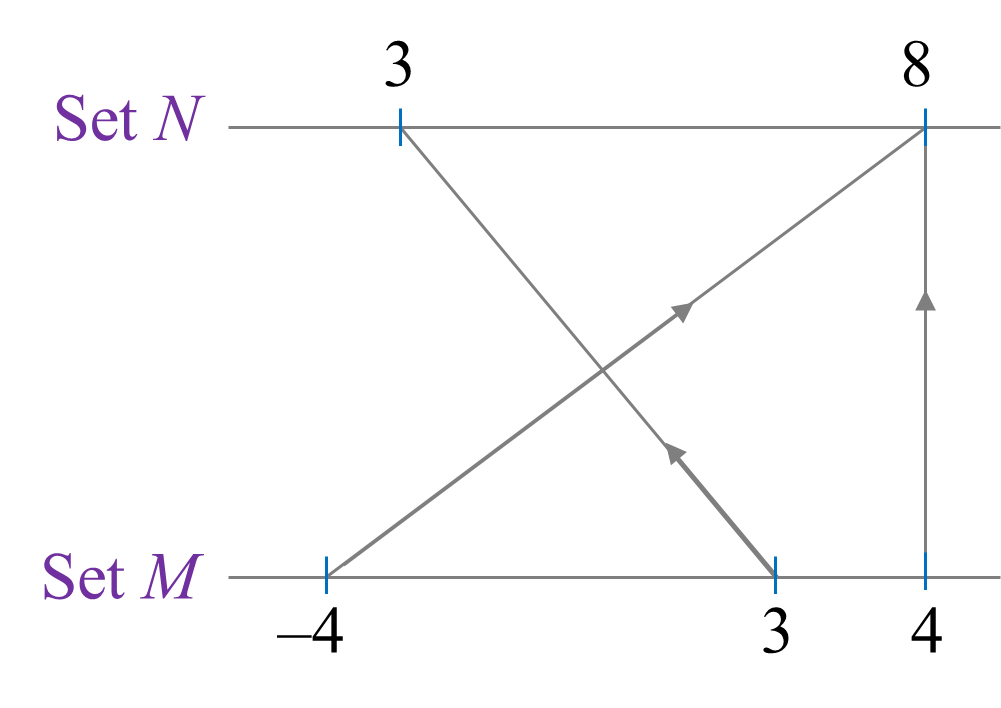
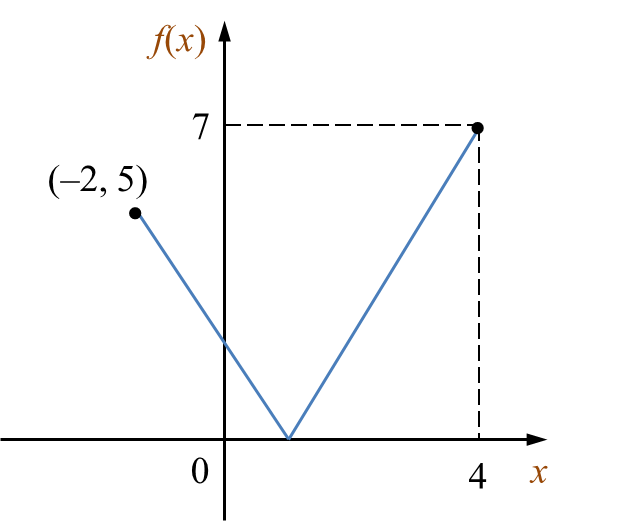 Diagram
Diagram 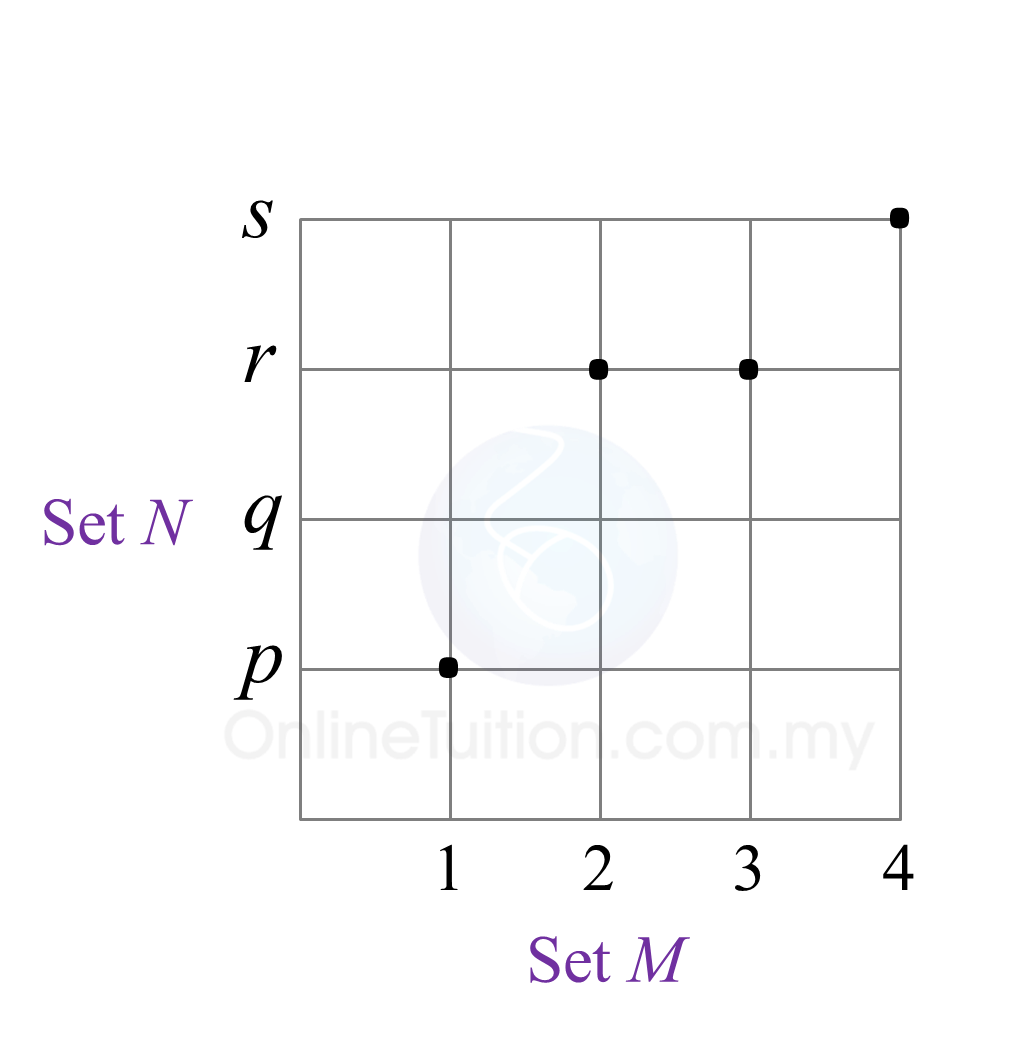 State
State