Short Questions (Question 1 & 2)

Posted on April 23, 2020 by user

Question 1:

Diagram below shows the graph of a binomial distribution of X.

(a) the value of h,

(b) P (X ≥ 3)

Solution:

(a)

P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4) = 1

\begin{array}{l} \frac{1}{16} + \frac{1}{4} + h + \frac{1}{4} + \frac{1}{16} = 1 \\ h = 1 - \frac{5}{8} \\ h = \frac{3}{8} \end{array}

(b)

P (X ≥ 3) = P (X = 3) + P (X = 4)

P (X \geq 3) = \frac{1}{4} + \frac{1}{16} = \frac{5}{16}

Question 2:

The random variable X represents a binomial distribution with 10 trails and the probability of success is ¼.

(a) the standard deviation of the distribution,

(b) the probability that at least one trial is success.

Solution:

(a)

n = 10, p = ¼

\begin{array}{l} Standard deviation = \sqrt{n p q} \\ = \sqrt{10 \times \frac{1}{4} \times \frac{3}{4}} \\ = 1.875 \end{array}

(b)

\begin{array}{l} P (X = r) = C_{r} {(\frac{1}{4})}^{r} {(\frac{3}{4})}^{10 - r} \\ P (X \geq 1) \\ = 1 - P (X < 1) \\ = 1 - P (X = 0) \\ = 1 - C_{0} {(\frac{1}{4})}^{0} {(\frac{3}{4})}^{10} \\ = 0.9437 \end{array}

8.1b Mean, Variance And Standard Deviation Of A Binomial Distribution

Posted on April 23, 2020 by user

8.1b Mean, Variance and Standard Deviation of a Binomial Distribution

2. Determine the mean, variance and standard deviation of binomial distribution.

If X is a binomial discrete random variable such that X ~ B (n, p),

then

Mean of X,

μ = n p

Variance of X,

σ^{2} = n p q

Standard deviation of X,

σ = \sqrt{n p q}

Example 1:

A Football club organises a practice session for trainees on scoring goals from penalty kicks. Each trainee takes 8 penalty kicks. The probability that a trainee scores a goal from a penalty kick is p. After the session, it is found that the mean number of goals for a trainee is 7.2.

Find the value of p.

Solution:

Mean = np

np = 7.2

8p = 7.2

p = 0.9

Example 2:

X is a binomial random variable such that X ~ B (n, p). If its mean and standard deviation are 90 and

3 \sqrt{7}

respectively, find the value of p and of n.

Solution:

\begin{array}{l} Mean = 90 \\ n p = 90 \\ Standard deviation = 3 \sqrt{7} \\ \sqrt{n p q} = 3 \sqrt{7} \\ n p q = 9 (7) \leftarrow Square both sides \\ n p q = 63 \\ (n p) q = 63 \\ 90 q = 63 \\ q = \frac{7}{10} \\ ∴ p = 1 - \frac{7}{10} = \frac{3}{10} \\ From n p = 90, \\ n (\frac{3}{10}) = 90 \\ n = 300 \end{array}

7.4 Probability of Independent Events

Posted on April 23, 2020 by user

7.4 Probability of Independent Events

1. In an experiment, if the outcomes of event A do not influence the outcomes of event B, then the two events are independent.

2. If A and B are two independent events, the probability for the occurrence of events A and B is

P (A ∩ B) = P (A) × P (B)

3. The concept of the probability of two independent events can be expanded to three or more independent events. If A, B and C are three independent events, the probability for the occurrence of events A, B and C is

P (A ∩ B ∩ C) = P (A) x P (B) x P (C)

4. A tree diagram can be constructed to show all the possible outcomes of an experiment.

Example:

Fatimah, Emily and Rani are to take a written driving test. The probability that they pass the test are ½, ⅔ and ¾ respectively. Calculate the probability that

(a) only one of them passes the exam,

(b) at least two of them pass the exam,

Solution:

Let P = Pass and F = Fail

The tree diagram is as follows.

(a)

P (only one of them passes the exam)

= P(PFF or FPF or FFP)

= P(PFF) + P(FPF) + P(FFP)

\begin{array}{l} = \frac{1}{24} + \frac{1}{12} + \frac{1}{8} \\ = \frac{1}{4} \end{array}

(b)

P (at least two of them pass the exam)

= P (PPP or PPF or PFP or FPP)

= P (PPP) + P (PPF) + P (PFP) + P (FPP)

\begin{array}{l} = \frac{1}{4} + \frac{1}{12} + \frac{1}{8} + \frac{1}{4} \\ = \frac{17}{24} \end{array}

(c)

P (at least one of them passes the exam)

= 1 – P (all of them fail)

= 1 – P (FFF)

\begin{array}{l} = 1 - \frac{1}{24} \\ = \frac{23}{24} \end{array}

Long Questions (Question 1)

Posted on April 23, 2020 by user

Question 1:

Peter, William and Roger compete with each other in shooting a target. The probabilities that they strike the target are

\frac{2}{5}, \frac{3}{4} and \frac{2}{3}

respectively. Calculate the probability that

(a) all the three of them strike the target,

(b) only one of them strikes the target,

Solution:

Let S = Strike and M = Missed

\begin{array}{l} Probability of Peter missed the target = \frac{3}{5} \\ Probability of William missed the target = \frac{1}{4} \\ Probability of Roger missed the target = \frac{1}{3} \end{array}

(a)

\begin{array}{l} Probability (all three persons strike the target) \\ = \frac{2}{5} \times \frac{3}{4} \times \frac{2}{3} \\ = \frac{1}{5} \end{array}

(b)

\begin{array}{l} Probability (only one of them strikes the target) \\ = P (only Peter struck) + P (only William struck) + P (only Roger struck) \\ = (\frac{2}{5} \times \frac{1}{4} \times \frac{1}{3}) + (\frac{3}{5} \times \frac{3}{4} \times \frac{1}{3}) + (\frac{3}{5} \times \frac{1}{4} \times \frac{2}{3}) \\ = \frac{1}{30} + \frac{3}{20} + \frac{1}{10} \\ = \frac{17}{60} \end{array}

(c)

\begin{array}{l} Probability (at least one of them strikes the target) \\ = 1 - P (all missed the target) \\ = 1 - (\frac{3}{5} \times \frac{1}{4} \times \frac{1}{3}) \\ = 1 - \frac{1}{20} \\ = \frac{19}{20} \end{array}

7.2 Probability of the Combination of Two Events

Posted on April 23, 2020 by user

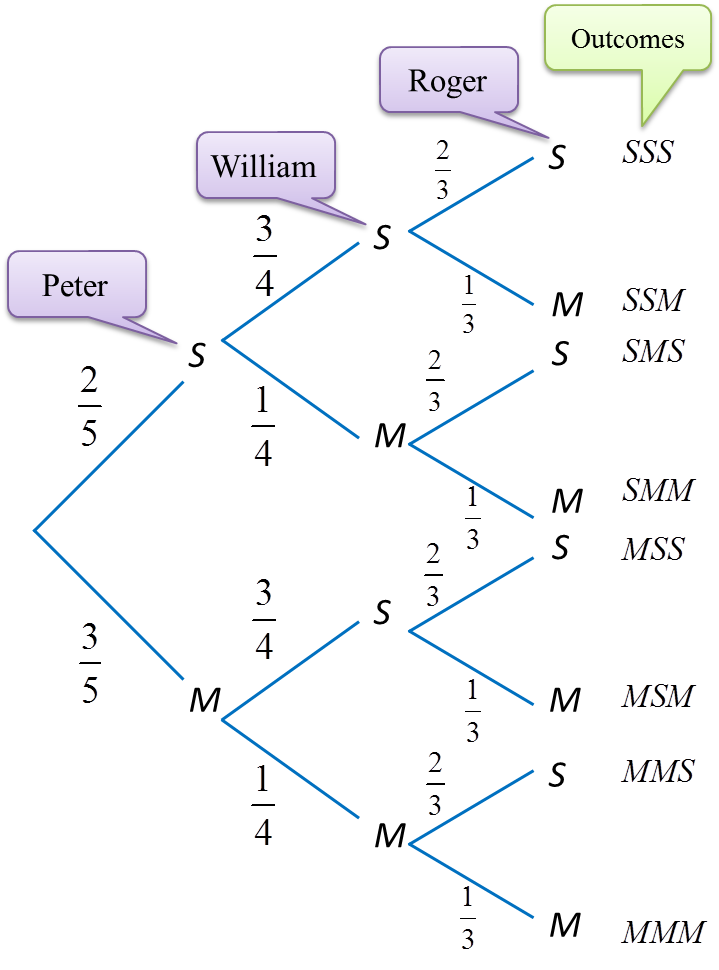
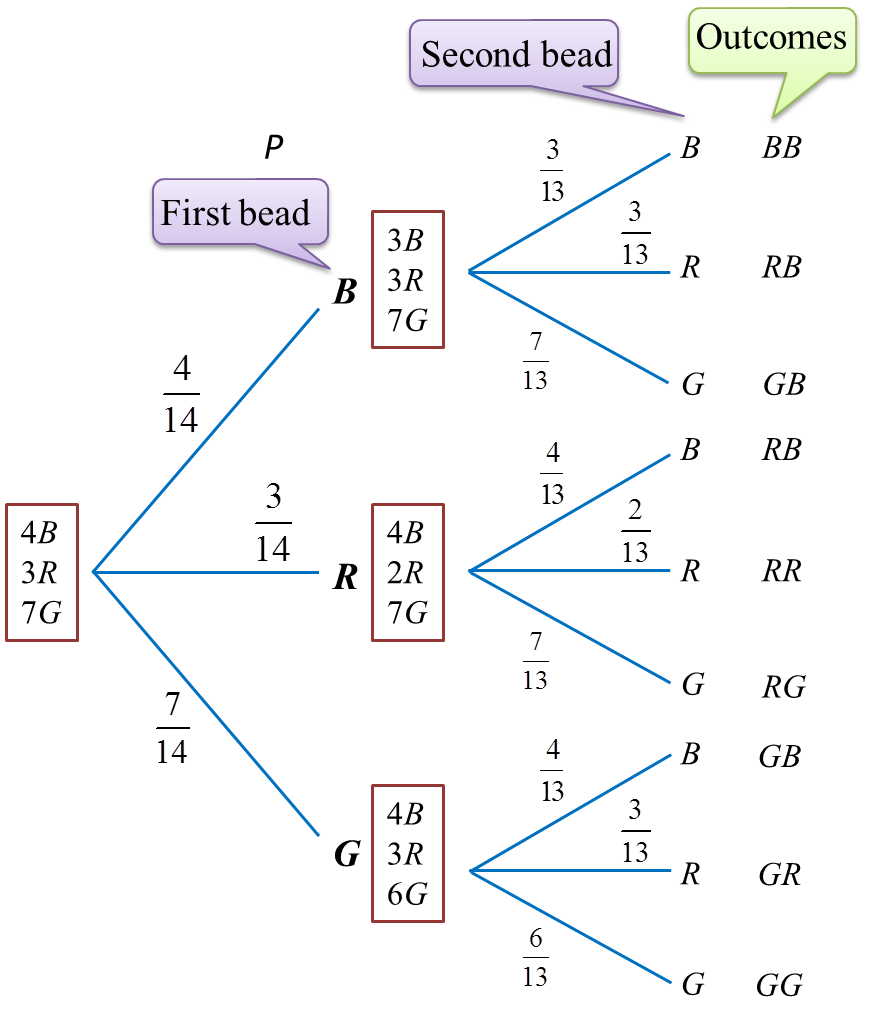
7.2 Probability of the Combination of Two Events

1. For two events, A and B, in a sample space S, the events A ∩ B (A and B) and A υ B (A or B) are known as combined events.

2. The probability of the union of sets A and B is given by:

P (A \cup B) = P (A) + P (B) - P (A \cap B)

3. The probability of the union of sets A and B can also be calculated using an alternative method, i.e.

P (A \cup B) = \frac{n (A \cup B)}{n (S)}

4. The probability of event A and event B occurring, P(A ∩ B) can be determined by the following formula.

P (A \cap B) = \frac{n (A \cap B)}{n (S)}

Example:

Given a universal set ξ = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. A number is chosen at random from the set ξ . Find the probability that

(a) an even number is chosen.

(b) an odd number or a prime number is chosen.

Solution:

The sample space, S = ξ

n(S) = 14

(a)

Let A = Event of an even number is chosen

A = {2, 4, 6, 8, 10, 12, 14}

n (A) = 7

\begin{array}{l} P (A) = \frac{n (A)}{n (S)} \\ = \frac{7}{14} = \frac{1}{2} \end{array}

(b)
Let,

B = Event of an odd number is chosen

C = Event of a prime number is chosen

B = {3, 5, 7, 9, 11, 13, 15} and n (B) = 7

C = {2, 3, 5, 7, 11, 13} and n (C) = 6

The event when an odd number or a prime number is chosen is B υ C.

P (B υ C) = P (B) + P (C) – P (B ∩ C)

B ∩ C = {3, 5, 7, 11, 13}, n (B ∩ C) = 5

\begin{array}{l} P (B \cup C) \\ = P (B) + P (C) - P (B \cap C) \\ = \frac{n (B)}{n (S)} + \frac{n (C)}{n (S)} - \frac{n (B \cap C)}{n (S)} \\ = \frac{7}{14} + \frac{6}{14} - \frac{5}{14} \\ = \frac{8}{14} = \frac{4}{7} \\ ∴ The probability of choosing an \\ odd number or a prime number = \frac{4}{7} . \end{array}

Short Questions (Question 1 to 3)

Posted on April 23, 2020 by user

Question 1:

The probability of student P being chosen as a school prefect is

\frac{3}{4}

while the probability of student Q being chosen is

\frac{5}{6}

Find the probability that

(a) both of the students are chosen as the school prefect,

(b) only one student is chosen as a school prefect.

Solution:

(a)

\begin{array}{l} Probability (both of the students are chosen as the school prefect) \\ = \frac{3}{4} \times \frac{5}{6} \\ = \frac{5}{8} \end{array}

(b)

\begin{array}{l} Probability (only one student is chosen as a school prefect) \\ = (\frac{3}{4} \times \frac{1}{6}) + (\frac{1}{4} \times \frac{5}{6}) \\ = \frac{3}{24} + \frac{5}{24} \\ = \frac{1}{3} \end{array}

Question 2:

A bag contains x pink cards and 6 green cards. Two cards are drawn at random from the bag, one after the other, without replacement. Find the value of x if the probability of obtaining two green cards is ⅓.

Solution:

Total cards in the bag = x + 6

P(obtaining 2 green cards) = ⅓

\begin{array}{l} \frac{6}{x + 6} \times \frac{5}{x + 5} = \frac{1}{3} \\ \frac{30}{(x + 6) (x + 5)} = \frac{1}{3} \end{array}

(x + 6) (x + 5) = 90

x² + 11x + 30 = 90

x² + 11x – 60 = 0

(x – 4) (x + 15) = 0

x = 4 or x = –15 (not accepted)

Question 3:
A sample space of an experiment is given by S = {1, 2, 3, … , 21}. Events Q and R are defined as follows:
Q : {3, 6, 9, 12, 15, 18, 21}
R : {1, 3, 5, 15, 21}

Find
(a) P(Q)
(b) P(Q and R)

Solution:
(a)

\begin{array}{l} n (S) = 21, n (Q) = 7 \\ P (Q) = \frac{7}{21} = \frac{1}{3} \end{array}

(b)

\begin{array}{l} Q \cap R = {3, 15, 21}, \\ t h e n n (Q \cap R) = 3 \\ P (Q and R) = P (Q \cap R) \\ = \frac{n (Q \cap R)}{n (S)} \\ = \frac{3}{21} \\ = \frac{1}{7} \end{array}

Long Questions (Question 2 & 3)

Posted on April 23, 2020 by user

Question 2:

A bag contains 4 red cards, 6 blue cards and 5 green cards. A card is drawn at random and its colour is recorded and then it is returned to the bag before the second card is drawn at random. Find the probability that

(a) all the three cards are blue,

(b) there are two blue cards followed by one red card,

(d) all the three cards have the same colour.

Solution:

Let R = red card, B = blue card, G = green card

(a)

\begin{array}{l} Probability (all the three cards are blue) \\ = \frac{6}{15} \times \frac{6}{15} \times \frac{6}{15} \\ = \frac{8}{125} \end{array}

(b)

\begin{array}{l} Probability (two blue cards followed by one red card) \\ = \frac{6}{15} \times \frac{6}{15} \times \frac{4}{15} \\ = \frac{16}{375} \end{array}

(c)

\begin{array}{l} Probability (the sequence of the cards drawn is red, green and blue) \\ = \frac{4}{15} \times \frac{6}{15} \times \frac{5}{15} \\ = \frac{8}{225} \end{array}

(d)

\begin{array}{l} Probability (all the three cards have the same colour) \\ = P (R R R) + P (B B B) + P (G G G) \\ = {(\frac{4}{15})}^{3} + {(\frac{6}{15})}^{3} + {(\frac{5}{15})}^{3} \\ = \frac{64}{3375} + \frac{216}{3375} + \frac{125}{3375} \\ = \frac{3}{25} \end{array}

Question 3:

A bag contains 4 blue beads, 3 red beads and 7 green beads. Two beads are drawn at random from the bag, one after the other without replacement. Find the probability that

(a) both the beads are of the same colour,

(b) both the beads are of different colours.

Solution:

(a)

\begin{array}{l} Probability (both the beads are of the same colour) \\ = P (blue, blue) + P (red, red) + P (green, green) \\ = (\frac{4}{14} \times \frac{3}{13}) + (\frac{3}{14} \times \frac{2}{13}) + (\frac{7}{14} \times \frac{6}{13}) \\ = \frac{6}{91} + \frac{3}{91} + \frac{3}{13} \\ = \frac{30}{91} \end{array}

(b)

\begin{array}{l} Probability (both the beads are of different colour) \\ = 1 - P (both the beads are of the same colour) \\ = 1 - \frac{30}{91} \leftarrow From part (a) \\ = \frac{61}{91} \end{array}

7.1 Probability of an Event

Posted on April 23, 2020 by user

7.1 Probability of an Event

1. An experiment is a process or an action in making an observation to obtain the require results.

2. An outcome of an experiment is a possible result that can be obtained from the experiment.

3. A sample space of an experiment is the set of all the possible outcomes of an experiment.

4. The probability for the occurrence of an event A in the sample space S is

P (A) = \frac{number of outcomes of event A}{number of outcomes of sample space S}

P (A) = \frac{n (A)}{n (S)}

5. (a) The range of values of a probability is .

(b) If P (A) = 1, event A is sure to occur.

(c) If P (A) = 0, event A will not occur.

6. The complement of an event A is denoted by ̅A and the probability of a complementary event is given by

P (\bar{A}) = 1 - P (A)

Example:

A box contains 20 cards. The cards are 21 to 40 respectively. If a card is chosen at random, find the probability of obtaining

(a) an even number,

(b) an odd number greater than 29.

Solution:

The sample space, S, is

S = {21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40}

n (S) = 20

(a)

A = Event of obtaining an even number

A = {22, 24, 26, 28, 30, 32, 34, 36, 38, 40}

n (A) = 10

\begin{array}{l} P (A) = \frac{n (A)}{n (S)} \\ = \frac{10}{20} = \frac{1}{2} \end{array}

(b)

B = Event of obtaining an odd number greater than 29

B = {31, 33, 35, 37, 39}

n (B) = 5

\begin{array}{l} P (B) = \frac{n (B)}{n (S)} \\ = \frac{5}{20} = \frac{1}{4} \end{array}

7.3 Probability of Mutually Exclusive Events

Posted on April 23, 2020 by user

7.3 Probability of Mutually Exclusive Events

1. Two events are mutually exclusive if they cannot occur at the same time.

2. If A and B are mutually exclusive events, then

P (A υ B) = P (A) + P (B)

Example:

A bag contains 3 blue cards, 4 green cards and 5 yellow cards. A card is chosen at random from the box. Find the probability that the chosen card is green or yellow.

Solution:

Let G = event when a green card is chosen.

Y = event when a yellow card is chosen.

The sample space, S = 12, n (S) = 12

n (G) = 4 and n (Y) = 5

\begin{array}{l} P (G) = \frac{n (G)}{n (S)} = \frac{4}{12} \\ P (Y) = \frac{n (Y)}{n (S)} = \frac{5}{12} \end{array}

Events G and Y cannot occur simultaneously because we cannot obtain green card and yellow card at the same time. Therefore, events G and Y are mutually exclusive.

\begin{array}{l} G \cap Y = \emptyset \\ P (G \cup Y) = P (G) + P (Y) \\ = \frac{4}{12} + \frac{5}{12} \\ = \frac{9}{12} = \frac{3}{4} \end{array}

6.1 Permutation Part 1

Posted on April 23, 2020 by user

(A) rs Multiplication Principle/ Rule

1. If an operation can be carried out in r ways and another operation can be carried out in s ways, then the number of ways to carry out both the operations consecutively is r × s, i.e. rs.

2. The rs multiplication principle can be expanded to three or more operations. If the numbers of ways for the occurrence of events A, B and C are r, s and p respectively, the number of ways for the occurrence of all the three events consecutively is r × s × p, i.e. rsp.

Example 1:
There are 3 different roads to travel from town P to town Q and 4 different roads to travel from town Q to town R. Calculate the number of ways a person can travel from town P to town R via town Q.

Solution:

3 × 4 = 12

(B) Permutations

Example 2:
Calculate each of the following.
(a) 7!
(b) 4!6!
(c) 0!5!

\begin{array}{l} (d) \frac{7!}{5!} \\ (e) \frac{8!}{4!} \\ (f) \frac{n!}{(n - 2)!} \\ (g) \frac{n! 0!}{(n - 1)!} \\ (h) \frac{3! (n + 1)!}{2! n!} \end{array}

Solution:

(a) 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

(b) 4!6! = (4 × 3 × 2 × 1)( 6 × 5 × 4 × 3 × 2 × 1) = 17280

(c) 0!5! = (1)( 5 × 4 × 3 × 2 × 1) = 120

\begin{array}{l} (d) \frac{7!}{5!} = \frac{7 \times 6 \times 5!}{5!} = 7 \times 6 = 42 \\ (e) \frac{8!}{4!} = \frac{8 \times 7 \times 6 \times 5 \times 4!}{4!} = 8 \times 7 \times 6 \times 5 = 1680 \\ (f) \frac{n!}{(n - 2)!} = \frac{n (n - 1) (n - 2)}{(n - 2)} = n (n - 1) \\ (g) \frac{n! 0!}{(n - 1)!} = \frac{n (n - 1) (1)}{(n - 1)} = n \\ (h) \frac{3! (n + 1)!}{2! n!} = \frac{3 \times 2! (n + 1) (n) (n - 1)}{2! n (n - 1)} = 3 (n + 1) \end{array}

Calculator Computation: