Question 3 (4 marks):
Diagram shows a standard normal distribution graph.
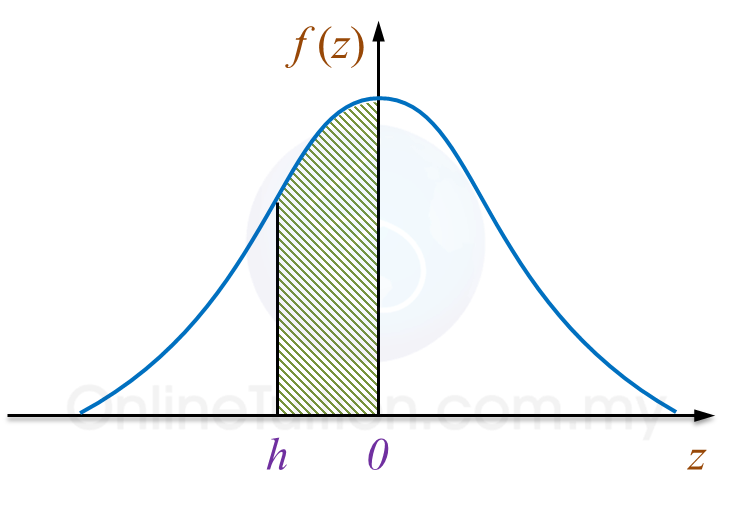 Diagram
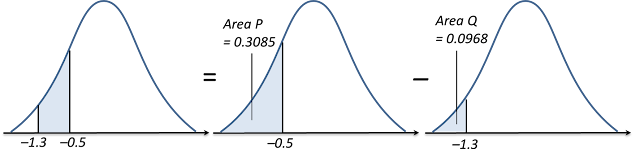
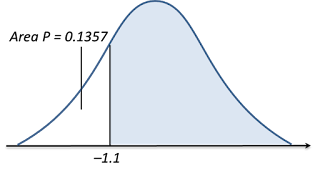
Diagram The probability represented by the area of the shaded region is 0.2881.
(a) Find the value of
h.
(b) X is a continuous random variable which is normally distributed with a mean, μ and a variance of 16.
Find the value of μ if the
z-score of
X = 58.8 is
h.
Solution:
(a)
P(
X <
h) = 0.5 – 0.2881
P(
X <
h) = 0.2119
P(
X < –0.8) = 0.2119
h = –0.8
(b)
Question 4 (4 marks):
A voluntary body organizes a first aid course 4 times per month, every Saturday from March until September.
[Assume there are four Saturdays in every month]
Salmah intends to join the course but she might need to spare a Saturday per month to accompany her mother to the hospital. The probability that Salmah will attend the course each Saturday is 0.8. Salmah will be given a certificate of monthly attendance if she can attend the course at least 3 times a month.
(a) Find the probability that Salmah will be given the certificate of monthly attendance.
(b) Salmah will qualify to sit for the first aid test if she obtains more than 5 certificates of monthly attendance.
Find the probability that Salmah qualifies to take the first aid test.
Solution:
(a)
(b)





 Diagram
Diagram 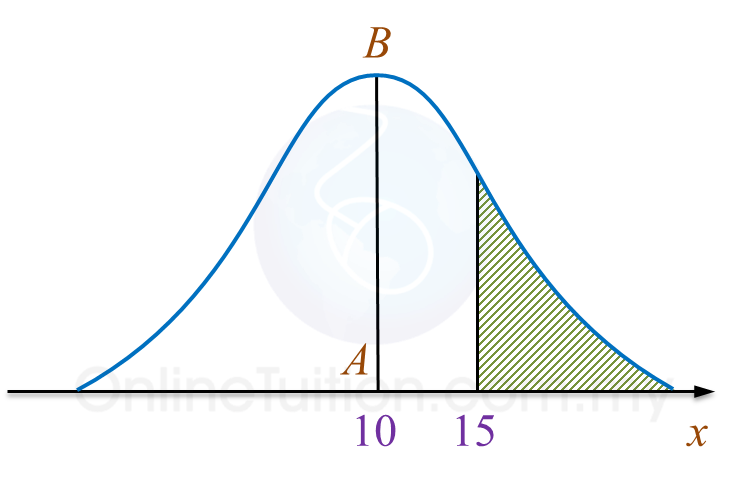 Diagram
Diagram 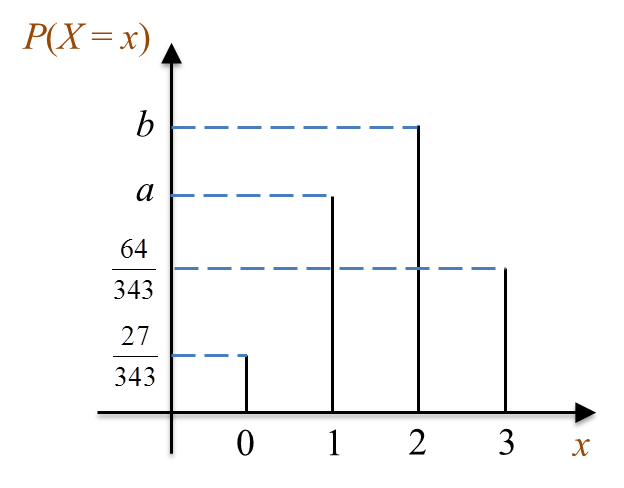 Diagram
Diagram 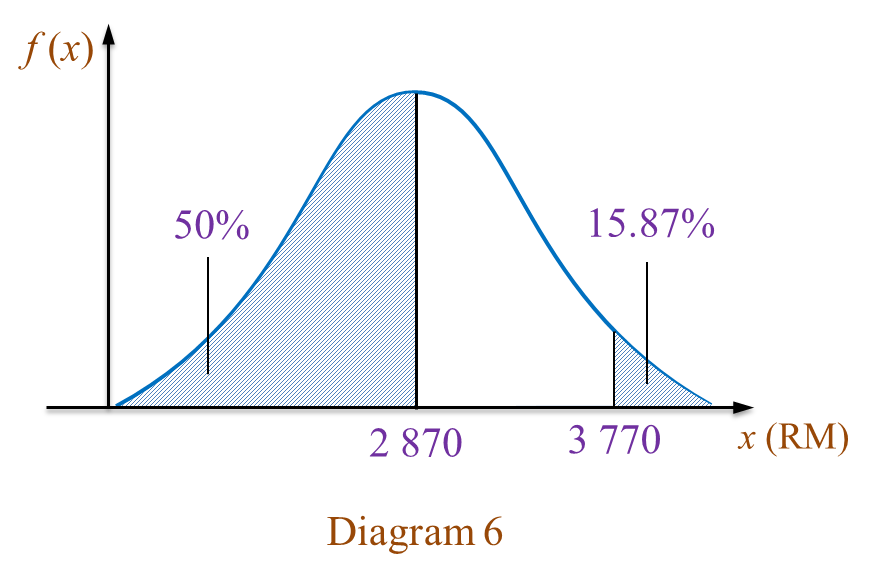 (a)(i) Find the standard deviation.
(a)(i) Find the standard deviation.