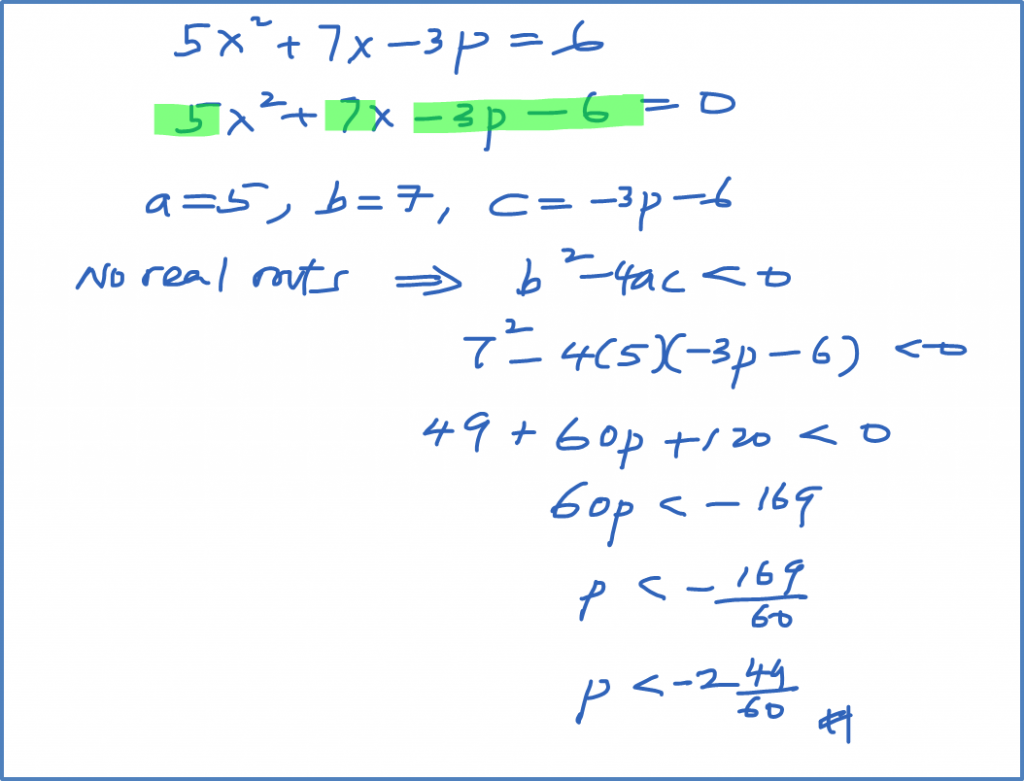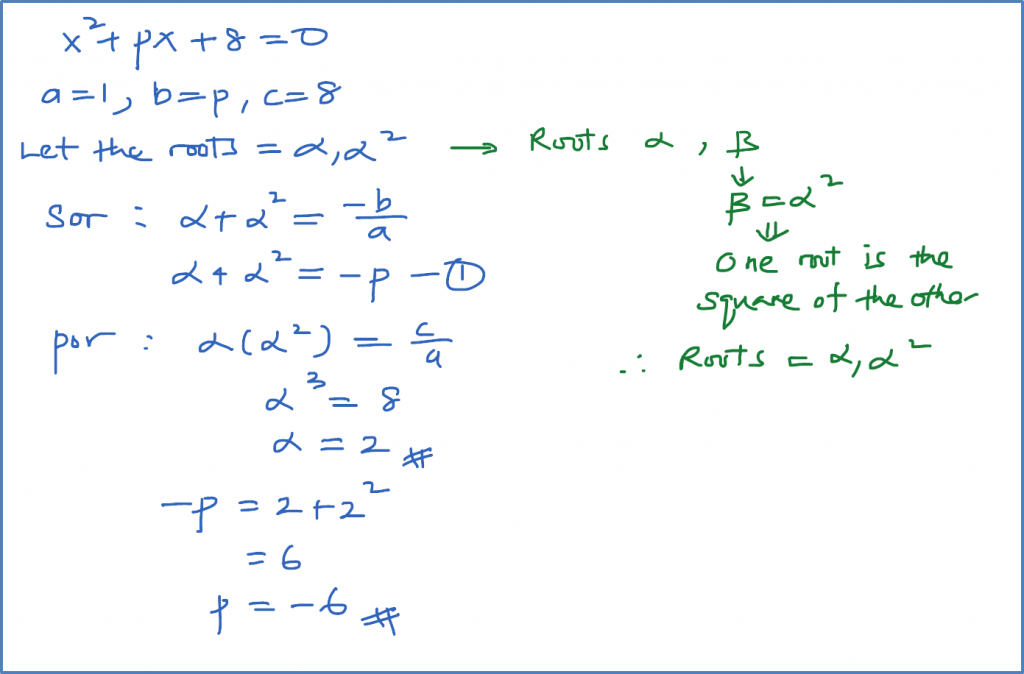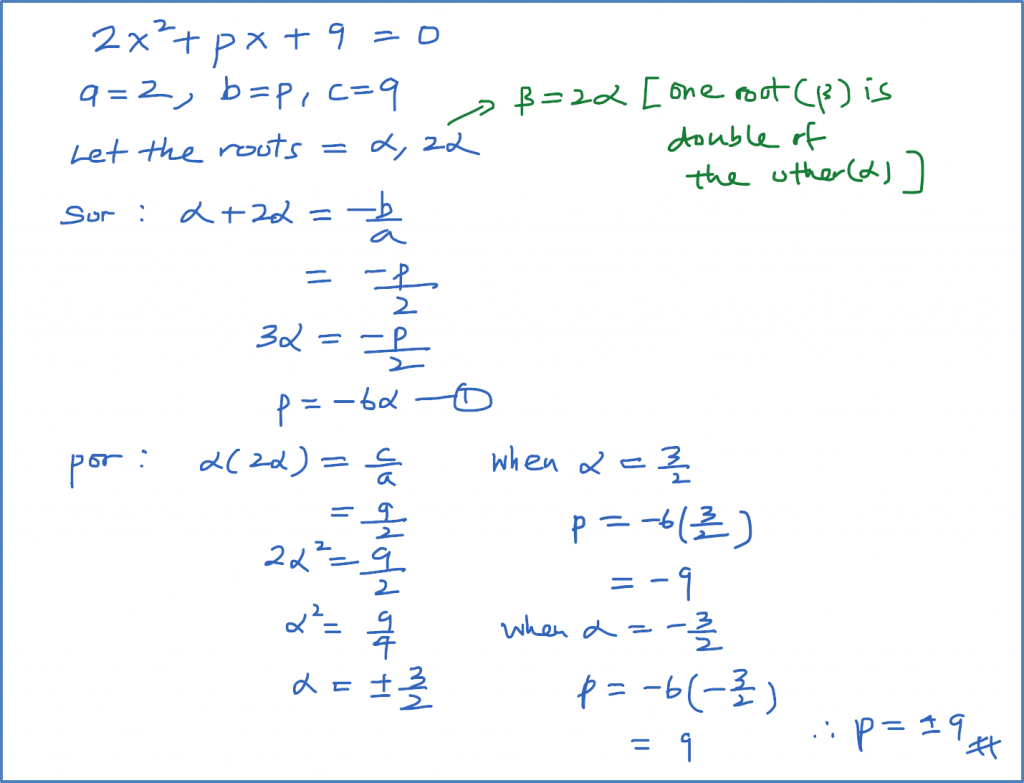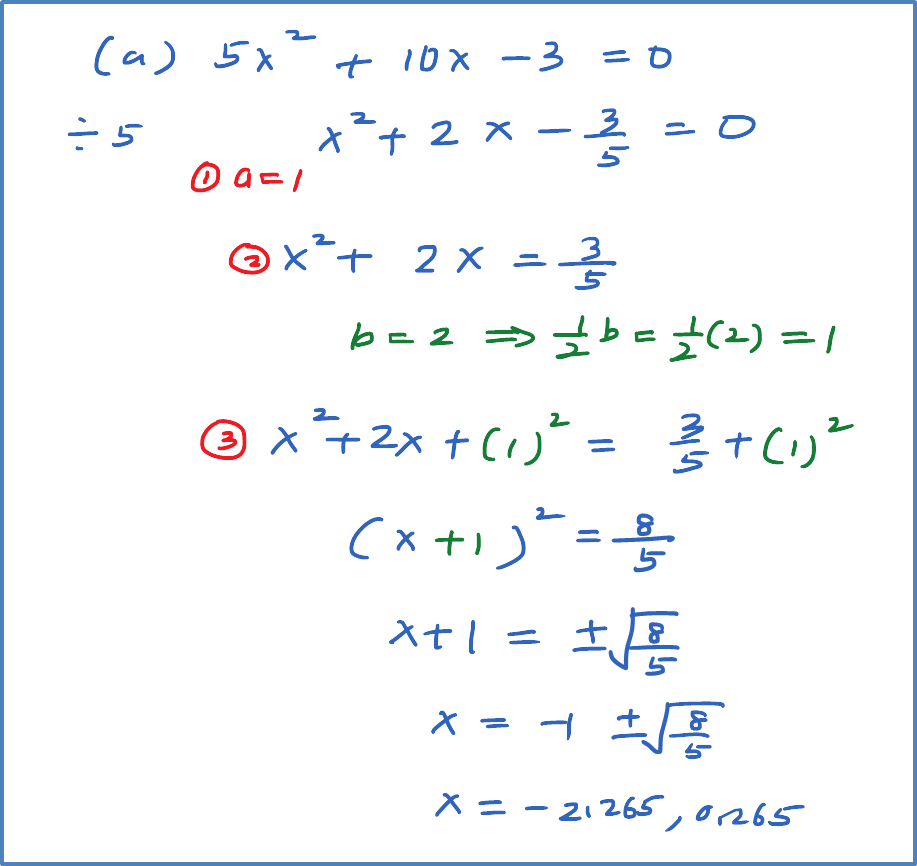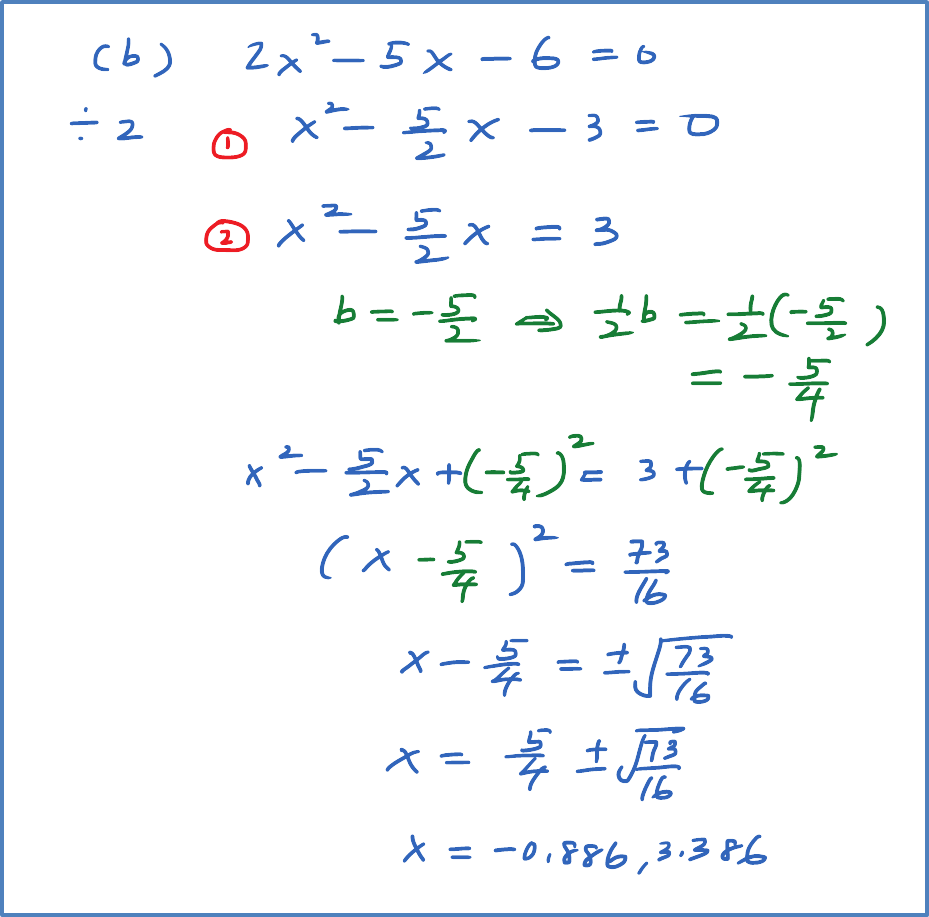3.3a Finding the Maximum and Minimum Points of Quadratic Function using Completing the Square (Examples)

Posted on April 18, 2020 by user

Example 1
Find the maximum or minimum value of each of the following quadratic function by completing the squares. In each case, state the value of x at which the function is maximum or minimum. And also, state the maximum or minimum point and axis of symmetry for each case.

(a)

$f (x) = x^{2} + 6 x + 7$
(b)

$f (x) = 2 x^{2} - 6 x + 7$
(c)

$f (x) = 5 - 2 x - x^{2}$
(d)

$f (x) = 4 + 12 x - 3 x^{2}$

3.3 Finding the Maximum and Minimum Points of Quadratic Function using Completing the Square

Posted on April 18, 2020 by user

Steps to convert general form of Quadratic Function into completing the square form

General form of quadratic function :

$f (x) = a x^{2} + b x + c$

Completing the square form :

$f (x) = a {(x + p)}^{2} + q$

Step 1 : Make sure the coefficient

$x^{2}$ is 1, if not factorize.
Step 2 : Insert

$+ {(\frac{c o e f f i c i e n t - o f x}{2})}^{2} - {(\frac{c o e f f i c i e n t - o f x}{2})}^{2}$
Step 3 : Completing the square [convert

$f (x) = a x^{2} + b x + c$ into

$f (x) = a {(x + p)}^{2} + q$ .]

3.2a Finding the Maximum/minimum and Axis of Symmetry of a Quadratic Function

Posted on April 18, 2020 by user

Example 1
State the maximum or minimum value of for each of the following quadratic function and state the value of x at which the function is maximum or minimum. Find the maximum or minimum point and finally state axis of symmetry for each case.

(a)

$f (x) = - 2 {(x - 3)}^{2} + 4$
(b)

$f (x) = 3 {(x - 4)}^{2} + 10$
(c)

$f (x) = - 3 {(x + 2)}^{2} - 9$
(d)

$f (x) = - 8 + 2 {(x + 5)}^{2}$

Correction for part (d) of the question,
when x + 5 = 0, x = -5
minimum point is (-5, -8)
Axis of symmetry, x = -5

3.1 Graph of Quadratic Functions

Posted on April 18, 2020 by user

The graph of quadratic function is parabola.
When the coefficient of x² is positive the graph is a parabola with ∪ shape.
When the coefficient of x² is negative the graph is a parabola with ∩ shape.

(A) Axis of Symmetry

The axis of symmetry is a vertical line passing through the maximum or minimum point of the parabola.

(A) General Form of Quadratic Function

Posted on April 18, 2020 by user

3.1 General Form of Quadratic Function

General form of a quadratic function is

$f (x) = a x^{2} + b x + c$ where a, b, and c are constants and a ≠ 0, and x as a variable.

Example:
Determine which of the following is a quadratic function.

$f (x) = (5 x - 3) (3 x + 8)$
$f (x) = 2 (3 x + 8)$
$f (x) = \frac{5}{2 x^{2}}$

Answer:
(a)

$\begin{array}{l} f (x) = (5 x - 3) (3 x + 8) \\ f (x) = 15 x^{2} + 40 x - 9 x - 24 \\ f (x) = 15 x^{2} + 31 x - 24 \end{array}$
Quadratic function

(b)

$\begin{array}{l} f (x) = 2 (3 x + 8) \\ f (x) = 6 x + 16 \end{array}$
Not quadratic function

(c) Not quadratic function

SPM Practice (Paper 1)

Posted on April 18, 2020 by user

Question 11:
The quadratic equation

$x^{2} - 4 x - 1 = 2 p (x - 5)$ , where p is a constant, has two equal roots. Calculate the possible values of p.

Solution:

Question 12:
Find the range of values of k for which the equation

$x^{2} - 2 k x + k^{2} + 5 k - 6 = 0$ has no real roots.

Solution:

Question 13:
Find the range of values of p for which the equation

$5 x^{2} + 7 x - 3 p = 6$ has no real roots.

Solution:

SPM Practice (Paper 1)

Posted on April 18, 2020 by user

Question 6:
Write and simplify the equation whose roots are the reciprocals of the roots of

$3 x^{2} + 2 x - 1 = 0$ , without solving the given equation.

Solution:

Question 7:
Find the value of p if one root of

$x^{2} + p x + 8 = 0$ is the square of the other.

Solution:

Question 8:
If one root of

$2 x^{2} + p x + 9 = 0$ is twice the other, find the values of p.

Solution:

SPM Practice (Paper 1)

Posted on April 18, 2020 by user

Question 1:
Solve the following quadratic equations by factorisation.

$\begin{array}{l} (a) x^{2} - 5 x - 10 = - 4 \\ (b) 3 - x - 2 x^{2} = 0 \\ (c) 11 a = 2 a^{2} + 12 \\ (d) \frac{2 x + 7}{3 x - 2} = x \end{array}$

Solution:

Question 2:
Solve the following quadratic equations by completing the square.

$\begin{array}{l} (a) 5 x^{2} + 10 x - 3 = 0 \\ (b) 2 x^{2} - 5 x - 6 = 0 \end{array}$

Solution:

2.4 Discriminant of a Quadratic Equation

Posted on April 18, 2020 by user

The Discriminant

The expression

$b^{2} - 4 a c$ in the general formula is called the discriminant of the equation, as it determines the type of roots that the equation has.

Example
Determine the nature of the roots of the following equations.
a.

$5 x^{2} - 7 x + 3 = 0$
b.

$x^{2} - 4 x + 4 = 0$
c.

$- 2 x^{2} + 5 x - 9 = 0$

Answer:

Posted in Quadratic Equations, SPM Add Maths

2.3d Forming New Quadratic Equation given a Quadratic Equation (Example)

Posted on April 18, 2020 by user

Example

If the roots of $x^{2} - 3 x - 7 = 0$ are α and β , find the equation whose roots are $α^{2} β$ and $α β^{2}$ .

Solution

Part 1 : Find SoR and PoR for the quadratic equation in the question

Part 2 : Form a new quadratic equation by finding SoR and PoR

Posted in Quadratic Equations, SPM Add Maths

Posts navigation

← Older posts

Newer posts →