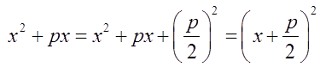2.4.2a Solving Quadratic Equations – Completing the Square (Examples)
(A) Steps to solve quadratic equation using completing the square
• make sure that the coefficient of x is 1.
• Rewrite the equation ax2 + bx + c = 0 in the form ax2 + bx = –c.
• Add (coefficient of x2)2(coefficient of x2)2 to both side of the equation.
• make sure that the coefficient of x is 1.
• Rewrite the equation ax2 + bx + c = 0 in the form ax2 + bx = –c.
• Add (coefficient of x2)2(coefficient of x2)2 to both side of the equation.
Example:
Solve the following quadratic equations by completing the square.
(a) x2 – 6x – 3 = 0
(a) x2 – 6x – 3 = 0
(b) 2x2 – 5x – 7 = 0
(c) x2 + 1 = 10x/3
Solution: