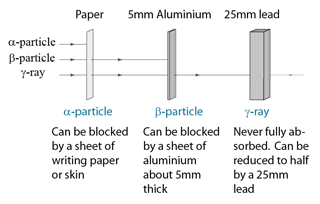
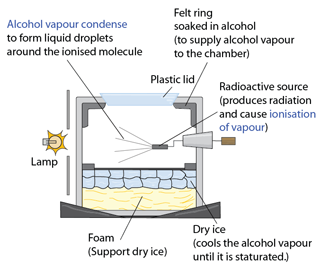
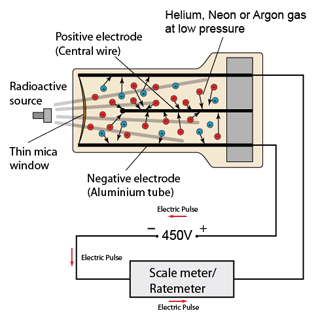
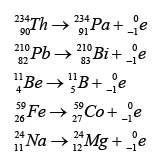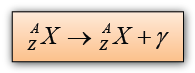Half-life

1. The half-life (T_½ ) of a quantity subject to exponential decay is the time required for the quantity (mass, number of atom or activity) to decay to half of its initial value.
2.  The decay curve of a radioactive source can be found experimentally - provided the activity of the source decreases over a practicable time period (minutes, hours or days for example). 
3. The corrected count-rate is then plotted against time to give the decay curve. The half-life of the source can be found from the curve as indicated above.

(Decay Curve)

Example 1
A radioisotope has half-life of 8 hours. Initially, there were 3.6 x 10¹⁸ radioisotope atoms in a sample. How much time is taken for the number of atoms of the radioisotope to fall to 4.5 x 10¹⁷?

Answer:

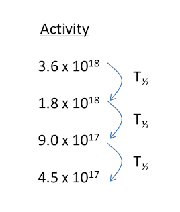The sample take 3 half-life to decay from 3.6 x 10¹⁸ radioisotope atoms to 4.5 x 10¹⁷. Therefore, the time taken
t = 3T_½
t = 3(8) = 24h

Example 2

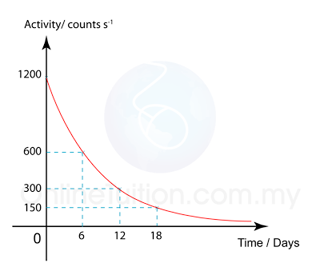
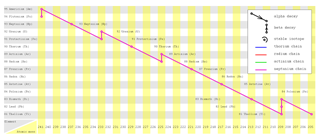
The diagram shows the graph of the activity of a radioisotope, X, against time. What is the half-life of the radioactive substance?

Answer:
The half-life is the time taken for the activity to decrease to become half of the initial value.

From the graph we can see that the radioisotope take 6 days for the activity to become half. Therefore

Half-life = 6 days

Alpha Decay

1. During an alpha decay, a radioactive atom X decay and emits an alpha particle ($He$ ).
2. Atom X losses 2 neutron and 2 proton and become atom Y.

Beta decay

1. A beta particles is an electron emitted from a nucleus.
2. The beta particles are very small and move with very high speed.
3. During a beta decay, a radioactive atom X decay and emits a beta particle ($e$ ).
4. One of the neutron is disintegrated to become proton and electron. The electron is emitted out from the nucleus whereas the proton stay in the nucleus.
   
5. Therefore proton number increase by 1 and the nucleon number remain unchanged.

Gamma Emission 

3 Types of Radioactive Emission

Alpha Particle

• carries positive charge.
• most strongly ionizing of the nuclear radiations. 
• least penetrating. Range in air is only a few centimetres, and can be stopped by a thick sheet of paper.

Beta Particle

• carry a negative charge. 
• much less ionizing than alpha emission.
• more penetrating than alpha emission..
• have a range of a metre or so in air,
• can be stopped by a few millimetres of Perspex or aluminium.

Gamma Radiation

• often emitted at the same time as an alpha or beta particle.
• least ionizing of the nuclear radiations, 
• most penetrating.
• their intensity is greatly reduced by several centimetres of lead, but they are never completely absorbed.

Ionising Effect

• All alpha, beta and gamma emission can cause ionising effect.
• Alpha particle has high ionizing power.Beta particle has low ionizing power.
• Gamma ray has very low ionizing power.

Penetrating Power

Deflection in Electric Field

Deflection in Magnetic Field

• Alpha and beta emission can be deflected by a magnetic field.
• The direction of deflection can be determined by using Fleming’s Left Hand Rule.
• Beta particle deflected more compare to alpha particle due to its much smaller mass.

Summary

Series Decay

1. Sometimes after a radioactive decay, the daughter nuclide formed is still unstable.
2. It will further decay into another nuclide which may also unstable.
3. This process continues until a stable nuclide is reached. This is called a series decay.
4. Each decay will emit either an alpha particle or a beta particle and may be gamma ray.
5. Figure below shows a series decay started from plutonium-241 to formed Thallium-205 eventually.

(This image is created by Johantheghost under creative common licence)

[Can detect: Alpha particles only]

1. Alpha radiation can be detected using a charged electroscope as in on the left. The more intense the radiation, the faster the leaf falls. 
2. The method isn't suitable for detecting beta and gamma-radiation as these cause insufficient ionization of the air.

1. All the α-particle, β-particle and γ-ray can be detected by a photograph film.
2. The ionisation effect by the radioactive rays will decompose silver bromide crystal on the film.
3. Films are kept in the badges worn by workers as a tracer device of radioactive rays.
4. The main disadvantages of using a film as a radioactive tracer is that it needs to be processed in order to prove the presence of radioactive rays)

[Can detect: Alpha particles only]

1. A spark-chamber detector is a particle detector, that is, a device used in particle physics for detecting electrically charged particles. 
2. Spark-chamber detectors consists of metal plates placed in a sealed box filled with gas (for example, helium, neon or a mixture of the two); as a particle travels through the detector, it will ionize the gas between the plates, and a trigger system is used to apply high voltage to the plates to create an electric field immediately after the particle went through the chamber, producing sparks on its exact trajectory.

[Can detect: Alpha, Beta and Gamma]

1. The tube contains argon gas at low pressure.
2. The end of the tube is sealed by a mica 'window' thin enough to allow alpha particles to pass into the tube as well as beta and gamma radiation.
3. When a charged particle or gamma-radiation enters the tube, the argon gas becomes ionized. This triggers a whole avalanche of ions between the electrodes. 
4. For a brief moment, the gas conducts and a pulse of current flows in the circuit. 
5. The circuit includes either a scaler or a ratemeter. A scaler counts the pulses and shows the total on a display. 
6. A ratemeter indicates the number of pulses or counts per second. The complete apparatus is often called a Geiger counter.

1. Most methods of detecting alpha-, beta- and gamma-rays are based on the fact that these radiations have an ionizing effect.
2. The detectors used to detect radioactive emissions include
   1. 3 Types of Radioactive Emission
   2. Characteristics of Radioactive Emission
3. Detectors of Radiation
   1. Gold Leaf Electroscope
   2. Geiger-Muller Tube
   3. Cloud Chamber
   4. Spark-Chamber Detector
   5. Film Badge (Dosimeter)
4. Table below shows the types of emission that can be detected by different detectors

Detectors	Alpha	Beta	Gamma
Gold Leaf Electroscope
Geiger-Muller Tube
Cloud Chamber
Spark-Chamber Detector
Film Badge (Dosimeter)

Isotopes

1. Isotopes are atoms of certain elements which have the same number of protons but different number of neutrons in the nucleus of the atoms.
2. It can also be defined as atoms of certain elements with the same proton numbers but with different nucleon numbers.
3. Isotopes have the same chemical properties but different physical properties.
4. Table below shows the proton and nucleon number of the isotopes of hydrogen and oxygen.

Radioactivity

1. Radioactivity is the spontaneous process of an unstable nucleus emitting radioactive emission in order to become more stable.
2. The process is said to be spontaneous because it is neither affected by the physical condition nor the chemical composition.
3. Decay is said to occur in the parent nucleus and produces a daughter nucleus. This is a random process, i.e. it is impossible to predict the decay of individual atoms.

Radioisotopes

Isotopes of an element that undergo radioacivity is called the radioisotopes.