[adinserter block="3"]
Question 1:
Diagram 1 shows an experiment to study the transmission of pressure in liquid by hydraulic system. A weight is added on the big piston’s syringe. The suitable weights are added on the small piston’s syringe until both pistons are at the same level. The weight added represents the force acting on both pistons.
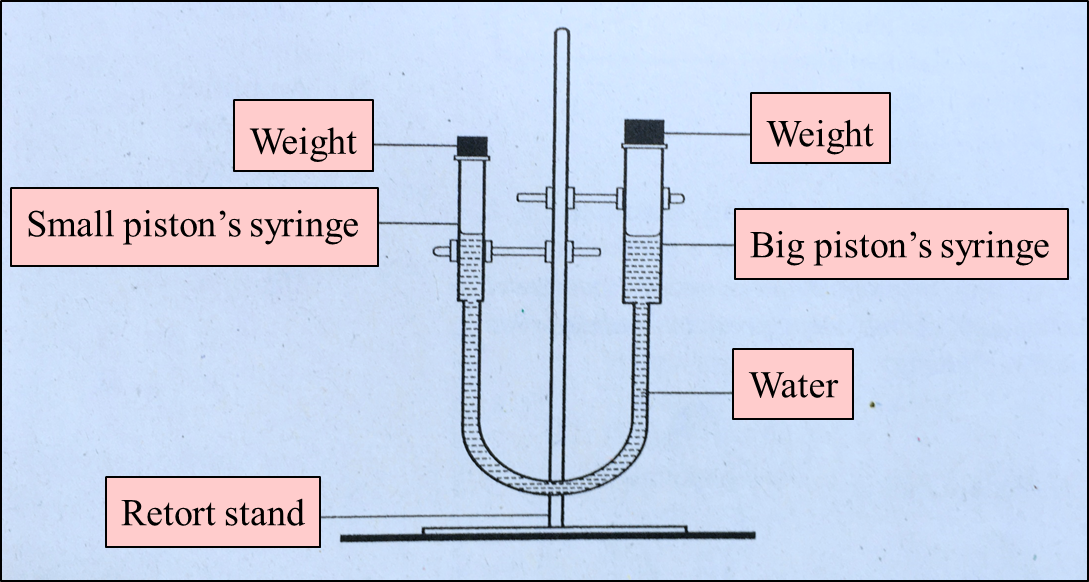 Diagram 1
Diagram 1
[adinserter block="3"]
The result of the experiment is shown in Table 1.
 Table 1
Table 1
[adinserter block="3"]
(a) Based on the result in Table 1, draw a graph to show the force acting on the small piston against the force acting on the big piston on the graph paper provided. [2 marks]
[adinserter block="3"]
(b) Based on the graph in 1(a), what is the force acting on the small piston if the force acting on the big piston is 8 N? [1 mark]
(c) What is the factor being fixed in this experiment? [1 mark]
(d) Name an appliance that uses the same principle as in Diagram 1. [1 mark]
[adinserter block="3"]
Answer:
(a)
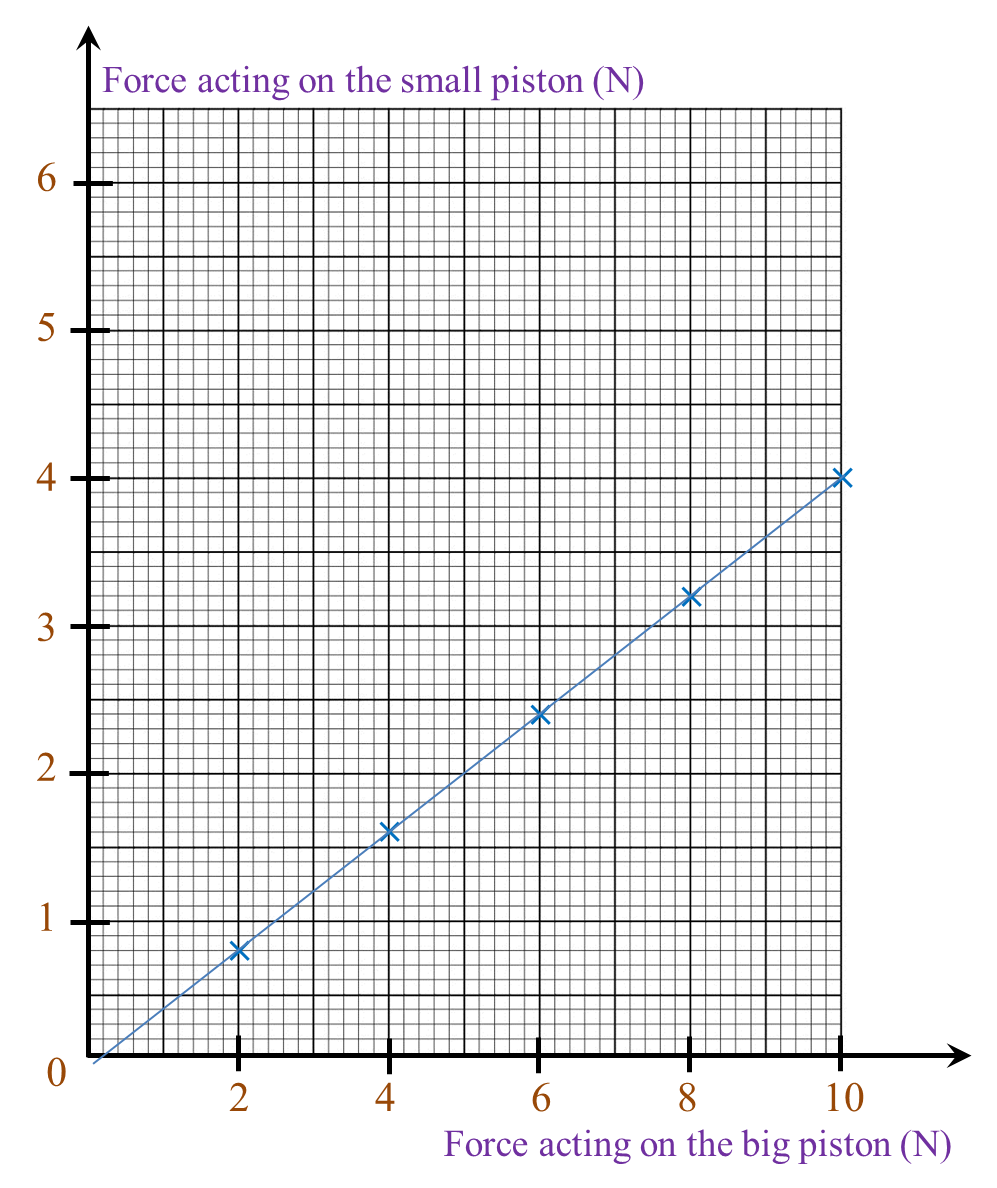
(b) 3.2 N (± 0.1)
(c) Volume of water
(d) Hydraulic brake / Hydraulic jack
Diagram 1 shows an experiment to study the transmission of pressure in liquid by hydraulic system. A weight is added on the big piston’s syringe. The suitable weights are added on the small piston’s syringe until both pistons are at the same level. The weight added represents the force acting on both pistons.
 Diagram 1
Diagram 1[adinserter block="3"]
The result of the experiment is shown in Table 1.
 Table 1
Table 1[adinserter block="3"]
(a) Based on the result in Table 1, draw a graph to show the force acting on the small piston against the force acting on the big piston on the graph paper provided. [2 marks]

[adinserter block="3"]
(b) Based on the graph in 1(a), what is the force acting on the small piston if the force acting on the big piston is 8 N? [1 mark]
(c) What is the factor being fixed in this experiment? [1 mark]
(d) Name an appliance that uses the same principle as in Diagram 1. [1 mark]
[adinserter block="3"]
Answer:
(a)

(b) 3.2 N (± 0.1)
(c) Volume of water
(d) Hydraulic brake / Hydraulic jack
[adinserter block="3"]
Question 2:
Diagram 2 shows an experiment to study the effect of light on the growth of bacteria.
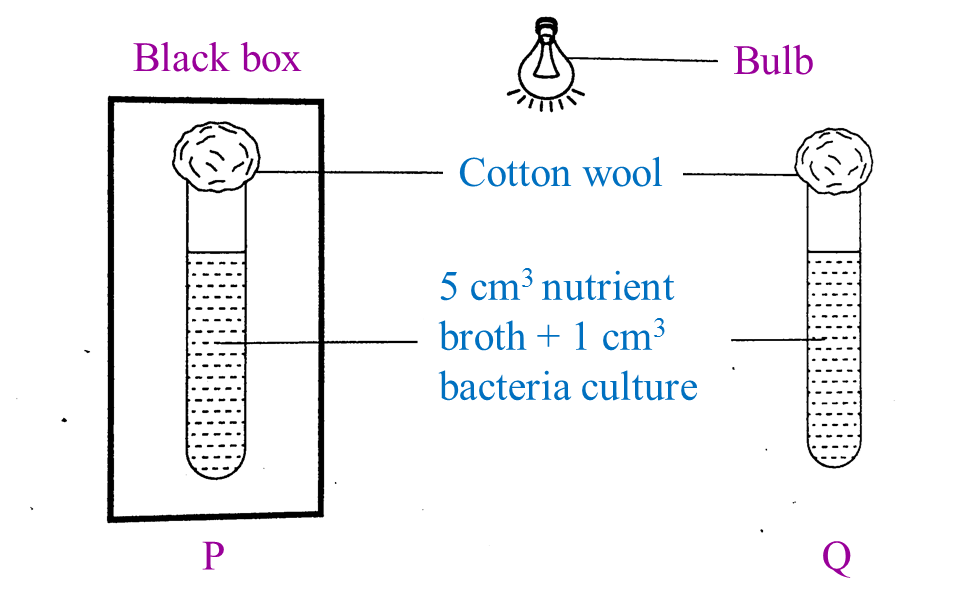 Diagram 2
Diagram 2
[adinserter block="3"]
The condition of the nutrient broth in test tube P and Q is observed after three days.
The result of this experiment is recorded in Table 2.
 Table 2
Table 2
[adinserter block="3"]
(a) State one observation on the nutrient broth which has been kept in the black box for three days. [1 mark]
(b) State one inference for this experiment. [1 mark]
(c) State the variables in this experiment. [2 marks]
(i) Manipulated variable
(ii) Responding variable
(d) Based on this experiment, state the operational definition of bacteria. [1 mark]
[adinserter block="3"]
Answer:
(a) Condition of nutrient broth is cloudy.
(b) The bacteria grow actively in dark condition.
(c)(i) Presence of light
(c)(ii) Condition of nutrient broth
(d) Bacteria is a microorganism that caused the condition of nutrient broth turns cloudy.
Diagram 2 shows an experiment to study the effect of light on the growth of bacteria.
 Diagram 2
Diagram 2[adinserter block="3"]
The condition of the nutrient broth in test tube P and Q is observed after three days.
The result of this experiment is recorded in Table 2.
 Table 2
Table 2[adinserter block="3"]
(a) State one observation on the nutrient broth which has been kept in the black box for three days. [1 mark]
(b) State one inference for this experiment. [1 mark]
(c) State the variables in this experiment. [2 marks]
(i) Manipulated variable
(ii) Responding variable
(d) Based on this experiment, state the operational definition of bacteria. [1 mark]
[adinserter block="3"]
Answer:
(a) Condition of nutrient broth is cloudy.
(b) The bacteria grow actively in dark condition.
(c)(i) Presence of light
(c)(ii) Condition of nutrient broth
(d) Bacteria is a microorganism that caused the condition of nutrient broth turns cloudy.
 (Speed is derived from dividing distance by time.)
(Speed is derived from dividing distance by time.)












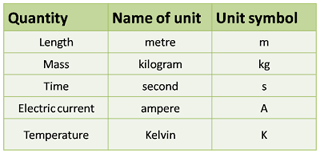 TIPS: In SPM, you MUST remember all 5 base quantities and its SI unit.
TIPS: In SPM, you MUST remember all 5 base quantities and its SI unit. 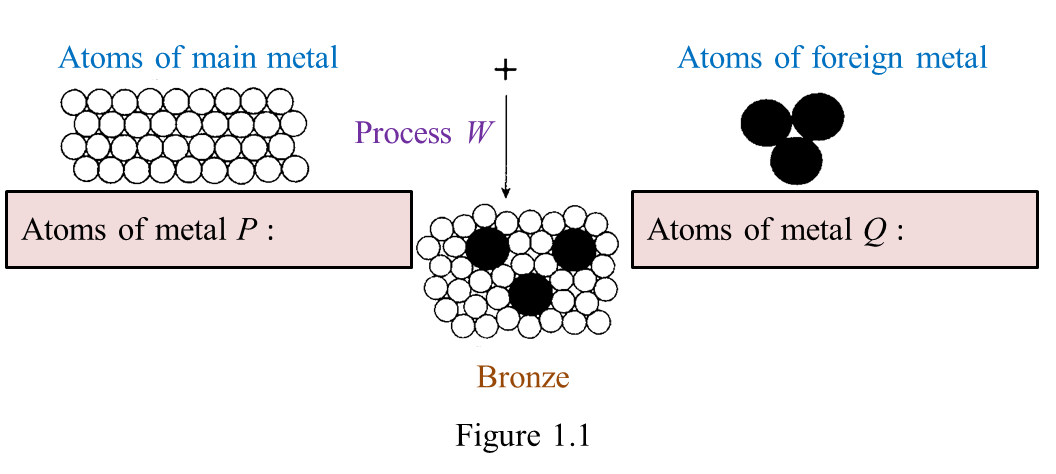
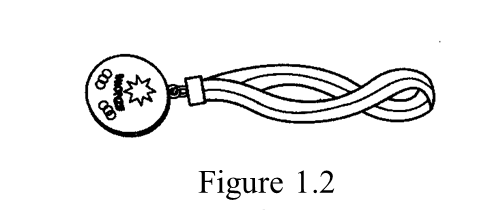 (d) The medal in Figure 1.2 is made of bronze.
(d) The medal in Figure 1.2 is made of bronze.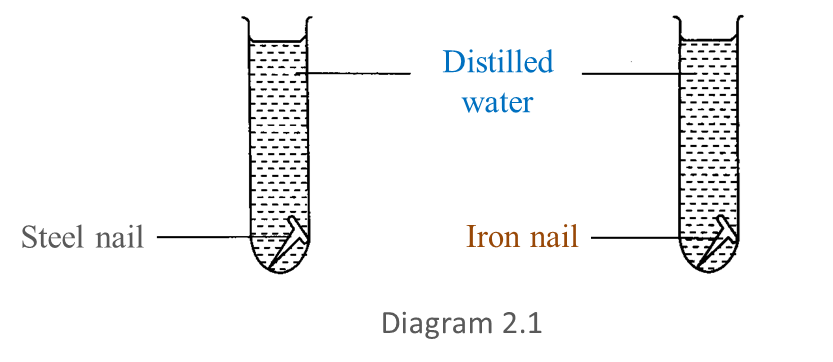
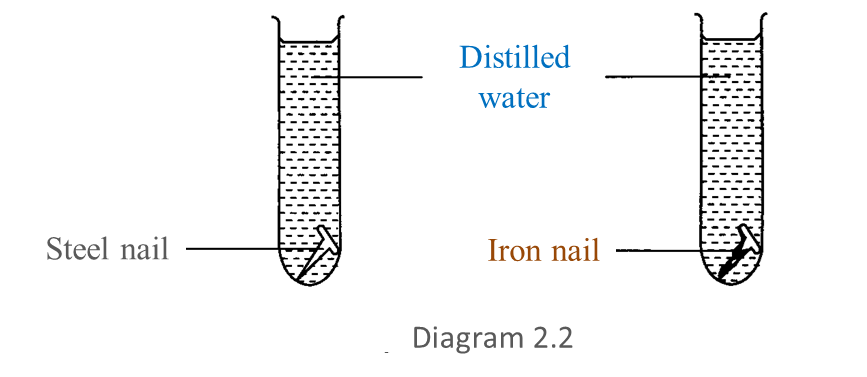
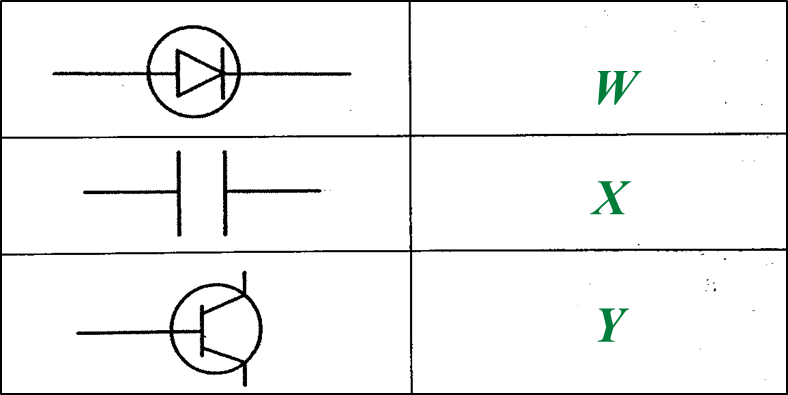 Diagram 1.1
Diagram 1.1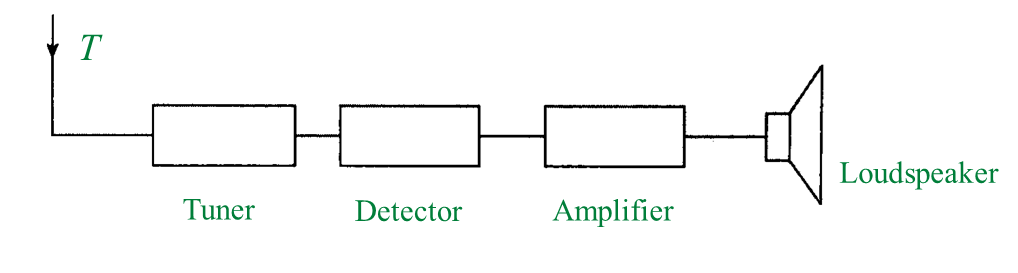 Diagram 1.2
Diagram 1.2 Diagram 1.3
Diagram 1.3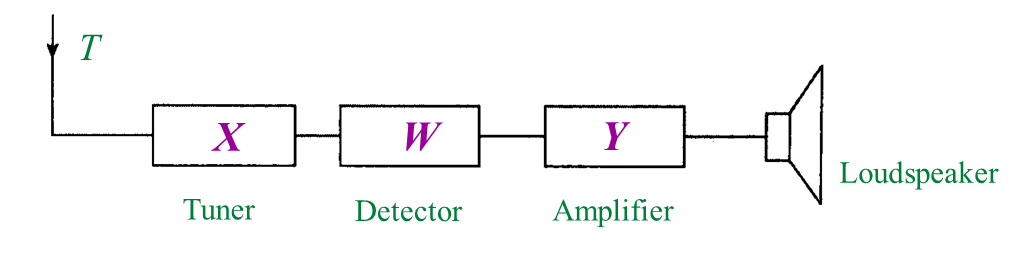

 Table 1
Table 1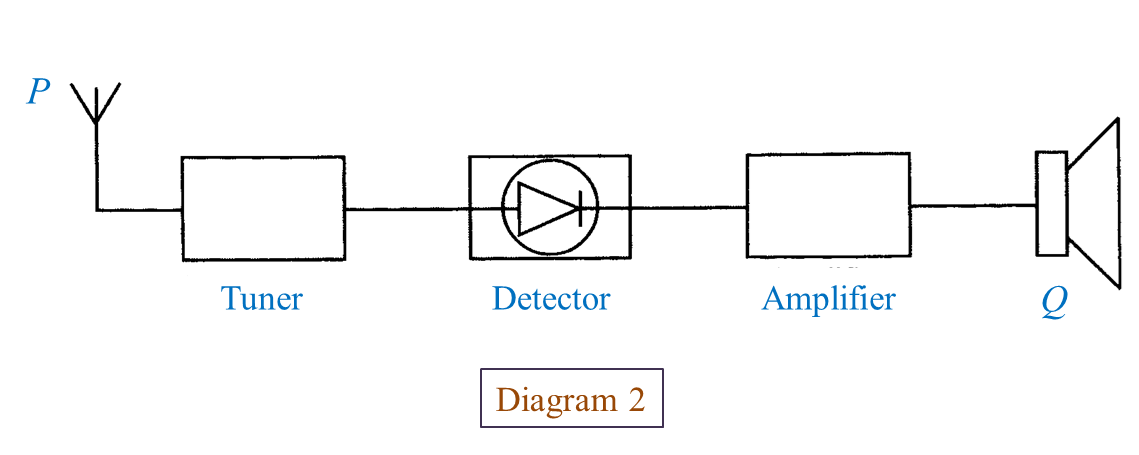 (b) What is the function of P? [1 mark]
(b) What is the function of P? [1 mark]