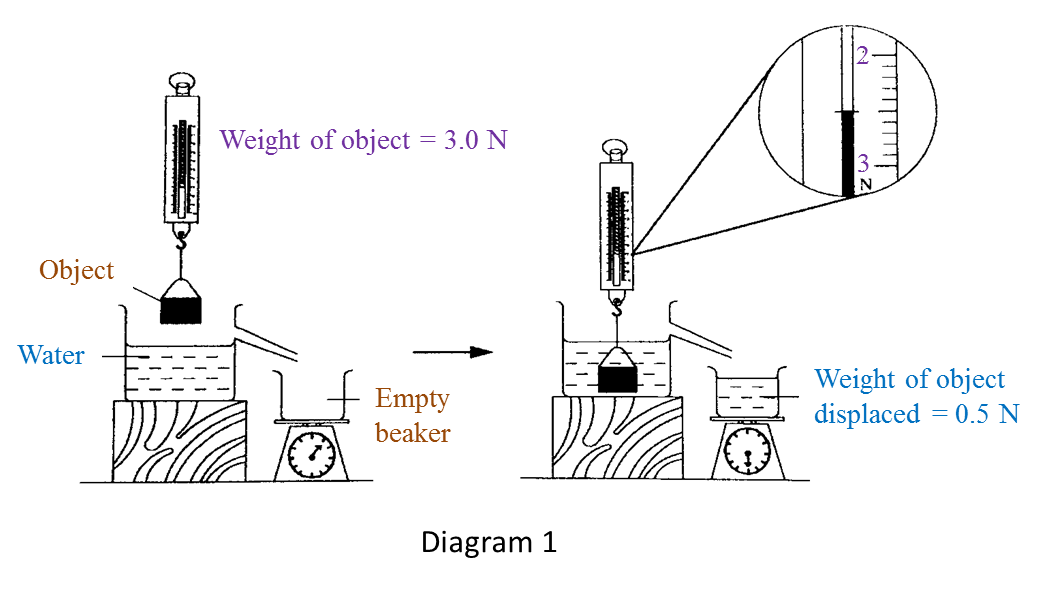
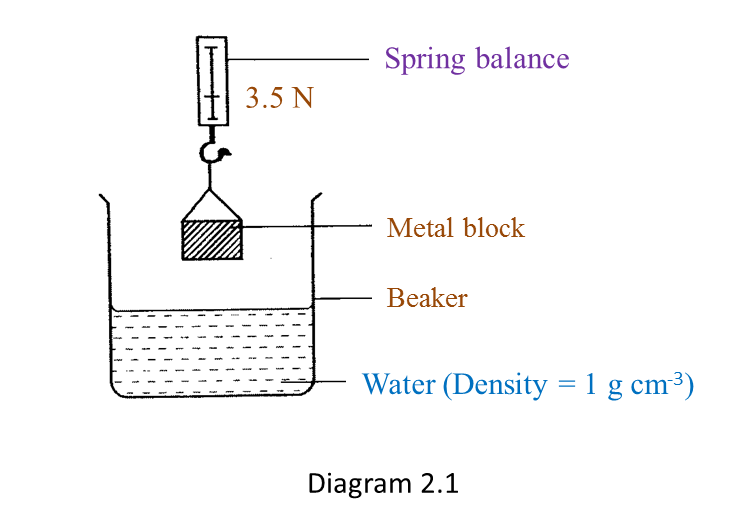
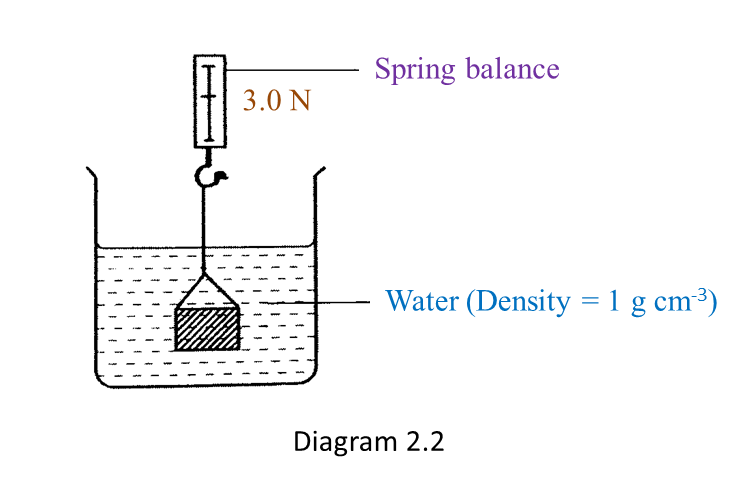
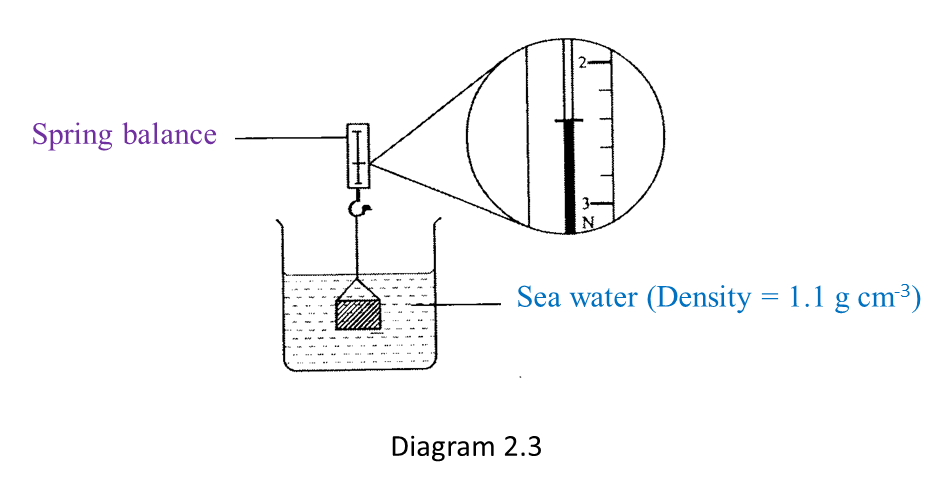
7.2.2 Algebraic Formulae, PT3 Practice

Posted on March 6, 2018 by user

Question 6:

Given 2 a b = 3 a - \frac{b^{2}}{2} . Express a in terms of b .

Solution:

\begin{array}{l} 2 a b = 3 a - \frac{b^{2}}{2} \\ 3 a - 2 a b = \frac{b^{2}}{2} \\ a (3 - 2 b) = \frac{b^{2}}{2} \\ a = \frac{b^{2}}{2 (3 - 2 b)} \end{array}

Question 7:

Given a = \frac{\sqrt{b + 1}}{a} . Express b in terms of a .

Solution:

\begin{array}{l} a = \frac{\sqrt{b + 1}}{a} \\ \sqrt{b + 1} = a^{2} \\ {[{(b + 1)}^{\frac{1}{2}}]}^{2} = {(a^{2})}^{2} \\ b + 1 = a^{4} \\ b = a^{4} - 1 \end{array}

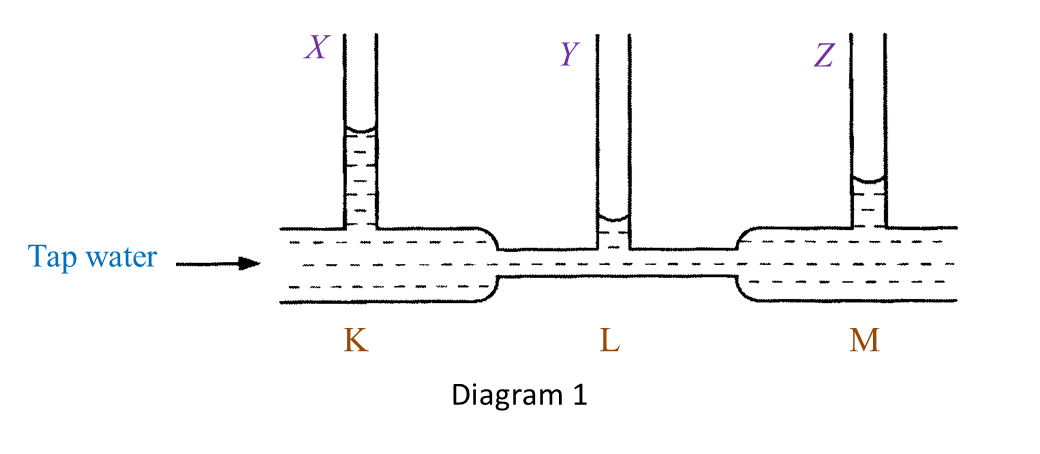
Question 8:

\begin{array}{l} Given x = \frac{5 w}{2 w - y} . \\ (i) Express w in terms of x and y . \\ (ii) Find the value of w when x = 10 and y = 15. \end{array}

Solution:

\begin{array}{l} (i) \\ x = \frac{5 w}{2 w - y} \\ 2 w x - x y = 5 w \\ 2 w x - 5 w = x y \\ w (2 x - 5) = x y \\ w = \frac{x y}{2 x - 5} \\ (ii) \\ w = \frac{(10) (15)}{2 (10) - 5} \\ = \frac{150}{15} \\ = 10 \end{array}

Question 9:
Azmin is h years old. His father is twice his brother’s age. If Azmin is 3 years older than his brother, write a formula for the sum (S) of their age.

Solution:
Azmin’s age = h
Azmin’s brother’s age = h – 3
Azmin’s father’s age = (h – 3) × 2 = 2h – 6

Therefore, the sum (S) of their age
S = h + (h – 3) + (2h – 6)
S = h + h – 3 + 2h – 6
S = 4h – 9

Question 10:
Mei Ling is 12 years older than Ali. In the next four years, Raju will be two times older than Ali. If h represents Ali’s age, write the algebraic expressions that represent the total of their ages, in terms of h, in four years time.

Solution:
Ali’s age in the next four years = h + 4
Mei Ling’s age = (h + 4) + 12 = h + 16
Raju’s age = (h + 4) × 2 = 2h + 8

Therefore, the total (S) of their age
S = (h + 4) + (h + 16) + (2h + 8)
S = 4h + 28

7.2.1 Algebraic Formulae, PT3 Practice

Posted on March 4, 2018 by user

7.2.1 Algebraic Formulae, PT3 Practice

Question 1:

Given m²+ 7 = k, express m in terms of k.

Solution:

\begin{array}{l} m^{2} + 7 = k \\ m^{2} = k - 7 \\ m = \sqrt{k - 7} \end{array}

Question 2:

Given 5km = mn – 2k, express k in terms of m and n.

Solution:

\begin{array}{l} 5 k m = m n - 2 k \\ 5 k m + 2 k = m n \\ k (5 m + 2) = m n \\ k = \frac{m n}{5 m + 2} \end{array}

Question 3:

Given

2 k - \frac{m}{2 n} = m

, express m in terms of k and n.

Solution:

\begin{array}{l} 2 k - \frac{m}{2 n} = m \\ - m - \frac{m}{2 n} = - 2 k \\ m + \frac{m}{2 n} = 2 k \\ \frac{2 n m + m}{2 n} = 2 k \\ \frac{m (2 n + 1)}{2 n} = 2 k \\ m = \frac{4 k n}{2 n + 1} \end{array}

Question 4:

Given

\frac{4 m}{\sqrt{T} - k} = \frac{3 h}{m}

, express T in terms of h and m.

Solution:

\begin{array}{l} \frac{4 m}{\sqrt{T} - k} = \frac{3 h}{m} \\ 4 m^{2} = 3 h \sqrt{T} - 3 h k \\ 3 h \sqrt{T} = 4 m^{2} + 3 h k \\ \sqrt{T} = \frac{4 m^{2} + 3 h k}{3 h} \\ T = {(\frac{4 m^{2} + 3 h k}{3 h})}^{2} \leftarrow Square both sides \end{array}

Question 5:

Given

\sqrt{\frac{8 s - 3 h}{4}} = 2

, express s in terms of h.

Solution:

\begin{array}{l} \sqrt{\frac{8 s - 3 h}{4}} = 2 \\ \frac{8 s - 3 h}{4} = 4 \leftarrow Square both sides \\ 8 s - 3 h = 16 \\ 8 s = 16 + 3 h \\ s = \frac{16 + 3 h}{8} \\ s = 2 + \frac{3 h}{8} \end{array}

7.1 Algebraic Formulae

Posted on March 1, 2018 by user

7.1 Algebraic Formulae

7.1.1 Variables and Constant

1. A variable is a quantity without a fixed value.

2. A constant is a quantity with a fixed value.

7.1.2 Concept of Formulae

1. An algebraic formula is an equation which shows the relationship between several variables and/ or constant.

2. The subject of an algebraic formula is a linear variable expressed in terms of the other variables.

Example 1:

Express x in terms of y, if y = \frac{2 - 3 x}{x} .

Solution:

\begin{array}{l} y = \frac{2 - 3 x}{x} \\ x y = 2 - 3 x \\ x y + 3 x = 2 \\ x (y + 3) = 2 \\ x = \frac{2}{y + 3} \end{array}

Example 2:

Given that s = \frac{p^{2} - q^{2}}{2 u}, make p the subject of the formula .

Solution:

\begin{array}{l} s = \frac{p^{2} - q^{2}}{2 r} \\ 2 r s = p^{2} - q^{2} \\ p^{2} = 2 r s + q^{2} \\ p = \sqrt{2 r s + q^{2}} \end{array}

6.2.3 Algebraic Expressions (III), PT3 Practice

Posted on February 23, 2018 by user

Question 11:
(a)
Expand: x (2 + y)

(b)

\begin{array}{l} Express \frac{5}{6 y} - \frac{3 x - 5}{12 y} as a single \\ fraction in its simplest form . \end{array}

Solution:
(a)
x (2 + y) = 2x + xy

(b)

\begin{array}{l} \frac{5}{6 y} - \frac{3 x - 5}{12 y} \\ = \frac{5 \times 2}{6 y \times 2} - \frac{3 x - 5}{12 y} \\ = \frac{10 - (3 x - 5)}{12 y} \\ = \frac{10 - 3 x + 5}{12 y} \\ = \frac{15 - 3 x}{12 y} \\ = \frac{3 (5 - x)}{12^{4} y} \\ = \frac{5 - x}{4 y} \end{array}

6.2.2 Algebraic Expressions (III), PT3 Practice

Posted on February 22, 2018 by user

6.2.2 Algebraic Expressions (III), PT3 Practice

Question 6:
(a) Simplify each of the following:

\begin{array}{l} (i) \frac{12 m n}{32} \\ (ii) \frac{x^{2} - x y}{x} \end{array}

(b) Express

\frac{1}{2 q} - \frac{2 p - 7}{6 q}

as a single fraction in its simplest form.

Solution:

\begin{array}{l} (a)(i) \frac{12 m n}{32} = \frac{3 m n}{8} \\ (a)(ii) \frac{x^{2} - x y}{x} = \frac{x (x - y)}{x} = x - y \end{array}

(b)

\begin{array}{l} \frac{1}{2 q} - \frac{2 p - 7}{6 q} = \frac{1 \times 3}{2 q \times 3} - \frac{(2 p - 7)}{6 q} \\ = \frac{3 - 2 p + 7}{6 q} \\ = \frac{10 - 2 p}{6 q} \\ = \frac{2 (5 - p)}{36 q} \\ = \frac{5 - p}{3 q} \end{array}

Question 7:

(a) Factorise 2ae + 3af – 6de – 9df

(b) Simplify

\frac{a^{2} - b^{2}}{{(a + b)}^{2}}

Solution:

(a)

2ae + 3af – 6de – 9df = a (2e + 3f ) – 3d (2e + 3f)

= (2e + 3f ) (a – 3d)

(b)

\begin{array}{l} \frac{a^{2} - b^{2}}{{(a + b)}^{2}} = \frac{(a + b) (a - b)}{(a + b) (a + b)} \\ = \frac{a - b}{a + b} \end{array}

Question 8:

(a) Factorise –8c² – 12ac.

(b) Simplify

\frac{a e + a d - 2 b e - 2 b d}{a^{2} - 4 b^{2}} .

Solution:

(a)

–8c²– 12ac

= –4c (2c + 3a)

(b)

\begin{array}{l} \frac{a e + a d - 2 b e - 2 b d}{a^{2} - 4 b^{2}} = \frac{a (e + d) - 2 b (e + d)}{(a + 2 b) (a - 2 b)} \\ = \frac{(e + d) (a - 2 b)}{(a + 2 b) (a - 2 b)} \\ = \frac{e + d}{a + 2 b} \end{array}

Question 9:

(a) Factorise 12x² – 27y²

(b) Simplify

\frac{3 m^{2} - 10 m + 3}{m^{2} - 9} \div \frac{3 m - 1}{m + 3} .

Solution:

(a)

12x²– 27y²= 3 (4x² – 9y²)

= 3(2x – 3y) (2x + 3y)

(b)

\begin{array}{l} \frac{3 m^{2} - 10 m + 3}{m^{2} - 9} \div \frac{3 m - 1}{m + 3} = \frac{(3 m - 1) (m - 3)}{(m + 3) (m - 3)} \times \frac{m + 3}{3 m - 1} \\ = 1 \end{array}

Question 10:

Simplify: \frac{8 m + m n}{3 m} \div \frac{n^{2} - 64}{24}

Solution:

\begin{array}{l} \frac{8 m + m n}{3 m} \div \frac{n^{2} - 64}{24} \\ = \frac{8 m + m n}{3 m} \times \frac{24}{n^{2} - 64} \\ = \frac{m (8 + n)}{3 m} \times \frac{24}{n^{2} - 8^{2}} \\ = \frac{m (8 + n)}{3 m} \times \frac{24_{8}}{(n - 8) (n + 8)} \\ = \frac{8}{n - 8} \end{array}

5.7.4 The Motion of Vehicles in the Air (Structured Questions)

Posted on February 20, 2018 by user

Question 1:
Diagram 1 shows an experiment to study Bernoulli’s Principle.

(a)(i) State one observation of the water level in Diagram 1. [1 mark]

(ii) State one inference that can be made based on the observation in (a)(i). [1 mark]

(b) State the responding variable in this experiment. [1 mark]

(c) Based on this experiment, state the operational definition for Bernoulli’s Principle. [1 mark]

(d) Mark (\/) in the boxes provided to show the apparatus where the Bernoulli’s Principle is applied. [1 mark]

Answer:
(a)(i)
- The water level in the vertical tube Y is the lowest.
- The water level in the vertical tube X is the highest.
(any one)

(a)(ii)
- The water at the base of the vertical tube Y exerts the lowest pressure.
- The water at the base of the vertical tube X exerts the highest pressure.
(any one)

(b) The pressure exerted by the moving water.

(c) Bernoulli’s Principle states that pressure in a liquid decreases when the speed of the liquid increases.

(d)

6.2.1 Algebraic Expressions (III), PT3 Practice

Posted on February 20, 2018 by user

6.2.1 Algebraic Expressions (III), PT3 Practice

Question 1:

(a)(i) Factorise 18a + 3

(a)(ii) Expand –3 (–y + 5)

(b) Express

\frac{5}{6 y} - \frac{3 x - 5}{12 y}

as a single fraction in its simplest form.

Solution:

(a)(i) 18a + 3 = 3(6a + 1)

(a)(ii) –3 (–y + 5) = 3y – 15

(b)

\begin{array}{l} \frac{5}{6 y} - \frac{3 x - 5}{12 y} = \frac{5 \times 2}{6 y \times 2} - \frac{(3 x - 5)}{12 y} \\ = \frac{10 - 3 x + 5}{12 y} \\ = \frac{15 - 3 x}{12 y} \\ = \frac{3 (5 - x)}{412 y} \\ = \frac{5 - x}{4 y} \end{array}

Question 2:

(a) Expand:

(i) 3 (–a + c)

(ii) –5 (a – c)

(b) Factorise 4x + 2

\frac{3 x + 6}{x^{2} - 4} \div \frac{x + 2}{x - 2}

Solution:

(a)(i) 3 (–a + c) = –3a + 3c

(a)(ii) –5 (a – c) = –5a + 5c

(c)

\begin{array}{l} \frac{3 x + 6}{x^{2} - 4} \div \frac{x + 2}{x - 2} = \frac{3 (x + 2)}{(x + 2) (x - 2)} \times \frac{x - 2}{x + 2} \\ = \frac{3}{x + 2} \end{array}

Question 3:

(a) Factorise:

(i) 5m + 25

(ii) 7x + 9xy

(b) Simplify:

\frac{4 x - 12}{4 y} \div \frac{x^{2} - 9}{y z}

Solution:

(a)(i)5m + 25 = 5 (m + 5)

(a)(ii)7x + 9xy = x (7 + 9y)

\begin{array}{l} (b) \frac{4 x - 12}{4 y} \div \frac{x^{2} - 9}{y z} = \frac{4 (x - 3)}{4 y} \times \frac{y z}{(x + 3) (x - 3)} \\ = \frac{z}{x + 3} \end{array}

Question 4:

(a) Factorise completely:

4 – 100n²

(b) Express

\frac{4}{5 x} - \frac{7 - 10 y}{15 x}

as a single fraction in its simplest form.

Solution:

(a)

4 – 100n²= (2 + 10n)(2 – 10n)

(b)

\begin{array}{l} \frac{4}{5 x} - \frac{7 - 10 y}{15 x} = \frac{4 \times 3}{5 x \times 3} - \frac{(7 - 10 y)}{15 x} \\ = \frac{12 - 7 + 10 y}{15 x} \\ = \frac{5 + 10 y}{15 x} \\ = \frac{5 (1 + 2 y)}{315 x} \\ = \frac{1 + 2 y}{3 x} \end{array}

Question 5:

(a) Simplify:

(m – 4n)(m + 4n) – m²

(b) Simplify:

\frac{3 x - 3 y}{x + y} \times \frac{2 x + 2 y}{6 x}

Solution:

(a)

(m – 4n)(m + 4n) – m²

= m²+ 4mn – 4mn – 4n² – m²

= 0

(b)

\begin{array}{l} \frac{3 x - 3 y}{x + y} \times \frac{2 x + 2 y}{6 x} = \frac{3 (x - y)}{x + y} \times \frac{2 (x + y)}{6 x} \\ = \frac{x - y}{x} \end{array}

5.7.3 The Motion of Vehicles in Water (Structured Questions)

Posted on February 16, 2018 by user

Question 1:
Diagram 1 shows an experiment to study the relationship between upthrust and the weight of water displaced.

(a) Based on Diagram 1, state the weight of object in water and write down your answer in the Table below. [1 mark]

(b) Observe Diagram 1. Compare the weight of object in the air and in water. [1 mark]

(c) State one inference for this experiment. [1 mark]

(d) State one responding variable in this experiment. [1 mark]

(e) The upthrust acts on an object when it is immersed in water.
State the operational definition of upthrust. [1 mark]

Answer:
(a)

(b) The weight of object in the air is larger than the weight of object in the water.

(c) The apparent loss in weight is equal to the weight of water displaced.

(d) Weight of water displaced.

(e) Upthrust is the apparent loss in weight of an object when it is immersed in water.

Question 2:
Diagram 2.1 shows the weight of a metal block in the air.

Diagram 2.2 shows the apparent weight of the metal block when it is immersed in water.

(a) Based on Diagram 2.1 and Diagram 2.2:
(i) State one observation from the result of this experiment. [1 mark]

(ii) State one inference from this experiment. [1 mark]

(b) State the constant variable in this experiment. [1 mark]

The experiment is repeated by using sea water as shown in Diagram 2.3.

(c) Based on Diagram 2.3, what is the reading on the spring balance? [1 mark]

(d) Predict the reading of the spring balance if the metal block is immersed in a liquid which has higher density than sea water. [1 mark]

Answer:
(a)(i)
The weight of the metal block in air is larger than the apparent weight of the same metal block immersed in water.

(a)(ii)
An upthrust acts on the metal block when it is immersed in water.

(b) Metal block, water (density = 1 g cm^-3). (any one)

(c) 2.4 N

(d) The reading of the spring balance will be lower than the reading shown in Diagram 2.3.

6.1 Algebraic Expressions III

Posted on February 15, 2018 by user

6.1 Algebraic Expressions III

6.1.1 Expansion

1. The product of an algebraic term and an algebraic expression:

a(b + c) = ab + ac
a(b – c) = ab – ac

2. The product of an algebraic expression and another algebraic expression:

(a + b) (c + d) = ac + ad + bc + bd
(a + b)²= a² + 2ab + b²
(a – b)²= a² – 2ab + b²
(a + b) (a – b) = a² – b²

6.1.2 Factorization

1. Factorize algebraic expressions:

ab + ac = a(b + c)
a²– b²= (a + b) (a – b)
a²+ 2ab + b²= (a + b)²
ac + ad + bc + bd = (a + b) (c + d)

2. Algebraic fractions are fractions where both the numerator and the denominator or either the numerator or the denominator are algebraic terms or algebraic expressions.

Example:

\frac{3}{b}, \frac{a}{7}, \frac{a + b}{a}, \frac{b}{a - b}, \frac{a - b}{c + d}

3(a) Simplification of algebraic fractions by using common factors:

\begin{array}{l} • \frac{^{1} 4 b c}{^{_{^{3}}} 12 b d} = \frac{c}{3 d} \\ • \frac{b m + b n}{e m + e n} = \frac{b (m + n)}{e (m + n)} \\ = \frac{b}{e} \end{array}

3(b) Simplification of algebraic fractions by using difference of two squares:

\begin{array}{l} \frac{a^{2} - b^{2}}{a n + b n} = \frac{(a + b) (a - b)}{n (a + b)} \\ = \frac{a - b}{n} \end{array}

6.1.3 Addition and Subtraction of Algebraic Fractions

1. If they have a common denominator:

\frac{a}{m} + \frac{b}{m} = \frac{a + b}{m}

2. If they do not have a common denominator:

\frac{a}{m} + \frac{b}{n} = \frac{a n + b m}{n m}

6.1.4 Multiplication and Division of Algebraic Fractions

1. Without simplification:

\begin{array}{l} • \frac{a}{m} \times \frac{b}{n} = \frac{a b}{m n} \\ • \frac{a}{m} \div \frac{b}{n} = \frac{a}{m} \times \frac{n}{b} \\ = \frac{a n}{b m} \end{array}

2. With simplification:

\begin{array}{l} • \frac{a}{c m} \times \frac{b m}{d} = \frac{a b}{c d} \\ • \frac{a}{c m} \div \frac{b}{d m} = \frac{a}{c m} \times \frac{d m}{b} \\ = \frac{a d}{b c} \end{array}

5.2.3 Indices, PT3 Practice

Posted on February 9, 2018 by user

Question 13:

Solve: 3^{2 n + 1} = \frac{3^{n} \times 9}{{(9^{\frac{1}{2}})}^{- 3}}

Solution:

\begin{array}{l} 3^{2 n + 1} = \frac{3^{n} \times 9}{{(9^{\frac{1}{2}})}^{- 3}} \\ 3^{2 n + 1} = \frac{3^{n} \times 3^{2}}{3^{- 3}} \\ 3^{2 n + 1} = 3^{n + 2 - (- 3)} \\ 2 n + 1 = n + 5 \\ n = 4 \end{array}

Question 14:

Given that k^{3} = 9^{- \frac{3}{2}} \times 64^{\frac{1}{2}}, find the value of k .

Solution:

\begin{array}{l} k^{3} = 9^{- \frac{3}{2}} \times 64^{\frac{1}{2}} \\ = {(3^{2})}^{- \frac{3}{2}} \times {(2^{6})}^{\frac{1}{2}} \\ = 3^{- 3} \times 2^{3} \\ = {(\frac{2}{3})}^{3} \\ k = \frac{2}{3} \end{array}

Question 15:

{Given 9}^{x + 2} \div 3^{4} = 3^{x + 1}, calculate the value of x .

Solution:

\begin{array}{l} 9^{x + 2} \div 3^{4} = 3^{x + 1} \\ {(3^{2})}^{x + 2} \div 3^{4} = 3^{x + 1} \\ 3^{2 x + 4} \div 3^{4} = 3^{x + 1} \\ 2 x + 4 - 4 = x + 1 \\ 2 x = x + 1 \\ x = 1 \end{array}

Question 16:

Simplify: {(\frac{- 2 x^{5} y^{- 2}}{z^{\frac{1}{6}}})}^{3} \div \frac{1}{\sqrt{x^{2} z}}

Solution:

\begin{array}{l} {(\frac{- 2 x^{5} y^{- 2}}{z^{\frac{1}{6}}})}^{3} \div \frac{1}{\sqrt{x^{2} z}} \\ = \frac{- 8 x^{15} y^{- 6}}{z^{\frac{1}{2}}} \times \sqrt{x^{2} z} \\ = \frac{- 8 x^{15} y^{- 6}}{z^{\frac{1}{2}}} \times {(x^{2} z)}^{\frac{1}{2}} \\ = \frac{- 8 x^{15} y^{- 6}}{z^{\frac{1}{2}}} \times x z^{\frac{1}{2}} \\ = - 8 x^{15 + 1} y^{- 6} \\ = \frac{- 8 x^{16}}{y^{6}} \end{array}

Question 17:

Find the value of the following.

(a) (2³)²× 2⁴÷ 2⁵

(b)

\frac{a^{2} \times a^{\frac{1}{2}}}{{(a^{\frac{2}{3}} \times a^{\frac{1}{3}})}^{- 2}}

Solution:

(a)

(2³)²× 2⁴÷ 2⁵= 2⁶× 2⁴÷ 2⁵

= 2^6+4-5

= 2⁵

= 32

(b)

\begin{array}{l} \frac{a^{2} \times a^{\frac{1}{2}}}{{(a^{\frac{2}{3}} \times a^{\frac{1}{3}})}^{- 2}} = \frac{a^{2 + \frac{1}{2}}}{{(a^{\frac{2}{3}} \times a^{\frac{1}{3}})}^{- 2}} \\ = \frac{a^{2 + \frac{1}{2}}}{{(a^{\frac{2}{3} + \frac{1}{3}})}^{- 2}} \\ = \frac{a^{\frac{5}{2}}}{a^{- 2}} \\ = a^{\frac{5}{2} - (- 2)} \\ = a^{\frac{5}{2} + \frac{4}{2}} \\ = a^{\frac{9}{2}} \end{array}