Soalan 3:
(a) Jadual di bawah menunjukkan nilai-nilai x dan y bagi persamaan y = –x3 + 3x + 1.

Hitung nilai r dan nilai s.
(b) Untuk ceraian soalan ini, gunakan kertas graf. Anda boleh menggunakan pembaris fleksibel.
Dengan menggunakan skala 2cm kepada 1 unit pada paksi-x dan 2 cm kepada 5 unit pada paksi-y, lukis graf y = –x3 + 3x + 1 for –3 ≤ x ≤ 4 dan –51 ≤ y ≤ 19.
(c) Daripada graf anda, cari
(i) nilai y apabila x = –2.8,
(ii) nilai x apabila y = –30.
(i) nilai y apabila x = –2.8,
(ii) nilai x apabila y = –30.
(d) Lukis satu garis lurus yang sesuai pada graf anda untuk mencari nilai-nilai x yang memuaskan persamaan –x3 + 13x – 9 = 0 bagi –3 ≤ x ≤ 4 dan –51 ≤ y ≤ 19.
Penyelesaian:
(a)
y = –x3 + 3x + 1
apabila x = –1,
r = – (–1)3 + 3(–1) + 1
= 1 – 3 + 1 = –1
apabila x = 3,
s = – (3)3 + 3(3) + 1 = –17
(b)
(c)
(i) Dari graf, apabila x = –2.8, y = 15
(ii) Dari graf, apabila y = –30, x = 3.5
(d)
y = –x3 + 3x + 1 ----- (1)
–x3+ 13x – 9 = 0 ----- (2)
y = –x3 + 3x + 1 ----- (1)
0 = –x3 + 13x – 9 ------ (2) ← (Menyusun semula (2))
(1) – (2) : y = –10x + 10
Garis lurus yang sesuai ialah y = –10x + 10.
Menentukan koordinat-x bagi titik-titik persilangan antara lengkungan y = –x3 + 3x + 1 dan garis lurus y = –10x + 10.
x |
0 |
4 |
y = –10x + 10 |
10 |
–30
|
Dari graf, x = 0.7, 3.25.
Soalan 4:
(a) Lengkapkan jadual di ruang jawapan bagi persamaan y = x3 – 4x – 10 dengan menulis nilai-nilai y apabila x = –1 dan x = 3.
(b) Untuk ceraian soalan ini, gunakan kertas graf. Anda boleh menggunakan pembaris fleksibel.
Dengan menggunakan skala 2cm kepada 1 unit pada paksi-x dan 2 cm kepada 10 unit pada paksi-y, lukis graf y = x3 – 4x – 10 untuk –3 ≤ x ≤ 4 dan –25 ≤ y ≤ 38.
(c) Dari graf, cari,
(i) nilai y apabila x = 2.2,
(ii) nilai x apabila y = 15.
(d) Lukis satu garis lurus yang sesuai pada graf anda untuk mencari nilai-nilai x yang memuaskan persamaan x3 – 12x – 5 = 0 untuk –3 ≤ x ≤ 4 dan –25 ≤ y ≤ 38.
Jawapan:

Penyelesaian:
(a)
y = x3 – 4x – 10
Apabila x = –1,
y = (–1)3 – 4(–1) – 10
= –7
Apabila x = 3,
y = (3)3 – 4(3) – 10
= 5
(b)
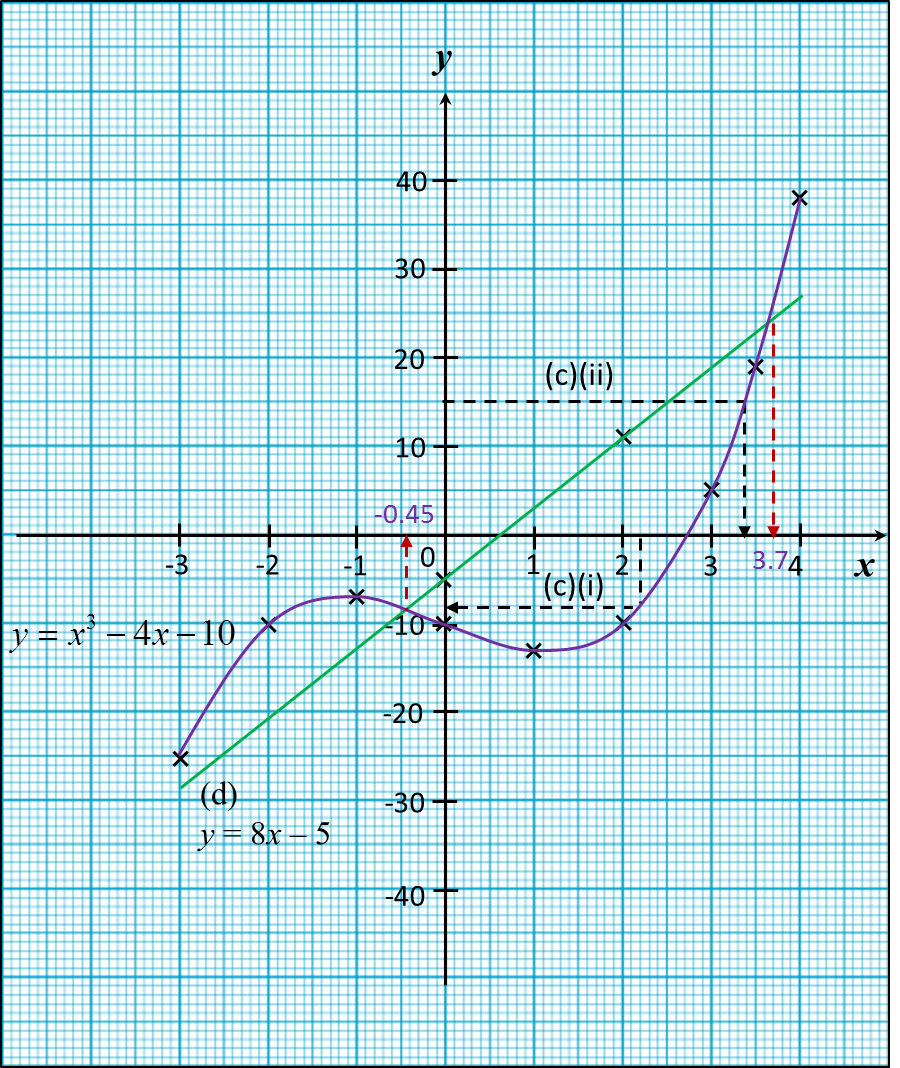
(c)
(i) Dari graf, apabila x = 2.2, y = –8
(ii) Dari graf, apabila y = 15, x = 3.4
(d)
y = x3 – 4x – 10 ----- (1)
0 = x3 – 12x – 5 ----- (2)
(1) – (2) : y = 8x – 5
Garis lurus yang sesuai ialah y = 8x–5.
Menentukan koordinat-x bagi titik-titik persilangan antara lengkungan y = x3 – 4x – 10 dan garis lurus y = 8x –5.
Dari graf, x = –0.45, 3.7.
(a) Lengkapkan jadual di ruang jawapan bagi persamaan y = x3 – 4x – 10 dengan menulis nilai-nilai y apabila x = –1 dan x = 3.
(b) Untuk ceraian soalan ini, gunakan kertas graf. Anda boleh menggunakan pembaris fleksibel.
Dengan menggunakan skala 2cm kepada 1 unit pada paksi-x dan 2 cm kepada 10 unit pada paksi-y, lukis graf y = x3 – 4x – 10 untuk –3 ≤ x ≤ 4 dan –25 ≤ y ≤ 38.
(c) Dari graf, cari,
(i) nilai y apabila x = 2.2,
(ii) nilai x apabila y = 15.
(d) Lukis satu garis lurus yang sesuai pada graf anda untuk mencari nilai-nilai x yang memuaskan persamaan x3 – 12x – 5 = 0 untuk –3 ≤ x ≤ 4 dan –25 ≤ y ≤ 38.
Jawapan:

Penyelesaian:
(a)
y = x3 – 4x – 10
Apabila x = –1,
y = (–1)3 – 4(–1) – 10
= –7
Apabila x = 3,
y = (3)3 – 4(3) – 10
= 5
(b)

(c)
(i) Dari graf, apabila x = 2.2, y = –8
(ii) Dari graf, apabila y = 15, x = 3.4
(d)
y = x3 – 4x – 10 ----- (1)
0 = x3 – 12x – 5 ----- (2)
(1) – (2) : y = 8x – 5
Garis lurus yang sesuai ialah y = 8x–5.
Menentukan koordinat-x bagi titik-titik persilangan antara lengkungan y = x3 – 4x – 10 dan garis lurus y = 8x –5.
x |
0 |
2 |
y = 8x – 5 |
–5 |
–11
|
