Question 5:
In diagram below, PQUV is a square, QRTU is a rectangle and RST is an equilateral triangle.
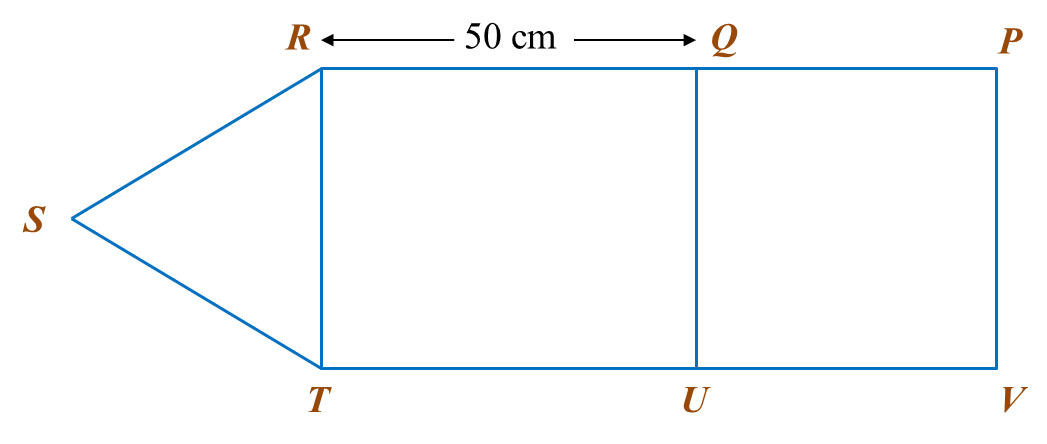
The perimeter of the whole diagram is 310 cm.
Calculate the length, in cm, of PV.
Solution:
In diagram below, PQUV is a square, QRTU is a rectangle and RST is an equilateral triangle.

The perimeter of the whole diagram is 310 cm.
Calculate the length, in cm, of PV.
Solution:
Question 6:
In diagram below, ABCD and CGFE are rectangles. M, G, E and N are midpoints of AB, BC, CD and DA respectively.
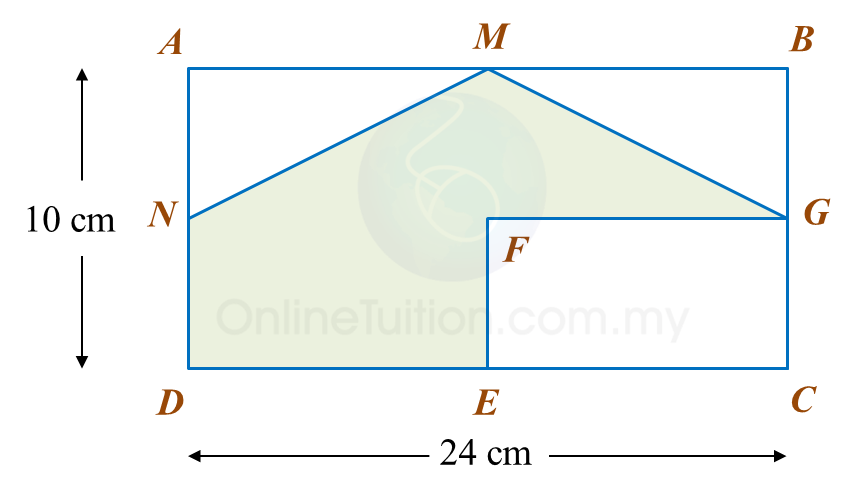
Calculate the perimeter, in cm, of the coloured region.
Solution:
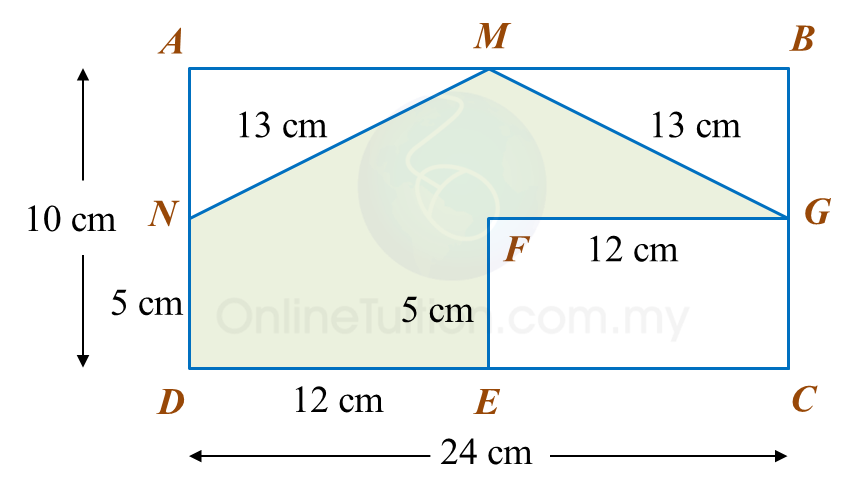
In diagram below, ABCD and CGFE are rectangles. M, G, E and N are midpoints of AB, BC, CD and DA respectively.

Calculate the perimeter, in cm, of the coloured region.
Solution:

Question 7:
Diagram below shows a trapezium BCDE and a parallelogram ABEF. ABC and FED are straight lines.
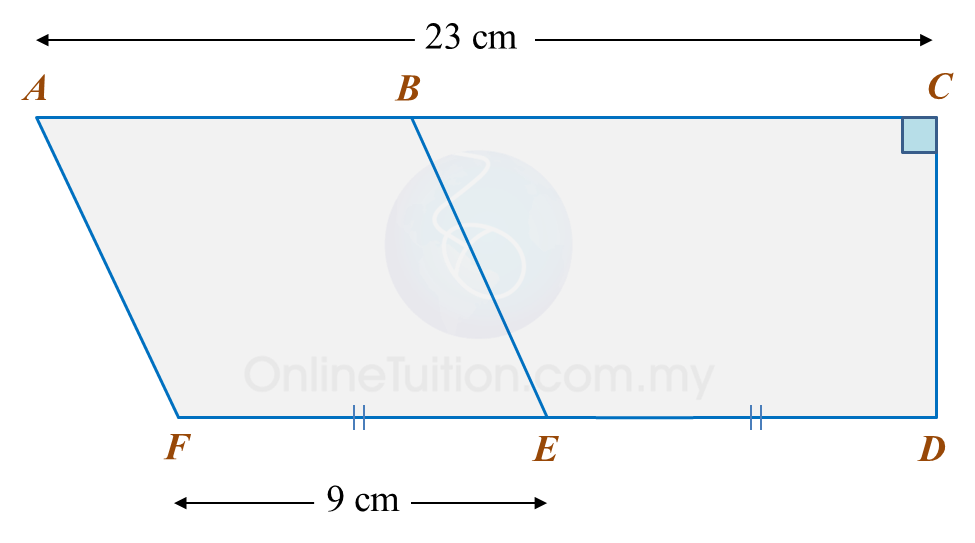 The area of ABEF is 72 cm2.
The area of ABEF is 72 cm2.
Calculate the area, in cm2, of trapezium BCDE.
Solution:
Diagram below shows a trapezium BCDE and a parallelogram ABEF. ABC and FED are straight lines.
 The area of ABEF is 72 cm2.
The area of ABEF is 72 cm2.Calculate the area, in cm2, of trapezium BCDE.
Solution:
Question 8:
In diagram below, ACEF is a trapezium and BCDG is a square.
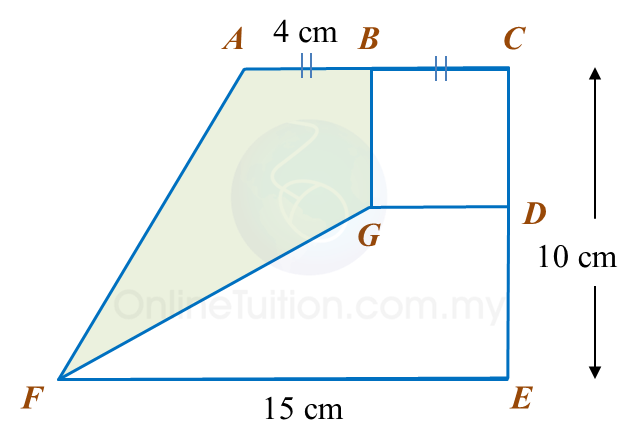
Calculate the area, in cm2, of the coloured region.
Solution:
In diagram below, ACEF is a trapezium and BCDG is a square.

Calculate the area, in cm2, of the coloured region.
Solution: