Question 9:
In diagram below, ADB is a right-angled triangle and DBFE is a square. C is the midpoint of DB and CH = CD.
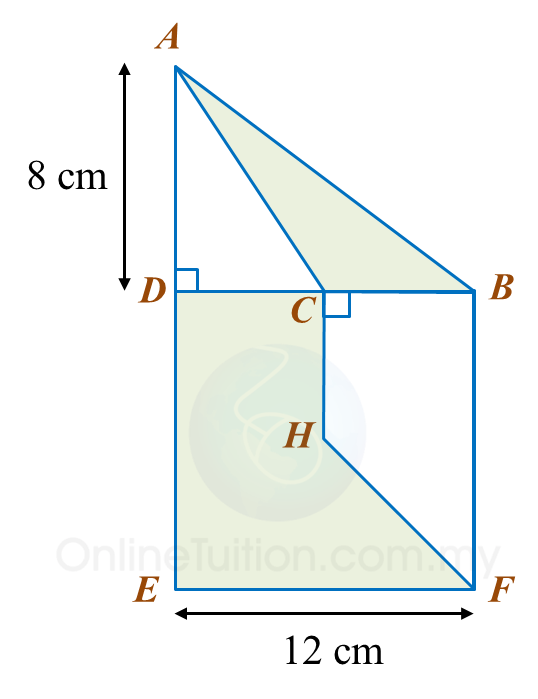 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.
Solution:
In diagram below, ADB is a right-angled triangle and DBFE is a square. C is the midpoint of DB and CH = CD.
 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.Solution:
Question 10:
Diagram below shows a rectangle ACDE.
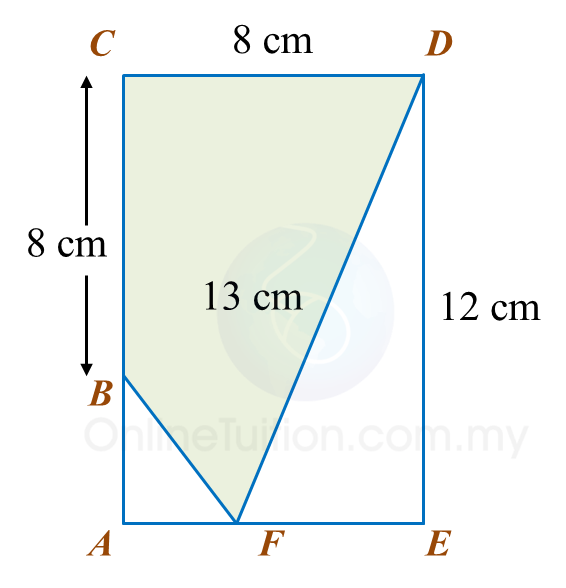
Calculate the area, in cm2, of the coloured region.
Solution:
Diagram below shows a rectangle ACDE.

Calculate the area, in cm2, of the coloured region.
Solution:
Question 11:
Diagram below shows a sketch of parallelogram shaped garden, PQRS that consists of flower beds and a playground.
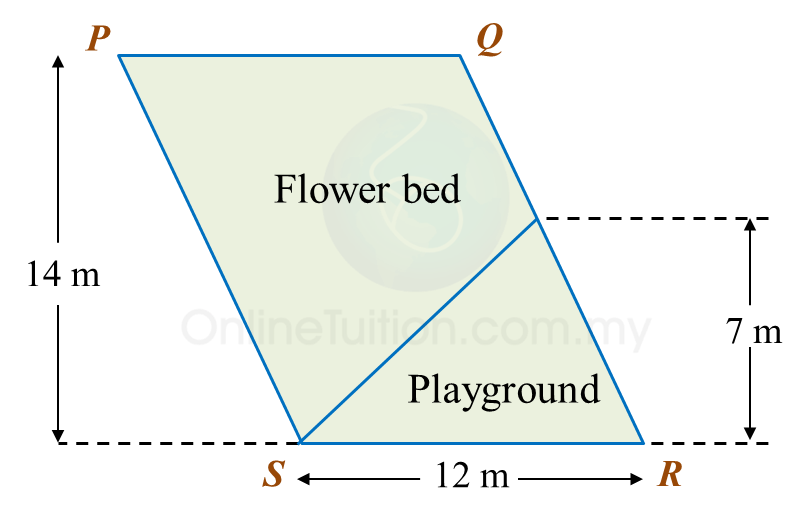 Calculate the area, in m2, of the flower beds.
Calculate the area, in m2, of the flower beds.
Solution:
Diagram below shows a sketch of parallelogram shaped garden, PQRS that consists of flower beds and a playground.
 Calculate the area, in m2, of the flower beds.
Calculate the area, in m2, of the flower beds.Solution: