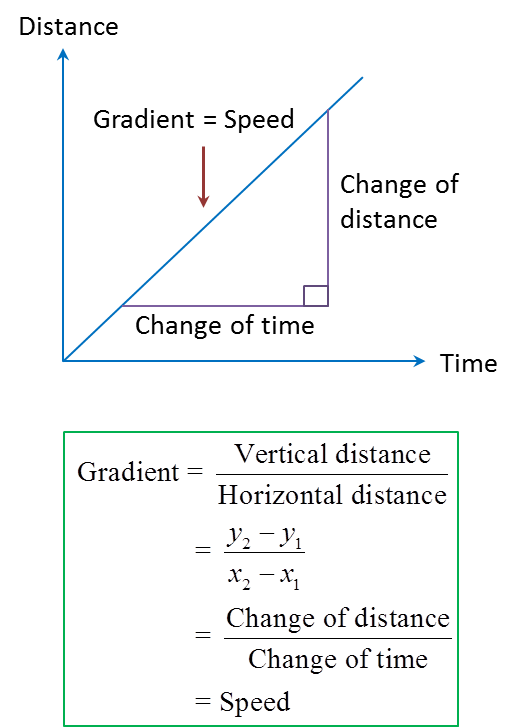
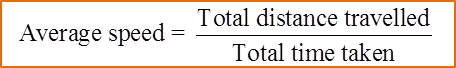(B) Speed – Time Graph
1. The gradient of a speed-time graph is the rate of change of speed or acceleration.


2.
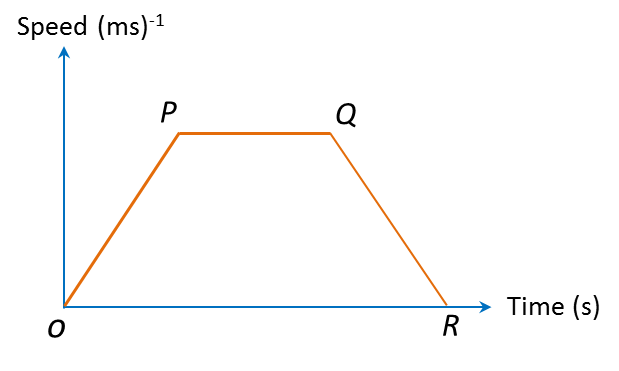

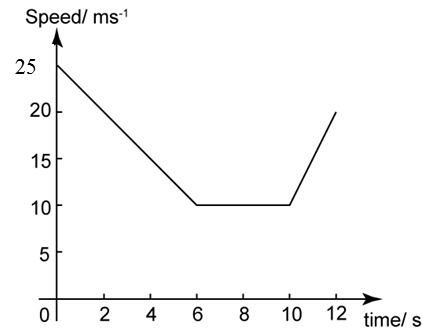
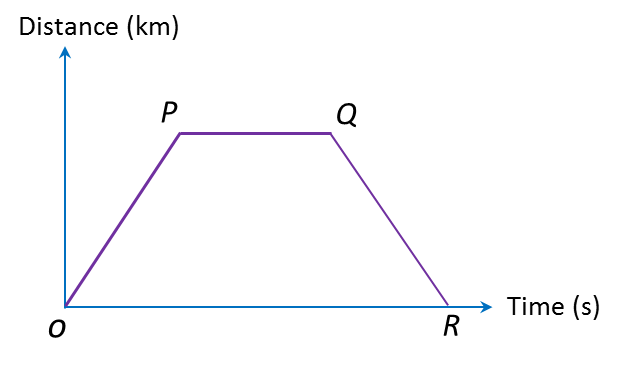
(a) From O to P: Gradient = positive → (Speed of object increasing or accelerating).
(b) From P to Q: Gradient = 0 → (Object is moving at uniform speed).
(c) From Q to R: Gradient = negative → (Speed of object decreasing or decelerating).
Example:
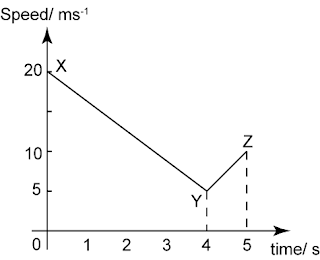

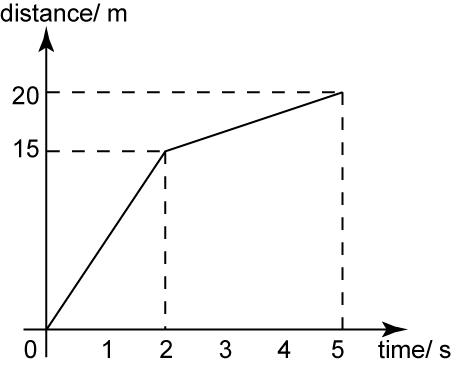
The diagram above shows the speed-time graph of a moving car for 5 seconds. Find
(a) the rate of speed change when the car travel from X to Y.
(b) the rate of speed change when the car travel from Y to Z.
Solution:
(a)
Rate of speed change when the car travels from X to Y
= Gradient
(b)
Rate of speed change when the car travels from Y to Z
= Gradient