4.3 Operasi ke atas Pernyataan (Bhg 3)
(C) Nilai Kebenaran Pernyataan Gabungan yang menggunakan Perkataan ‘Atau’
1. Gabungan dua pernyataan dengan perkataan ‘atau’ menghasilkan satu pernyataan baru yang
(a) palsu, apabila kedua-dua pernyataan yang digabungkan itu adalah palsu,
(b) benar, apabila salah satu atau kedua-dua pernyataan yang digabungkan itu benar.
(a) palsu, apabila kedua-dua pernyataan yang digabungkan itu adalah palsu,
(b) benar, apabila salah satu atau kedua-dua pernyataan yang digabungkan itu benar.
Jadual kebenaran:
Katakan p = pernyataan 1 dan q = pernyataan 2.
Nilai kebenaran bagi ‘p’ dan ‘q’ adalah seperti berikut:
p |
q |
p atau q (pernyataan gabungan) |
Benar |
Benar |
Benar |
Benar |
Palsu |
Benar |
Palsu |
Benar |
Benar |
Palsu |
Palsu |
Palsu |
Contoh 6:
Tentukan nilai kebenaran bagi setiap pernyataan berikut:
(a) 60 boleh dibahagi dengan 4 atau 9.
(b) 53 = 25 atau 43 = 64.
(c) 5 + 7 > 14 atau √9 = 2.
Penyelesaian:
(a)
60 boleh dibahagi dengan 4 ← (p adalah benar)
60 boleh dibahagi dengan 9 ← (q adalah palsu)
Oleh itu, 60 boleh dibahagi dengan 4 atau 9 adalah satu pernyataan benar. (‘p atau q’ adalah benar)
(b)
53 = 25 ← (q adalah palsu)
43 = 64 ← (q adalah benar)
Oleh itu, 53 = 25 atau 43 = 64 adalah satu pernyataan benar. (‘p atau q’ adalah benar)
(c)
5 + 7 > 14 ← (p adalah palsu)
√9 = 2 ← (q adalah palsu)
Oleh itu, 5 + 7 > 14 atau √9 = 2 adalah satu pernyataan palsu. (‘p atau q’ adalah palsu)
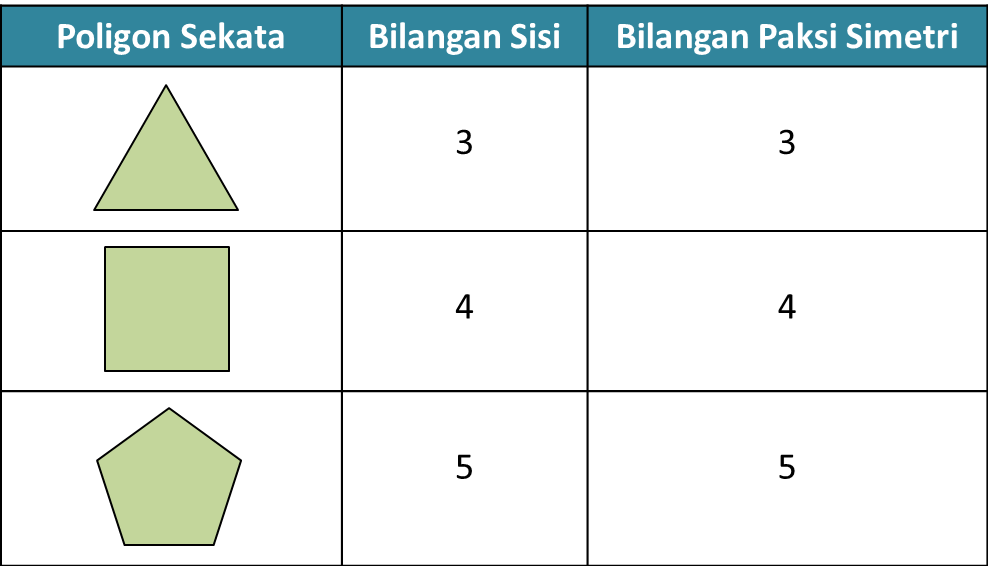 Jadual 1
Jadual 1 Rajah 7
Rajah 7

