7.4 SPM Practice (Short Questions)

Posted on April 24, 2020 by user

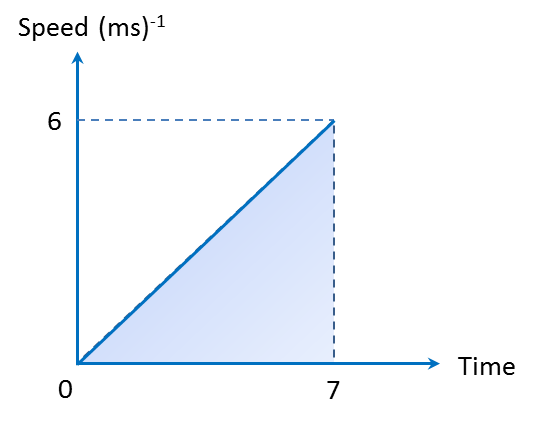
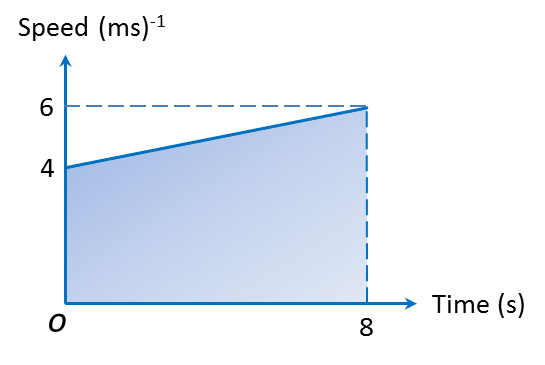
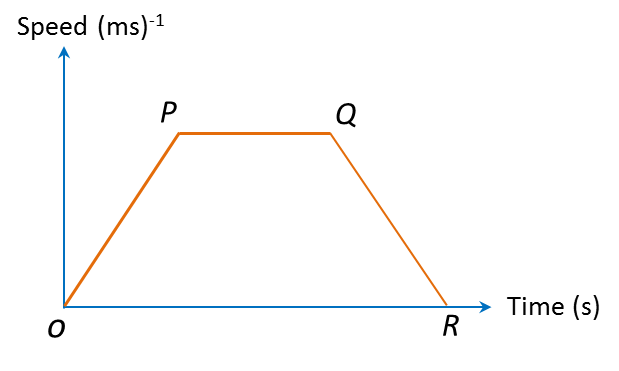
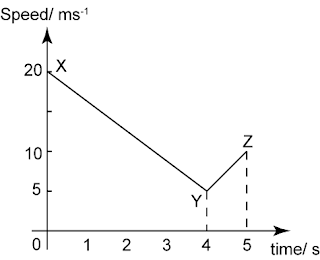
Question 1:
A bag contains 36 marbles which are black and white. It is given that the probability for a black marble being picked at random from the bag is

\frac{5}{9}

.
Calculate the number of white marbles to be taken out from the bag so that the probability of picking a black marble is

\frac{5}{8}

Solution:

\begin{array}{l} Number of black marbles in the bag \\ = \frac{5}{9} \times 36 = 20 \\ Let y is the total number of marbles left in the bag . \\ y \times \frac{5}{8} = 20 \\ y = 20 \times \frac{8}{5} = 32 \\ Number of white marbles to be taken out from the bag \\ = 36 - 32 \\ = 4 \end{array}

Question 2:

Table below shows the number of different coloured balls in three bags.

	Green	Brown	Purple
Bag A	3	1	6
Bag B	5	3	4
Bag C	4	6	2

If a bag is picked at random and then a ball is drawn randomly from that bag, what is the probability that a purple ball is drawn?

Solution:
Probability of picking a bag =

\frac{1}{3}

Probability of picking purple ball from bag A =

\frac{6}{10} = \frac{3}{5}

Probability of picking purple ball from bag B =

\frac{4}{12} = \frac{1}{3}

Probability of picking purple ball from bag C =

\frac{2}{12} = \frac{1}{6}

\begin{array}{l} P (purple ball) = (\frac{1}{3} \times \frac{3}{5}) + (\frac{1}{3} \times \frac{1}{3}) + (\frac{1}{3} \times \frac{1}{6}) \\ = \frac{1}{5} + \frac{1}{9} + \frac{1}{18} \\ = \frac{11}{30} \end{array}

Question 3:
A box contains 48 marbles. There are red marbles and green marbles. A marble is chosen at random from the box. The probability that a red marble is chosen is

\frac{1}{6} .

How many red marbles need to be added to the box so that the probability that a red marble is chosen is

\frac{1}{2} .

Solution:

\begin{array}{l} Number of red marbles in the box \\ = \frac{1}{6} \times 48 \\ = 8 \\ Let the number of red marbles needed to be added be y . \\ P (red marble) = \frac{1}{2} \\ \frac{8 + y}{48 + y} = \frac{1}{2} \\ 16 + 2 y = 48 + y \\ 2 y - y = 48 - 16 \\ y = 32 \\ ∴ Number of red marbles need to be added = 32 \end{array}

7.3 Probability of a Combined Event

Posted on April 24, 2020 by user

7.3 Probability of a Combined Event

7.3b Finding the Probability of Combined Events (a) A or B (b) A and B

1. The probability of a combined event ‘A or B’ is given by the formula below.

\begin{array}{l} P (A or B) = P (A \cup B) \\ = \frac{n (A \cup B)}{n (S)} \end{array}

2. The probability of a combined event ‘A and B’ is given by the formula below.

\begin{array}{l} P (A and B) = P (A \cap B) \\ = \frac{n (A \cap B)}{n (S)} \end{array}

Example:

The probabilities that two Form 5 students, Fiona and Wendy will pass the English oral test are

\frac{1}{3} and \frac{2}{5}

respectively. Calculate the probability that

(a) both Fiona and Wendy past the English oral test,
(b) both Fiona and Wendy fail the English oral test,

(c) either one of them passes the English oral test,
(d) at least one of them passes the English oral test.

Solution:

Let

F = Event that Fiona passes the English oral test

W = Event that Wendy passes the English oral test

Therefore,

F’ = Event that Fiona fails the English oral test

W’ = Event that Wendy fails the English oral test

\begin{array}{l} P (F) = \frac{1}{3}, P (F') = \frac{2}{3} \\ P (W) = \frac{2}{5}, P (W') = \frac{3}{5} \end{array}

(a)

P (both Fiona and Wendy past the English oral test)

= P (F ∩ W)

= P (F) x P (W)

\begin{array}{l} = \frac{1}{3} \times \frac{2}{5} \\ = \frac{2}{15} \end{array}

(b)

P (both Fiona and Wendy fail the English oral test)

= P (F’ ∩ W’)
= P (F’) x P (W’)

\begin{array}{l} = \frac{2}{3} \times \frac{3}{5} \\ = \frac{2}{5} \end{array}

(c)

P (either one of them passes the English oral test)

= P (F ∩ W’) + P (F’ ∩ W)
= (P (F) x P (W’)) + (P (F’) x P (W))

\begin{array}{l} = (\frac{1}{3} \times \frac{3}{5}) + (\frac{2}{3} \times \frac{2}{5}) \\ = \frac{7}{15} \end{array}

(d)

P (at least one of them passes the English oral test)

= 1 – P (Both of them fail) ← (concept of complement event)

= 1 – P (F’) x P (W’)

\begin{array}{l} = 1 - \frac{2}{5} \\ = \frac{3}{5} \end{array}

7.3 Probability of a Combined Event

Posted on April 24, 2020 by user

7.3 Probability of a Combined Event

7.3a Finding the Probability of a Combined Event by Listing the Outcomes

1. A combined event is an event resulting from the union or intersection of two or more events.

2. The union of combined event ‘A or B’ = A υ B

3. The intersection of combined event ‘A and B’ = A ∩ B

Example:

Diagram below shows five cards labelled with letters.

All these cards are put into a box. A two-letter code is to be formed by using any two of these cards. Two cards are picked at random, one after another, without replacement.

(a) List all sample space

(b) List all the outcomes of the events and find the probability that

(i) The code begins with the letter P.

(ii) The code consists of two vowel or two consonants.

Solution:

(a)

Sample space, S

= {(G, R), (G, A), (G, P), (G, E), (R, G), (R, A), (R, P), (R, E), (A, G), (A, R),

(A, P), (A, E), (P, G), (P, R), (P, A), (P, E), (E, G), (E, R), (E, A), (E, P)}

(b)

n(S) = 20

Let

A = Event of choosing a code begins with the letter P

B = Event of choosing the code consists of two vowel or two consonants.

(i)

A = {(P, G), (P, R), (P, A), (P, E)}

n(A) = 4

P (A) = \frac{4}{20} = \frac{1}{5}

(ii)

B = {(G, R), (G, P), (R, G), (R, P), (A, E), (P, G), (P, R), (E, A)}

n(B) = 8

P (B) = \frac{8}{20} = \frac{2}{5}

7.5 SPM Practice (Long Questions)

Posted on April 24, 2020 by user

Question 1:

All the cards written with the letters from the word ‘INTERNATIONAL’ are put into a box.

Two cards are drawn at random from the box, one after another, without replacement. Calculate the probability that

(a) the first card drawn has a letter N and the second card drawn has a letter I.

(b) the two cards drawn have the same letter.

Solution:
(a)
There are three cards with the letter ‘N’ and two card with letter ‘I’.
P (the first card drawn has a letter N and the second card drawn has a letter I)

\begin{array}{l} = \frac{3}{13} \times \frac{2}{(13 - 1)} \\ = \frac{3}{13} \times \frac{2}{12} = \frac{1}{26} \end{array}

(b)
P (the two cards drawn have the same letter)
= P (II or NN or TT or AA)
= P (II) + P (NN) + P (TT) + P (AA)

\begin{array}{l} = (\frac{2}{13} \times \frac{1}{12}) + (\frac{3}{13} \times \frac{2}{12}) + (\frac{2}{13} \times \frac{1}{12}) + (\frac{2}{13} \times \frac{1}{12}) \\ ↑ \\ \begin{array}{l} There are 3 letter ' N' \\ out of 13 letters \end{array} \\ = \frac{2}{156} + \frac{6}{156} + \frac{2}{156} + \frac{2}{156} \\ = \frac{12}{156} \\ = \frac{1}{13} \end{array}

Question 2:
During National Day celebration, a group of 8 boys and 5 girls from a school are taking part in a singing competition. Each day, two pupils are chosen at random to perform special skill.

(a) Calculate the probability that both pupils chosen to perform special skill are boys.

(b) Two boys were chosen to perform special skill on the first day. They are exempted from performing special skill on the second day.
Calculate the probability that both pupils chosen to perform special skill on the second day are of the same gender.

Solution:
(a)

\begin{array}{l} P (both pupils are boys) \\ = P (B B) \\ = \frac{8}{13} \times \frac{7}{12} \\ = \frac{7}{24} \end{array}

(b)

\begin{array}{l} P (both pupils are of the same gender) \\ = P (B B) + P (G G) \\ = (\frac{6}{11} \times \frac{5}{10}) + (\frac{5}{11} \times \frac{4}{10}) \leftarrow \begin{array}{l} 11 pupils left in the group to \\ perform special skill on the second \\ day after two boys were exempted . \end{array} \\ = \frac{3}{11} + \frac{2}{11} \\ = \frac{5}{11} \end{array}

7.1 Probability of an Event

Posted on April 24, 2020 by user

7.1 Probability of an Event

The probability of an event A, P(A) is given by

\begin{array}{l} P (A) = \frac{Number of times event A occurs}{Number of trials} \\ P (A) = \frac{n (A)}{n (S)} \\ where 0 \leq P (A) \leq 1 \end{array}

If P(A) = 0, then the event A will certainly not occur.

If P(A) = 1, then the event A is sure to occur.

Example 1:

A box contains 9 red pens and 13 blue pens. Tom puts another 4 red pens and 2 blue pens into the box. A pen is picked at random from the box. What is the probability that a red pen is picked?

Solution:

n(S) = 9 + 13 + 4 + 2 = 28

Let A = Event that a red pen is picked

n(A) = 9 + 4 = 13

\begin{array}{l} P (A) = \frac{n (A)}{n (S)} \\ = \frac{13}{28} \end{array}

Example 2:

A bag contains 45 green cards and yellow cards. A card is picked at random from the bag. The probability that a green card is picked is

\frac{1}{5} .

How many green cards must be added to the bag so that the probability of picking a green card becomes ½?

Solution:

n(S) = 45

Let

x = number of green cards in the bag.

A = Event of randomly picking a green card.

n(A) = x

\begin{array}{l} P (A) = \frac{n (A)}{n (S)} \\ \frac{1}{5} = \frac{x}{45} \\ x = \frac{45}{5} \\ x = 9 \end{array}

Let y is the number of green cards added to the bag.

\frac{9 + y}{45 + y} = \frac{1}{2}

2 (9 + y) = 45 + y

18 + 2y= 45 + y

2y – y = 45 – 18

y = 27

6.2 Quantity Represented by the Area under a Graph (Part 1)

Posted on April 24, 2020 by user

6.2 Quantity Represented by the Area under a Graph (Part 1)

1. In the speed-time graph,

(a) Quantity represented by the gradient of the graph is acceleration or the rate of change of speed.

(b) Quantity represented by the area under the graph is distance.

Example 1:

Calculate the distance of each of the following graphs.

(a)

Distance = Area under the speed-time graph = Area of a triangle

\begin{array}{l} Distance = \frac{1}{2} \times b a s e \times h e i g h t \\ = \frac{1}{2} \times 7 \times 6 = 21 m \end{array}

(b)

Distance = Area under the speed-time graph = Area of a rectangle

Distance = Length × Breadth

= 6 × 4 = 24 m

(c)

Distance = Area under the speed-time graph = Area of a trapezium

\begin{array}{l} Distance = \frac{1}{2} (a + b) h \leftarrow \begin{array}{l} Area of trapezium \\ = \frac{1}{2} \times Sum of the two \\ parallel sides \times Height \end{array} \\ = \frac{1}{2} (4 + 6) \times 8 = 40 m \end{array}

6.1 Quantity Represented by the Gradient of a Graph (Part 2)

Posted on April 24, 2020 by user

(B) Speed – Time Graph

1. The gradient of a speed-time graph is the rate of change of speed or acceleration.

(a) From O to P: Gradient = positive → (Speed of object increasing or accelerating).

(b) From P to Q: Gradient = 0 → (Object is moving at uniform speed).

(c) From Q to R: Gradient = negative → (Speed of object decreasing or decelerating).

Example:

The diagram above shows the speed-time graph of a moving car for 5 seconds. Find

(a) the rate of speed change when the car travel from X to Y.

(b) the rate of speed change when the car travel from Y to Z.

Solution:

(a)

Rate of speed change when the car travels from X to Y

= Gradient

\begin{array}{l} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ = \frac{5 - 20}{4 - 0} \\ = - \frac{15}{4} {ms}^{- 2} \leftarrow \begin{array}{l} Negative gradient indicates \\ that the speed is decreasing . \end{array} \end{array}

(b)

Rate of speed change when the car travels from Y to Z

= Gradient

\begin{array}{l} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ = \frac{10 - 5}{5 - 4} \\ = 5 {ms}^{- 2} \end{array}

6.3 SPM Practice (Long Questions)

Posted on April 24, 2020 by user

Question 1:

The diagram above shows the distance-time graph of a moving particle for 5 seconds. Find

(a) the distance travel by the particle from the time 2 second to 5 second.

(b) the speed of the particle for the first 2 seconds.

Solution:
(a)

Distance travel by the particle from the time 2 second to 5 second

= 20 – 15

= 5 m

(b)

The speed of the particle for the first 2 seconds

= Gradient

\begin{array}{l} = \frac{15 - 0}{2 - 0} \\ = 7.5 {ms}^{- 1} \end{array}

Question 2:

The diagram above shows the distance-time graph of a moving car for 12 seconds. Find

(a) the value of v, if the average speed of the car for the first 6 seconds is 2 ms^-1.

(b) average speed of the car for the first 8 seconds.

Solution:
(a)

\begin{array}{l} {Average speed of the car for the first 6 seconds is 2 ms}^{-1} \\ \frac{Total distance travelled}{Total time taken} = 2 \\ \frac{v}{6} = 2 \\ v = 12 \end{array}

(b)

\begin{array}{l} Average speed of the car for the first 8 seconds \\ = \frac{15}{8} \\ = 1.875 m s^{- 1} \end{array}

6.3 SPM Practice (Long Questions)

Posted on April 24, 2020 by user

Question 3:
Diagram below shows the distance-time graph for the journey of a train from one town to another for a period of 90 minutes.

(a) State the duration of time, in minutes, during which the train is stationery.
(b) Calculate the speed, in km h^-1, of the train in the first 40 minutes.
(c) Find the distance, in km, travelled by the train for the last 25 minutes.

Solution:
(a) Duration the train is stationery = 65 – 40 = 25 minutes

\begin{array}{l} (b) \\ Speed of the train in the first 40 minutes \\ = \frac{150 - 90 km}{40 minutes} \\ = \frac{60 km}{\frac{40}{60} h} \\ = 90 km / h \end{array}

Question 4:

The diagram above shows the speed-time graph of a moving particle for 10 seconds. From the graph above, find

(a) the total distance travel by the particle for the whole journey.

(b) the average speed for the whole journey.

Solution:
(a)

Total distance travelled

= Area under the speed-time graph

= Area of triangle

= ½ × 15 × 10

= 75 m

(b)
Average speed for the whole journey

\begin{array}{l} = \frac{Total distance travelled}{Total time taken} \\ = \frac{75}{10} \\ = 7.5 m s^{- 1} \end{array}

6.3 SPM Practice (Long Questions)

Posted on April 24, 2020 by user

Question 5:

The diagram above shows the speed-time graph of a moving particle for 12 seconds. Find

(a) the length of the time, in s that the particle move with uniform speed.

(b) the distance travel by the particle when it move with constant speed.

(c) the distance travel by the particle when the rate of the speed change is negative.

Solution:
(a)

Length of the time the particle move with uniform speed

= 10 – 6

= 4 s

(b)

Distance travel by the particle when it move with constant speed

= Area under the speed-time graph

= Area of rectangle

= 4 × 10

= 40 m

(c)

Distance travel by the particle when the rate of the speed change is negative

= Area under the speed-time graph for the first 6 s

= Area of trapezium

= ½ (10 + 25)(6)

= 105 m

Question 6:
Diagram below shows the speed-time graph for the movement of an object for a period of 40 seconds.

(a) State the duration of time, in s, for which the object moves with uniform speed.
(b) Calculate the rate of change of speed, in ms^-2, of the object for the last 12 seconds.
(c) Calculate the value of v, if the total distance travelled for the period of 40 seconds is 500 m.

Solution:
(a) Duration of time the object moves with uniform speed = 28s – 10s = 18s

\begin{array}{l} (b) \\ Rate of change of speed \\ = - \frac{15}{12} {ms}^{- 2} \\ = - 1.25 {ms}^{- 2} \\ (c) \\ Area of trapezium I + Area of trapezium II = 500 \\ \frac{1}{2} (v + 15) 10 + \frac{1}{2} (18 + 30) 15 = 500 \\ 5 v + 75 + 360 = 500 \\ 5 v = 65 \\ v = 13 \end{array}