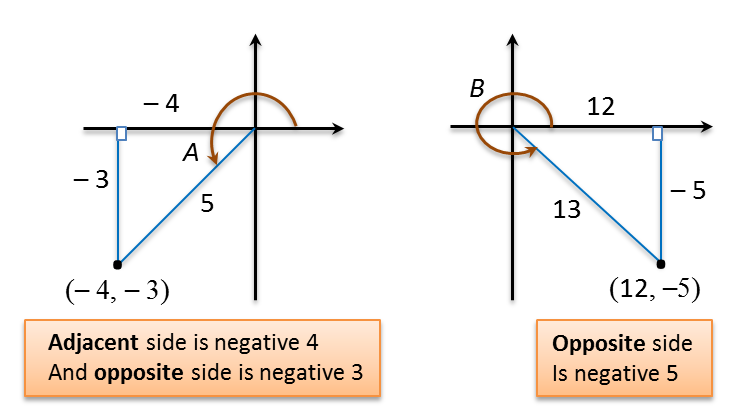
Example 5
Given that and , evaluate the following.
(a)
(b)
(c)
(d)
Solution:
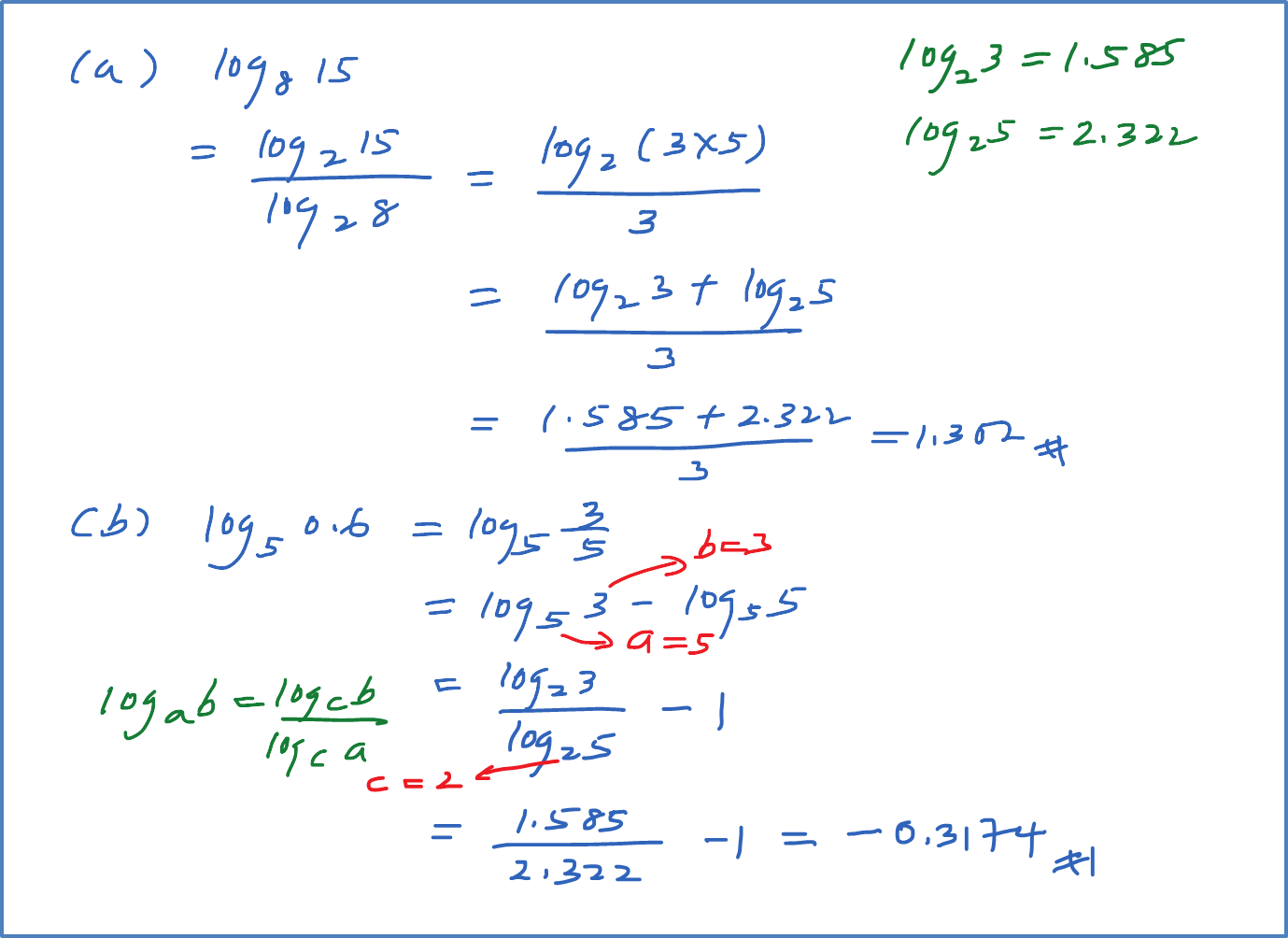
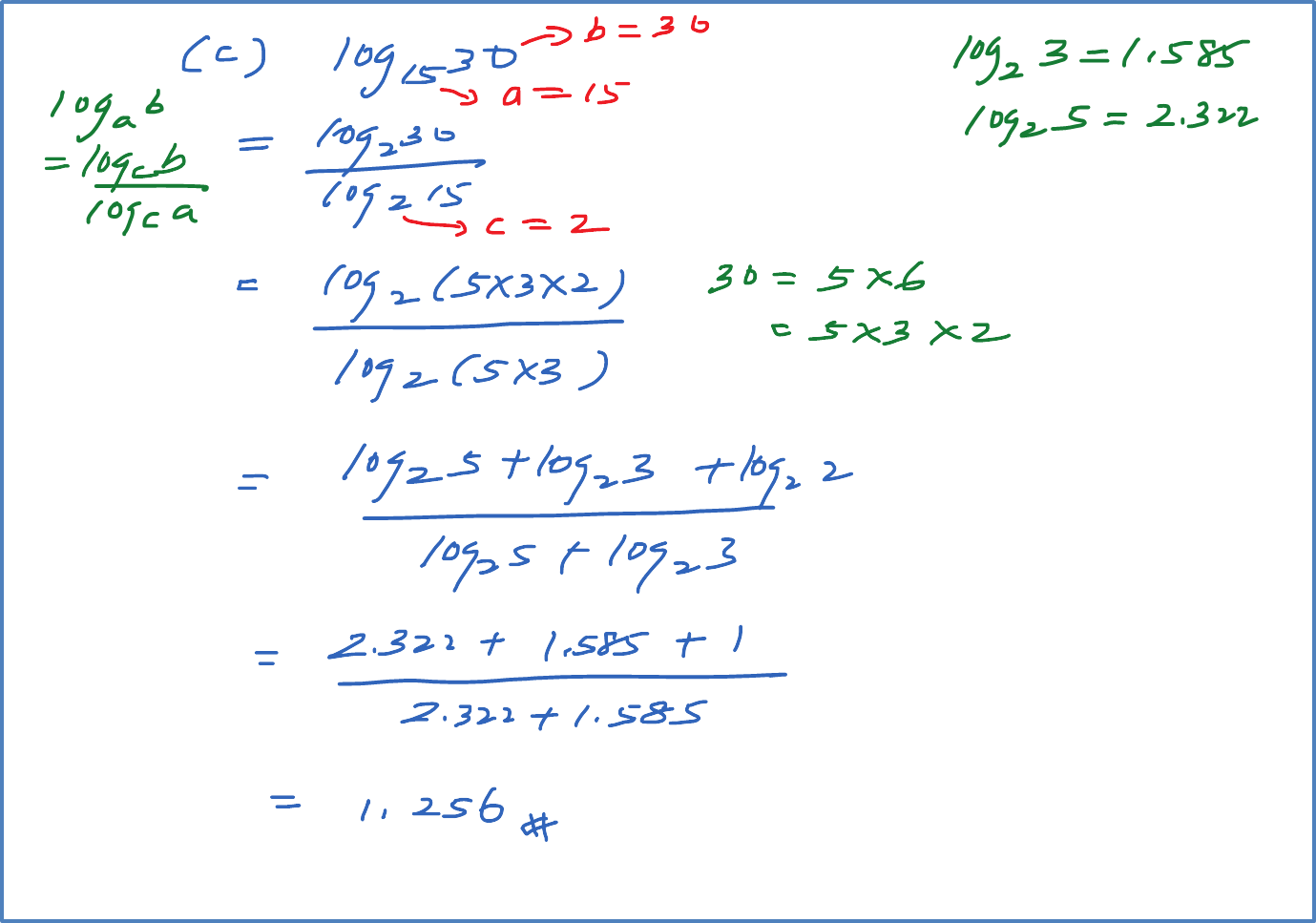
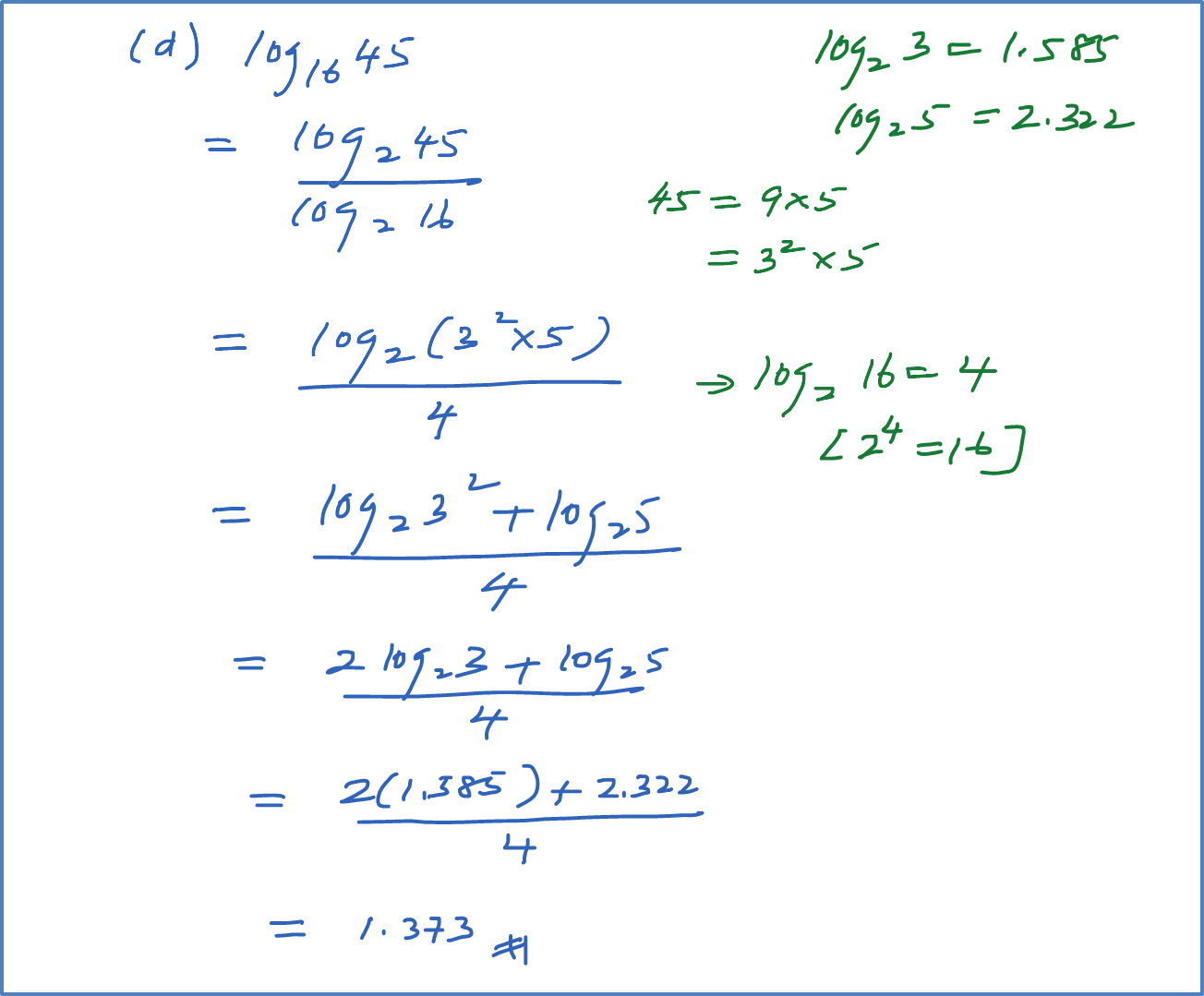
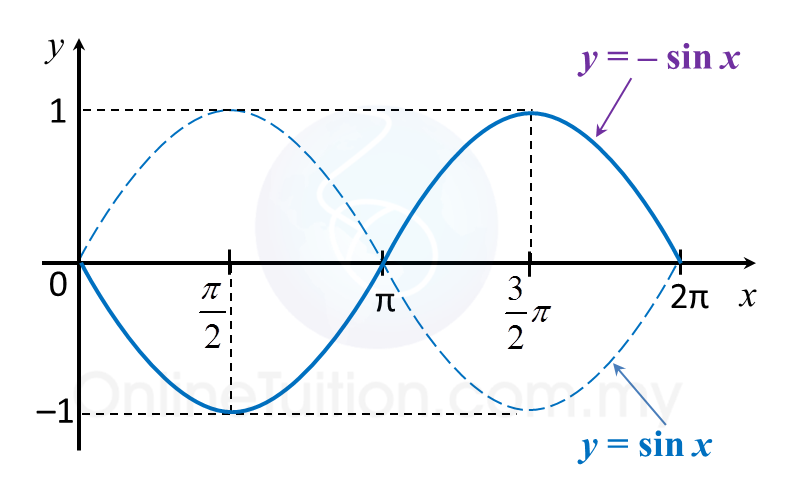
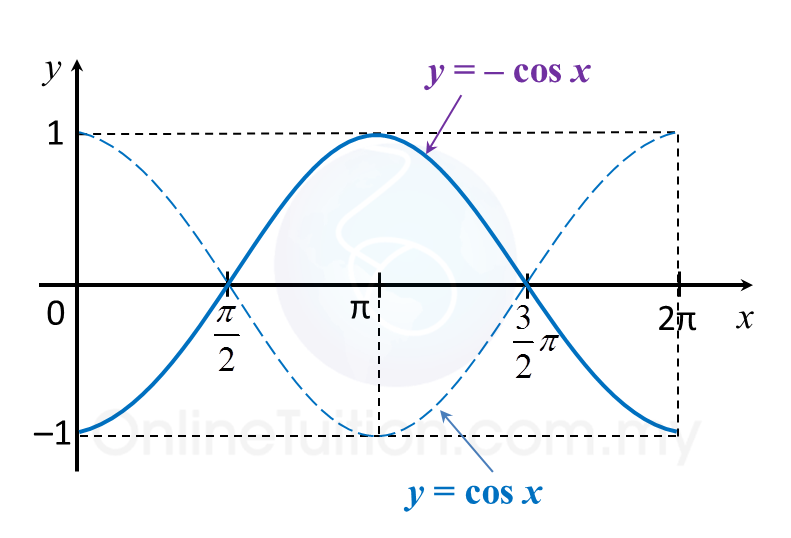
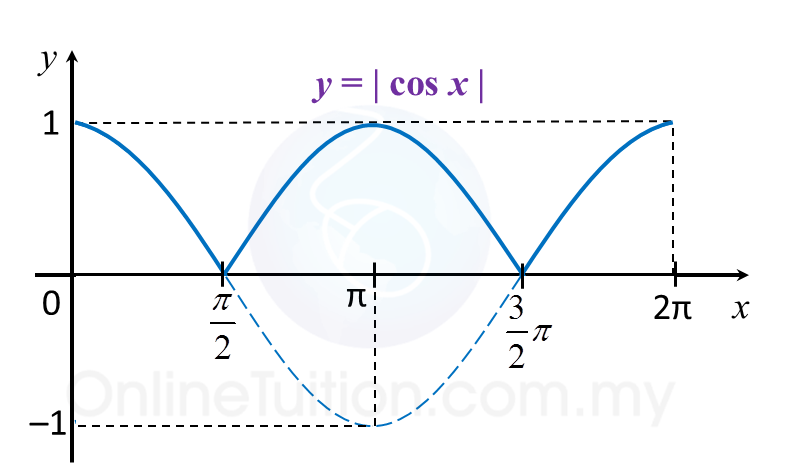
Given that and , evaluate the following.
(a)
(b)
(c)
(d)
Solution:
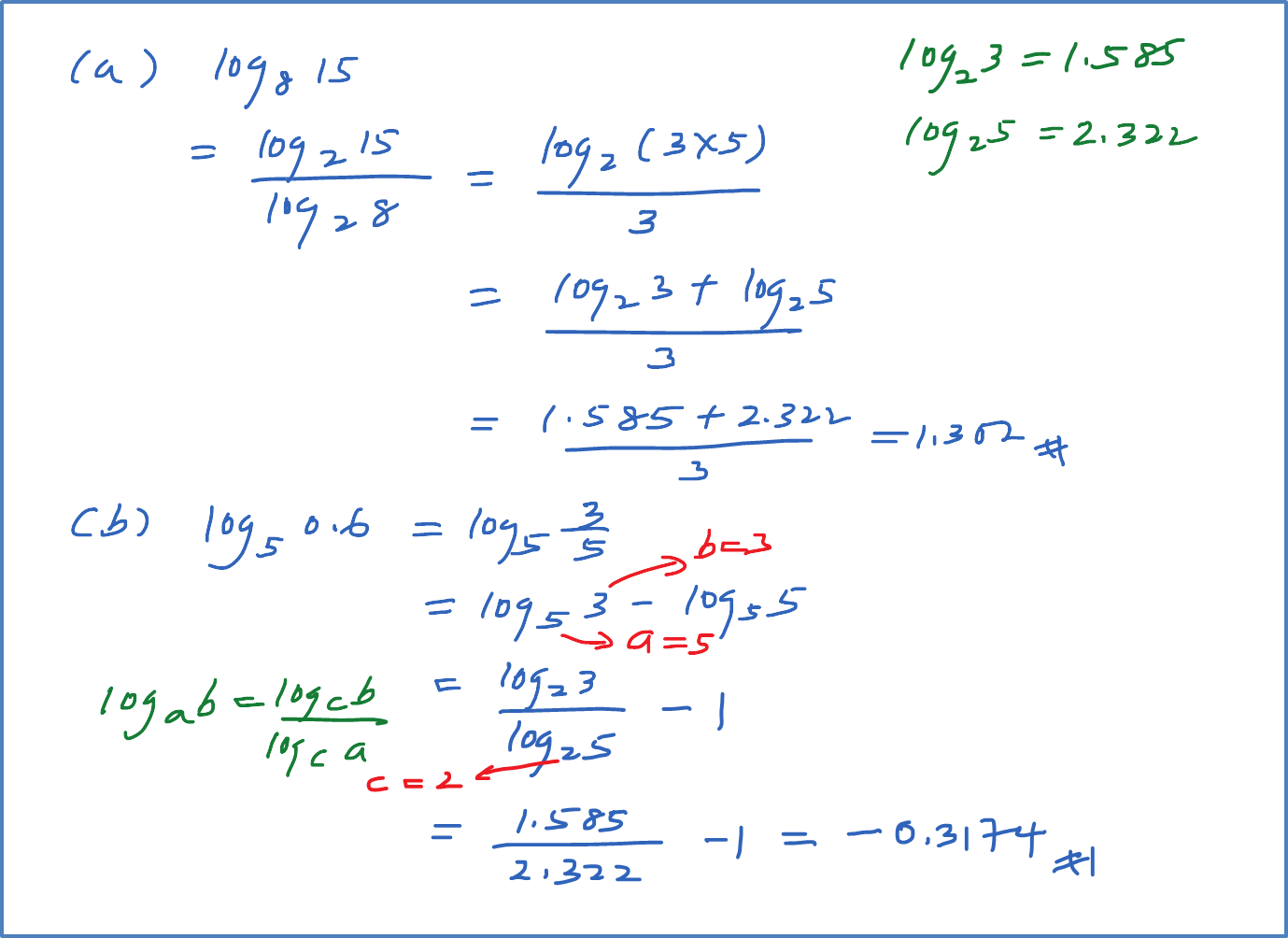
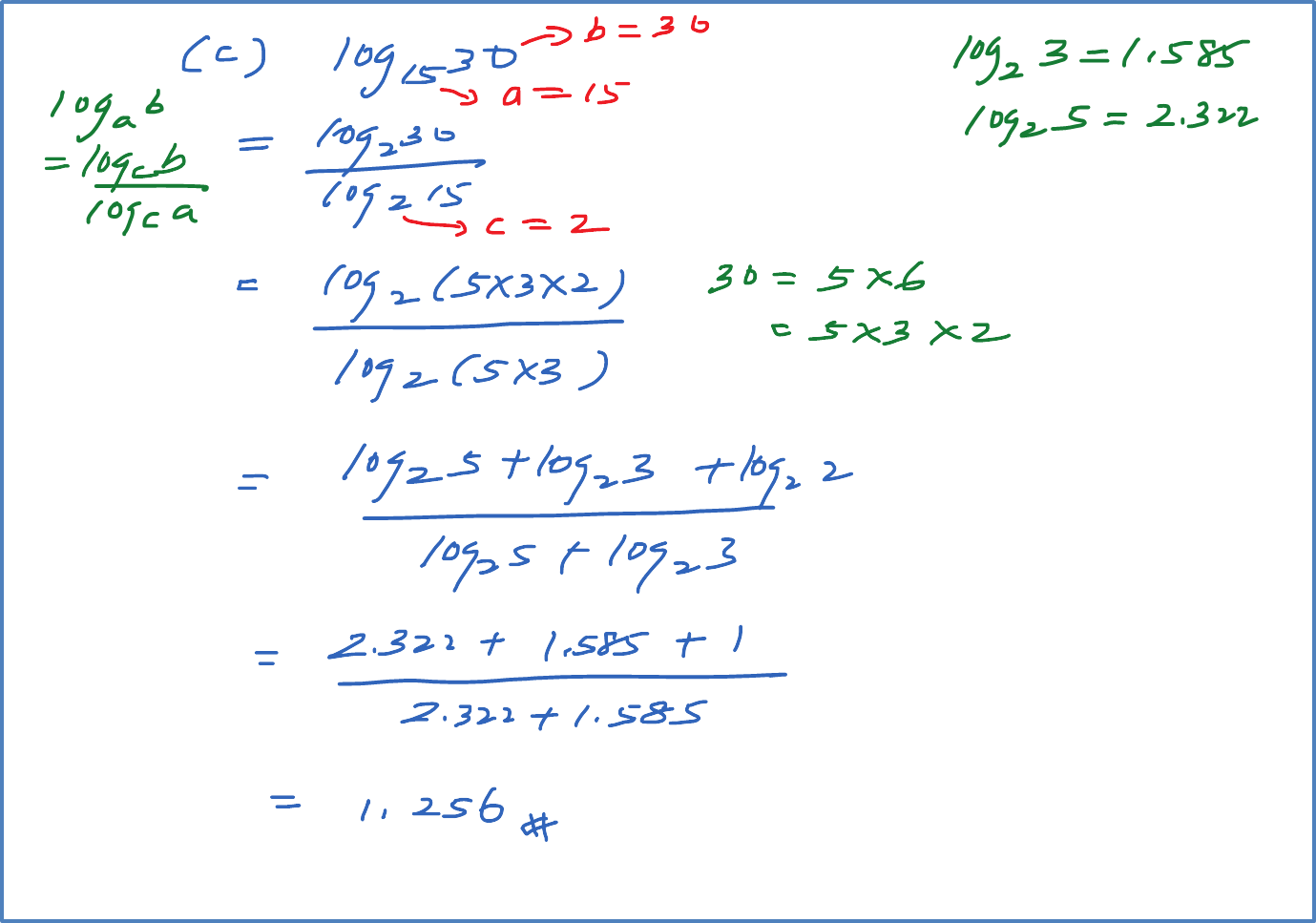
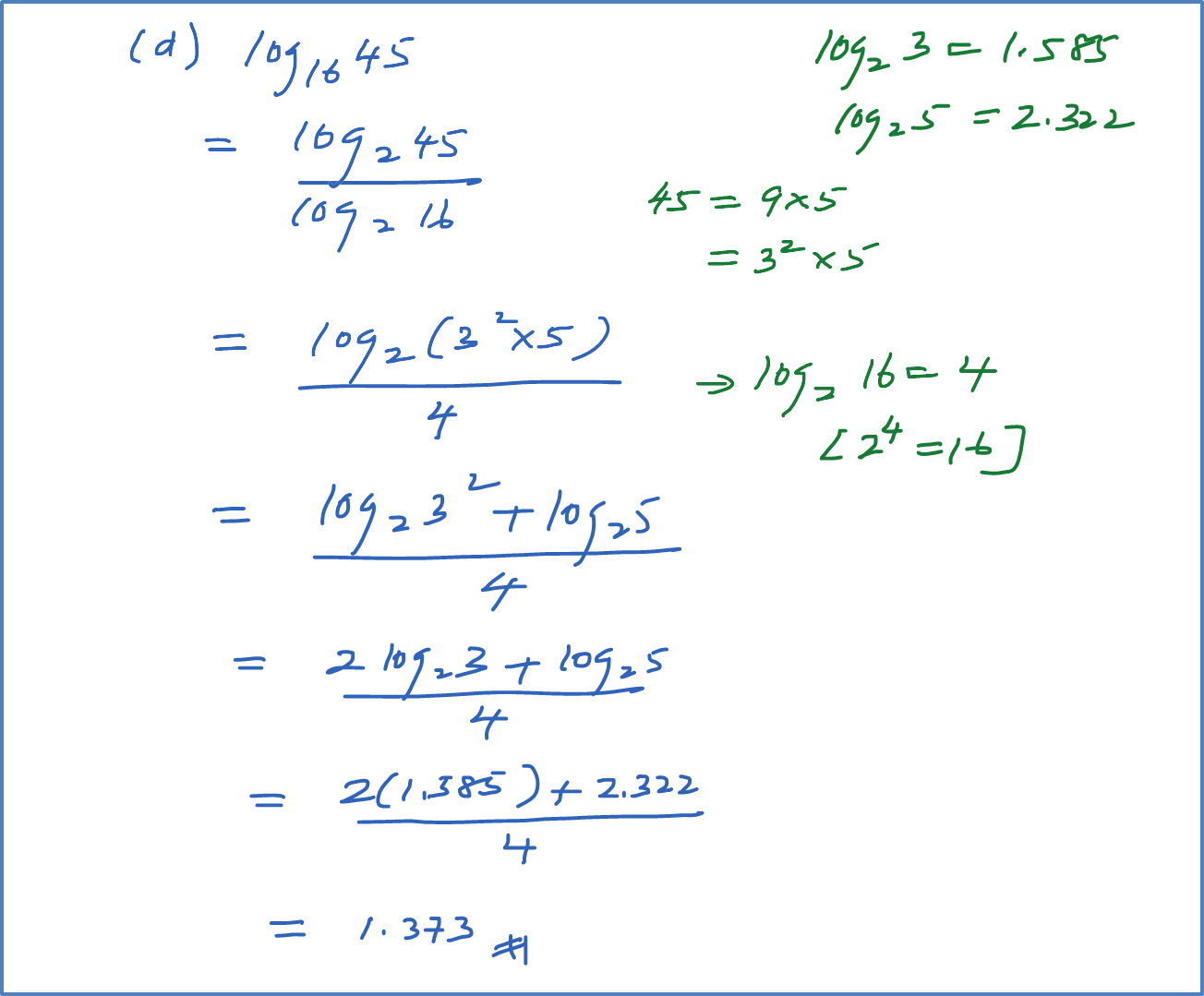
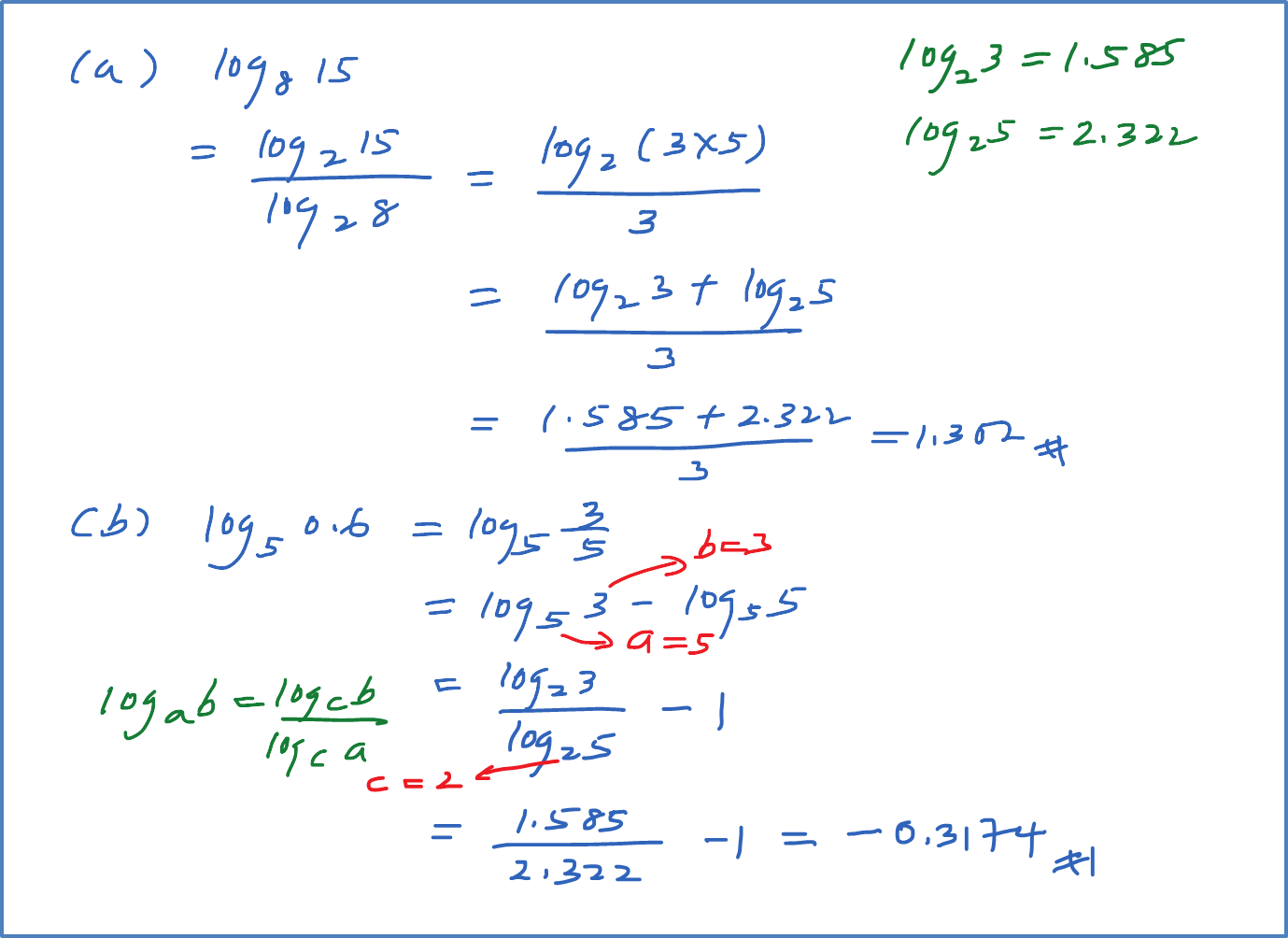
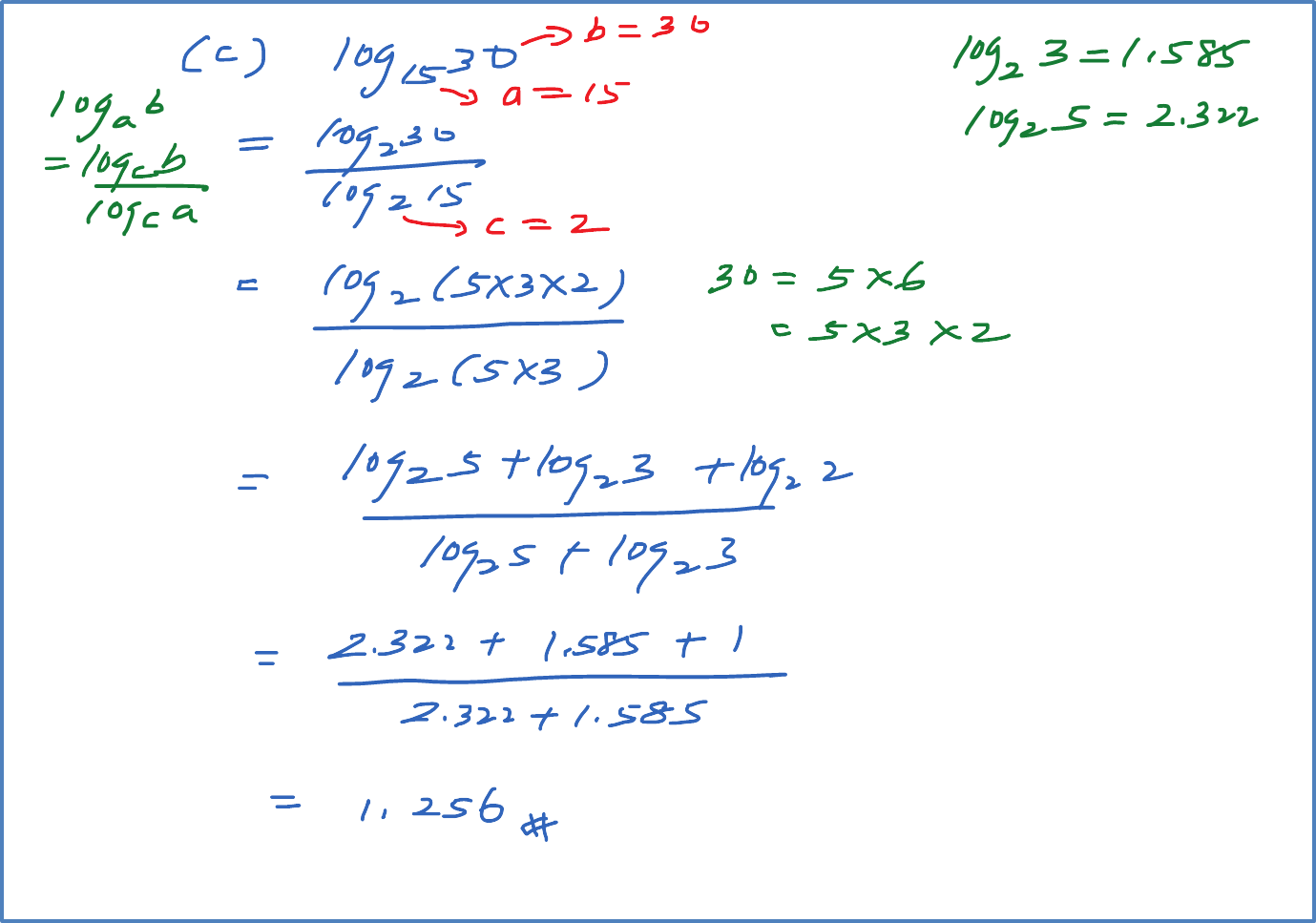
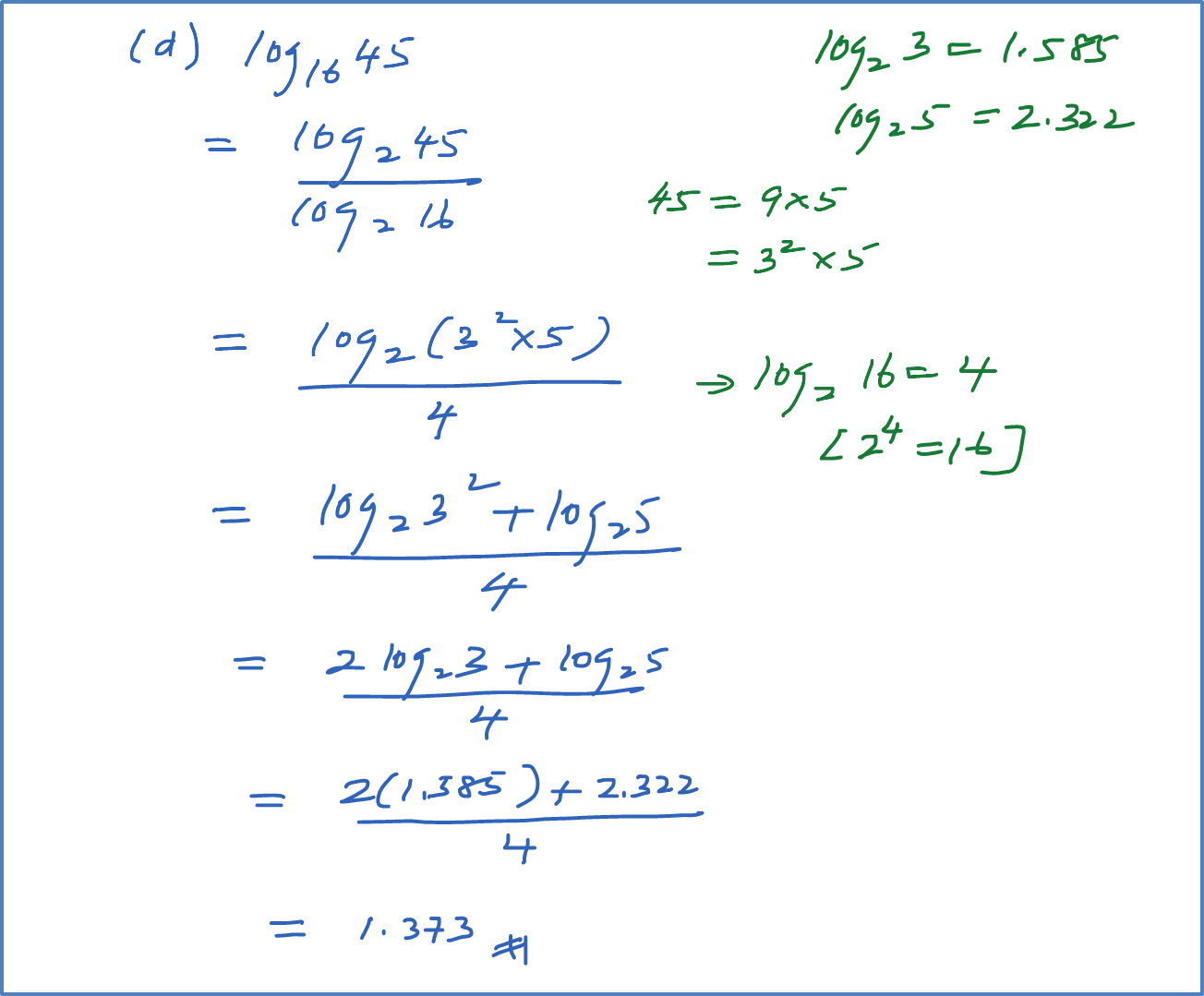

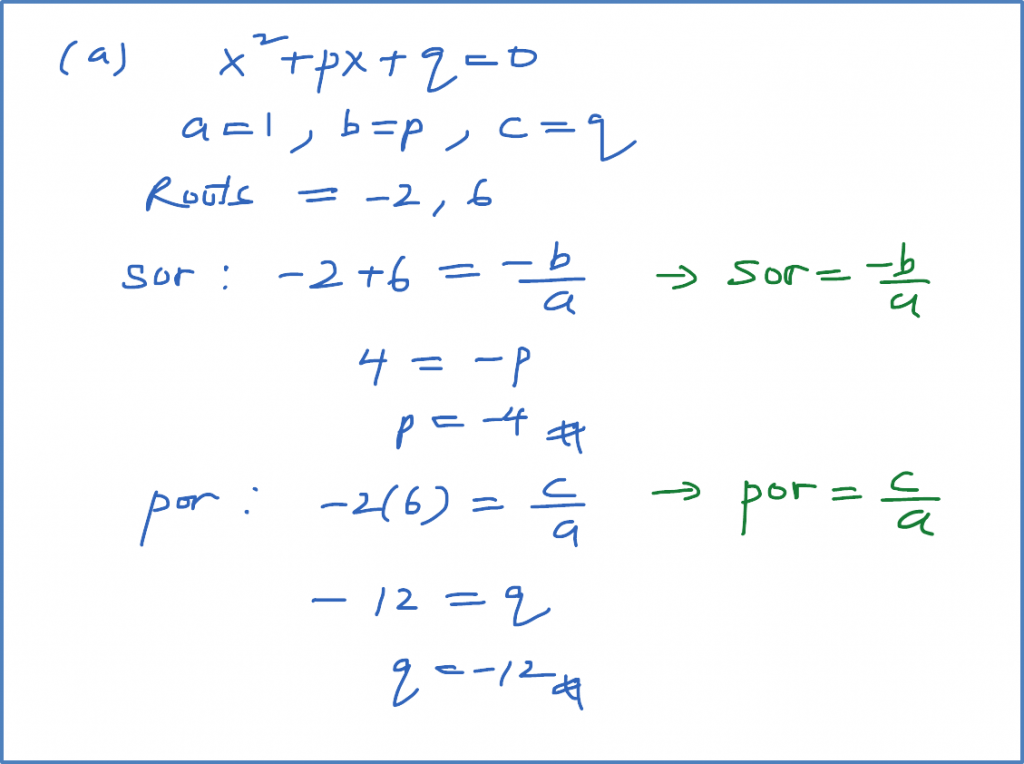





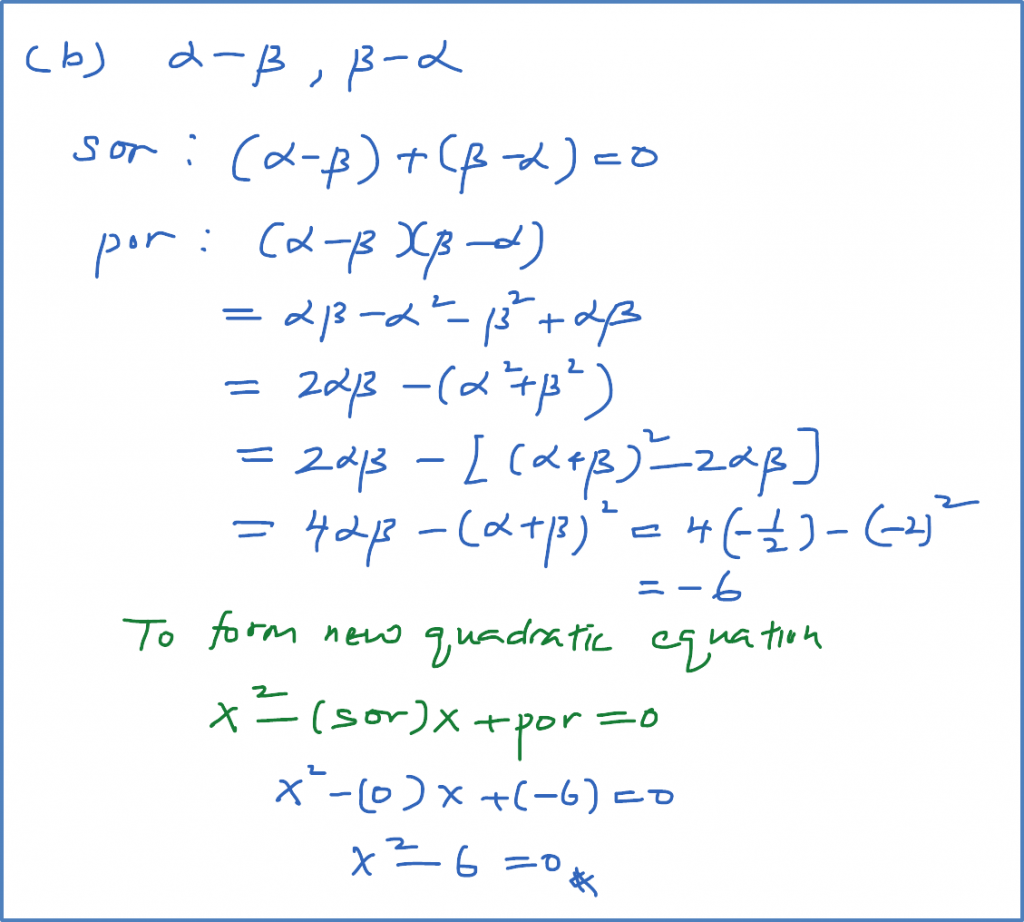


Z |
6 |
5 (Subtract) |
1.6 |
.0485 |
5 |
Z |
7 |
4 (Subtract) |
0.9 |
.1660 |
10 |