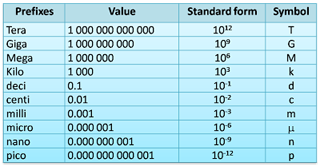
Prefixes are the preceding factor used to represent very small and very large physical quantities in SI units.
Table below shows the prefixes that you need to know in SPM.
Conversion of prefixes
Prefixes to Normal Number
Example 1:
The frequency of the radio wave is 350M Hz. What is the frequency of the radio wave in Hz?
Answer:
Mega (M) = 1,000,000 or 106
Therefore,
350MHz = 350 x 106Hz
The frequency of the radio wave is 350M Hz. What is the frequency of the radio wave in Hz?
Answer:
Mega (M) = 1,000,000 or 106
Therefore,
350MHz = 350 x 106Hz
Example 2:
The thickness of a film is 25nm. What is the thickness in unit meter?
Answer:
nano (n) = 0.000000001 or 10-9
Therefore
25nm = 25 x 10-9m
The thickness of a film is 25nm. What is the thickness in unit meter?
Answer:
nano (n) = 0.000000001 or 10-9
Therefore
25nm = 25 x 10-9m
Normal number to Prefixes
Example 3:
0.255 s is equal to how many ms.
Answer:
mili (m) = 0.001 or 10-3
To write a normal number with prefixes, we divide the number with the value of the prefixes
0.0255 s = 0.0255 ÷ 10-3 = 25.5 ms
0.255 s is equal to how many ms.
Answer:
mili (m) = 0.001 or 10-3
To write a normal number with prefixes, we divide the number with the value of the prefixes
0.0255 s = 0.0255 ÷ 10-3 = 25.5 ms
Example 4:
Convert 265,500,000 W into GW.
Answer:
Gega (G) = 1,000,000,000 or 109
Therefore
265,500,000 W = 265,500,000 ÷ 109 = 0.2655GW
Convert 265,500,000 W into GW.
Answer:
Gega (G) = 1,000,000,000 or 109
Therefore
265,500,000 W = 265,500,000 ÷ 109 = 0.2655GW

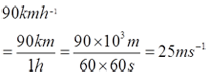
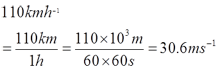



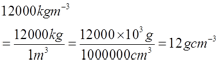
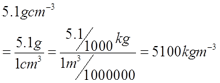
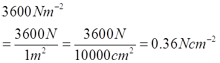
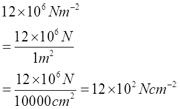
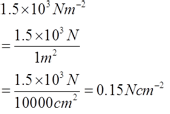
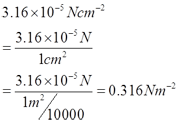


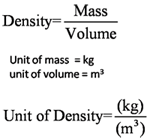















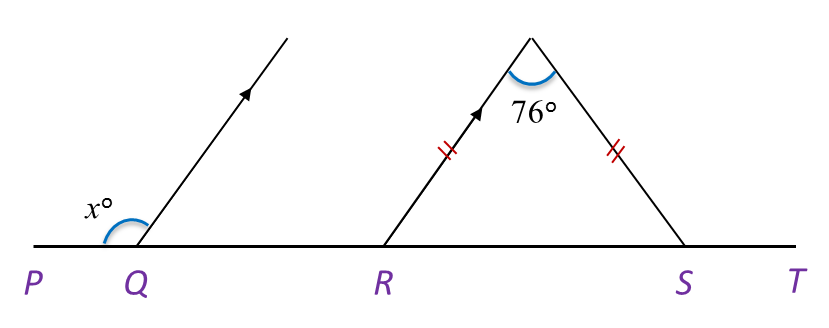

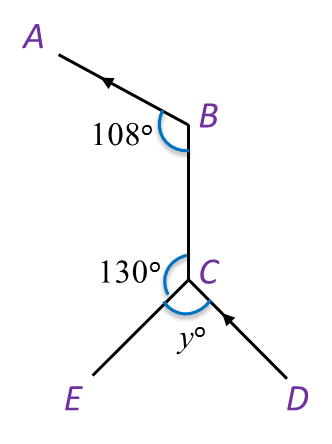
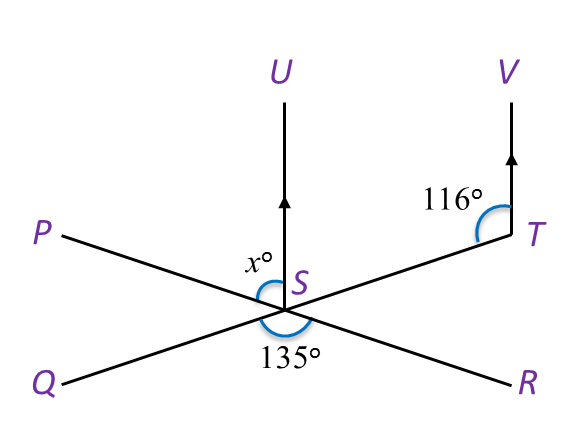 Find the value of x.
Find the value of x. (a) Which line is perpendicular to line PWV?
(a) Which line is perpendicular to line PWV?


 h2 = 32 + 42
h2 = 32 + 42