10.2.1 Circles I, PT3 Focus Practice

Posted on October 5, 2017 by user

10.2.1 Circles I, PT3 Focus Practice

Question 1:

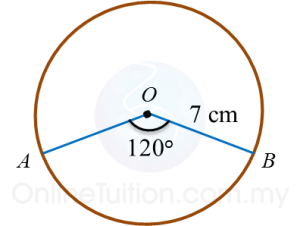
Diagram below shows a circle with centre O.

The radius of the circle is 35 cm.

Calculate the length, in cm, of the major arc AB.

(Use π = \frac{22}{7})

Solution:

Angle of the major arc AB = 360^o – 144^o= 216^o

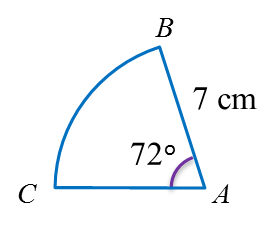
\begin{array}{l} Length of major arc A B \\ = \frac{216^{o}}{360^{o}} \times 2 π r \\ = \frac{216^{o}}{360^{o}} \times 2 \times \frac{22}{7} \times 35 \\ = 132 cm \end{array}

Question 2:

In diagram below, O is the centre of the circle. SPQ and POQ are straight lines.

The length of PO is 8 cm and the length of POQ is 18 cm.

Calculate the length, in cm, of SPT.

Solution:

Radius = 18 – 8 = 10 cm

PT²= 10² – 8²

= 100 – 64

= 36

PT = 6 cm

Length of SPT = 6 + 6

= 12 cm

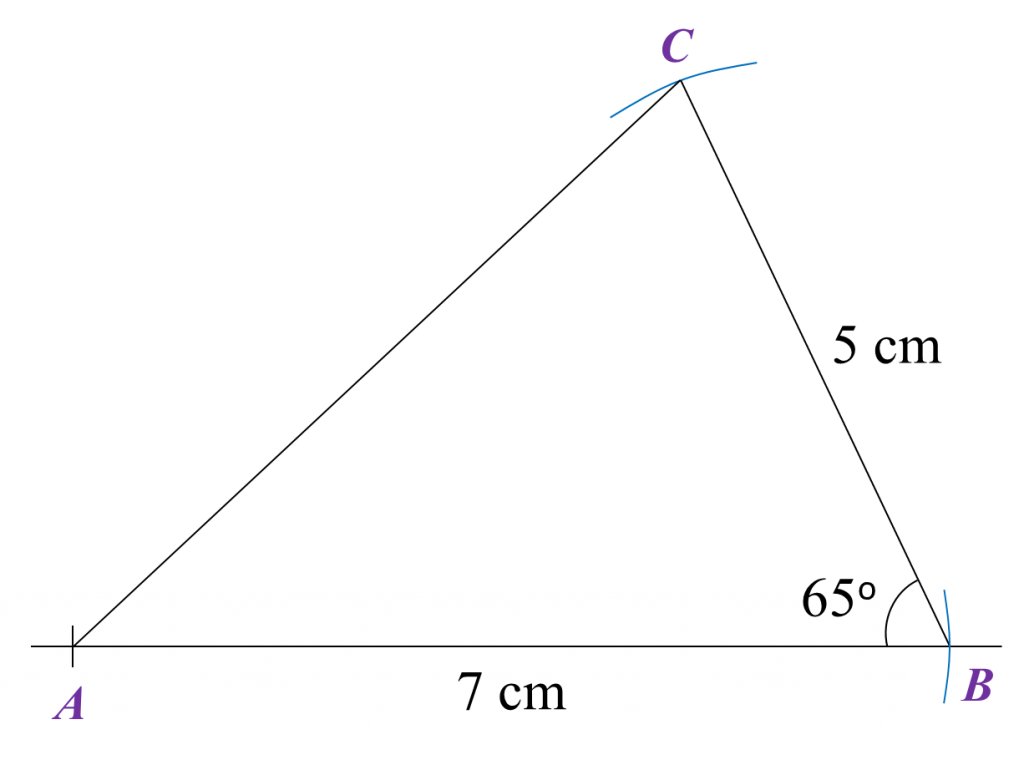
Question 3:

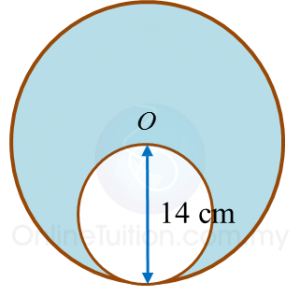
Diagram below shows two circles. The bigger circle has a radius of 14 cm with its centre at O.

The smaller circle passes through O and touches the bigger circle.

Calculate the area of the shaded region.

(Use π = \frac{22}{7})

Solution:

\begin{array}{l} Area of bigger circle = π R^{2} = \frac{22}{7} \times 14^{2} \\ Radius, r of smaller circle = \frac{1}{2} \times 14 = 7 cm \\ Area of smaller circle = π r^{2} = \frac{22}{7} \times 7^{2} \\ ∴ Area of shaded region \\ = (\frac{22}{7} \times 14^{2}) - (\frac{22}{7} \times 7^{2}) \\ = 616 - 154 \\ = 462 {cm}^{2} \end{array}

Question 4:

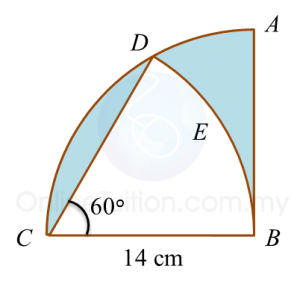
Diagram below shows two sectors. ABCD is a quadrant and BED is an arc of a circle with centre C.

Calculate the area of the shaded region, in cm².

(Use π = \frac{22}{7})

Solution:

\begin{array}{l} The area of sector C B E D \\ = \frac{60^{o}}{360^{o}} \times π r^{2} \\ = \frac{60^{o}}{360^{o}} \times \frac{22}{7} \times 14^{2} \\ = 102 \frac{2}{3} {cm}^{2} \end{array}

\begin{array}{l} The area of quadrant A B C D \\ = \frac{1}{4} \times π r^{2} \\ = \frac{1}{4} \times \frac{22}{7} \times 14^{2} \\ = 154 {cm}^{2} \end{array}

\begin{array}{l} Area of the shaded region \\ = 154 - 102 \frac{2}{3} \\ = 51 \frac{1}{3} {cm}^{2} \end{array}

Question 5:

Diagram below shows a square KLMN. KPN is a semicircle with centre O.

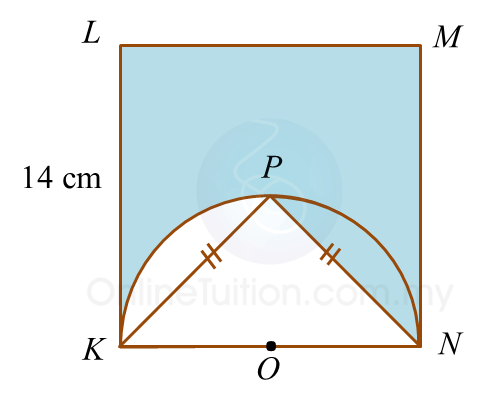
Calculate the perimeter, in cm, of the shaded region.

(Use π = \frac{22}{7})

Solution:

\begin{array}{l} K O = O N = O P = 7 cm \\ P N = \sqrt{7^{2} + 7^{2}} \\ = \sqrt{98} \\ = 9.90 cm \\ Arc length K P \\ = \frac{1}{4} \times 2 \times \frac{22}{7} \times 7 \\ = 11 cm \end{array}

Perimeter of the shaded region

= KL + LM + MN + NP + Arc length PK

= 14 + 14 +14 + 9.90 + 11

= 62.90 cm

10.1 Circles I

Posted on October 1, 2017 by user

10.1 Circles I

10.1.1 Parts of a Circle

1. A circle is set of points in a plane equidistant from a fixed point.

2. Parts of a circle:

(a) The centre, O, of a circle is a fixed point which is equidistant from all points on the circle.

(b) A sector is the region enclosed by two radii and an arc.

(c) An arc is a part of the circumference of a circle.

(d) A segment is an area enclosed by an arc and a chord.

10.1.2 Circumference of a Circle

\begin{array}{l} circumference = π d, where d = d i a m e t e r \\ = 2 π r, where r = r a d i u s \\ π (p i) = \frac{22}{7} or 3.142 \end{array}

Example:

Calculate the circumference of a circle with a diameter of 14 cm.

(π = \frac{22}{7})

Solution:

\begin{array}{l} Circumference = π \times Diameter \\ = \frac{22}{7} \times 14 \\ = 44 cm \end{array}

10.1.3 Arc of a Circle

The length of an arc of a circle is proportional to the angle at the centre.

\begin{array}{l} \frac{Length of arc}{Circumference} = \frac{Angle at centre}{360^{o}} \end{array}

Example:

Calculate the length of the minor arc AB of the circle above.

(π = \frac{22}{7})

Solution:

\begin{array}{l} \frac{Length of arc}{Circumference} = \frac{Angle at centre}{360^{o}} \\ Length of arc A B = \frac{120^{o}}{360^{o}} \times 2 \times \frac{22}{7} \times 7 \\ = 14 \frac{2}{3} cm \end{array}

10.1.4 Area of a Circle

\begin{array}{l} Area of a circle = π \times {(radius)}^{2} \\ = π r^{2} \end{array}

Example:

Calculate the area of each of the following circles that has

(a) a radius of 7 cm,

(b) a diameter of 10 cm.

(π = \frac{22}{7})

Solution:

(a)

\begin{array}{l} Area of a circle = π r^{2} \\ = \frac{22}{7} \times 7 \times 7 \\ = 154 {cm}^{2} \end{array}

(b)

\begin{array}{l} Diameter of circle = 10 cm \\ Radius of circle = 5 cm \\ Area of circle = π r^{2} \\ = \frac{22}{7} \times 5 \times 5 \\ = 78.57 {cm}^{2} \end{array}

10.1.5 Area of a Sector

The area of a sector of a circle is proportional to the angle at the centre.

\begin{array}{l} \frac{Area of sector}{Area of circle} = \frac{Angle at centre}{360^{o}} \end{array}

Example:

\begin{array}{l} Area of sector A B C \\ = \frac{72^{o}}{360^{o}} \times \frac{22}{7} \times 7 \times 7 \\ = 30 \frac{4}{5} {cm}^{2} \end{array}

9.2.3 Loci in Two Dimensions, PT3 Focus Practice

Posted on September 24, 2017 by user

Question 7:
Diagram below in the answer space shows a circle with centre O drawn on a grid of equal squares with sides of 1 unit. POQ is a diameter of the circle.
W, X and Y are three moving points inside the circle.
(a) W is the point which moves such that it is constantly 4 units from the point O. Describe fully the locus of W.
(b) On the diagram, draw,
(i) the locus of the point X which moves such that its distance is constantly 3 units from the line PQ,
(ii) the locus of the point Y which moves such that it is equidistant from the point P and the point Q.
(c) Hence, mark with the symbol

\otimes

the intersection of the locus of X and the locus of Y.

Answer:
(b)(i),(ii) and (c)

Solution:
(a) The locus of W is a circle with the centre O and a radius of 4 units.

(b)(i),(ii) and (c)

Question 8:
The diagram in the answer space shows two squares ABCD and CDEF each of sides 4 cm. K is a point on the line CD. W, X and Y are three moving points in the diagram.
(a) Point W moves such that it is always equidistant from the straight lines AB and EF. By using the letters in diagram, state the locus of W.
(b) On the diagram, draw
(i) the locus X such that it is always 2 cm from the straight line ACE,
(ii) the locus of Y such that KY = KC.
(c) Hence, mark with the symbol

\otimes

the intersection of the locus of X and the locus of Y.

Answer:
(b)(i), (ii) and (c)

Solution:
(a) The locus of W is the line CD.

(b)(i),(ii) and (c)

Question 9:
Diagram below shows a Cartesian plane.
Draw the locus of X, Y and Z.
(a) X is a point which moves such that its distance is constantly 4 units from the origin.
(b) Y is a point which moves such that it is always equidistant from point K and point L.
(c) Z is a point which moves such that it is always equidistant from lines KM and y-axis.

Answer:

Solution:

9.2.2 Loci in Two Dimensions, PT3 Focus Practice

Posted on September 21, 2017 by user

9.2.2 Loci in Two Dimensions, PT3 Focus Practice

Question 4:

Diagram below in the answer space shows a quadrilateral ABCD drawn on a grid of equal squares with sides of 1 unit.

X, Y and Z are three moving points inside the quadrilateral ABCD.

(a) X is the point which moves such that it is always equidistant from point B and point D.

By using the letters in diagram, state the locus of X.

(b) On the diagram, draw,
(i) the locus of the point Y such that it is always 6 units from point A,
(ii) the locus of the point Z which moves such that its distance is constantly 3 units from the
line AB.

Answer:

(b)(i),(ii) and (c)

Solution:

(a) The locus of X is the line AC.

(b)(i),(ii) and (c)

Question 5:

Diagram in the answer space below shows a square ABCD. E, F, G and H are the midpoints of straight lines AD, AB, BC and CD respectively. W, X and Y are moving points in the square.

On the diagram,

(a) draw the locus of the point W which moves such that it is always equidistant from point AD and BC.

(b) draw the locus of the point X which moves such that XM = MG.

(d) Hence, mark with the symbol ⊗ the intersection of the locus of W and the locus of Y.

Answer:

(a), (b), (c) and (d)

Solution:

Question 6:
Diagram in the answer space below shows a polygon ABCDEF drawn on a grid of squares with sides of 1 unit. X, Y and Z are the points that move in the polygon.
(a) X is a point which moves such that it is equidistant from point B and point F.
By using the letters in diagram, state the locus of X.
(b) On the diagram, draw
(i) the locus of the point Y which moves such that it is always parallel and equidistant from the straight lines BA and CD.
(ii) the locus of point Z which moves such that its distance is constantly 6 units from the point A.
(c) Hence, mark with the symbol

\otimes

the intersection of the locus of Y and the locus of Z.

Answer:
(b)(i), (ii) and (c)

Solution:

(a) The locus of X is AD.

(b)(i),(ii) and (c)

9.2.1 Loci in Two Dimensions, PT3 Focus Practice

Posted on September 18, 2017 by user

9.2.1 Loci in Two Dimensions, PT3 Focus Practice

Question 1:

Diagram below in the answer space shows a square PQRS with sides of 6 units drawn on a grid of equal squares with sides of 1 unit. W, X and Y are three moving points inside the square.

(a) W is the point which moves such that it is always equidistant from point P and point R.

By using the letters in diagram, state the locus of W.

(b) On the diagram, draw,

(i) the locus of the point X which moves such that it is always equidistant from the straight lines PQ and PS,

(ii) the locus of the point Y which moves such that its distance is constantly 2 units from point K.

Answer:

(b)(i),(ii)

Solution:

(a) QS

(b)(i),(ii)

(c)

Question 2:

Diagram in the answer space below, shows a regular pentagon PQRST. W, X and Y are moving points which move in the pentagon.

On the diagram,

(a) draw the locus of the point W which moves such that it is always equidistant from point R and S.

(b) draw the locus of the point X which moves such that XR = RS.

(d) hence, mark with the symbol ⊗ the intersection of the locus of W and the locus of X.

Answer:

(a), (b), (c) and (d)

Solution:

(a), (b), (c) and (d)

Question 3:
Diagram in the answer space below shows a polygon. X and Y are two moving points in the polygon.
(a) On the diagram, draw
(i) the locus of the point X such that XQ = XR.
(ii) the locus of the point Y such that YQ = QR.
(b) Hence, mark with the symbol

\otimes

the intersection of the locus of X and the locus of Y.

Answer:

(a)(i), (ii) and (b)

Solution:

(a)(i), (ii) and (b)

8.2.3 Coordinates, PT3 Focus Practice

Posted on September 10, 2017 by user

Question 11:
Diagram below shows the route of a Negaraku Run.

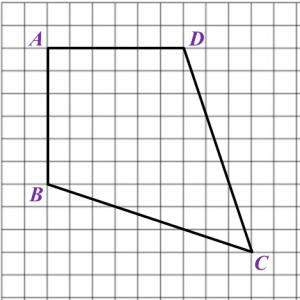
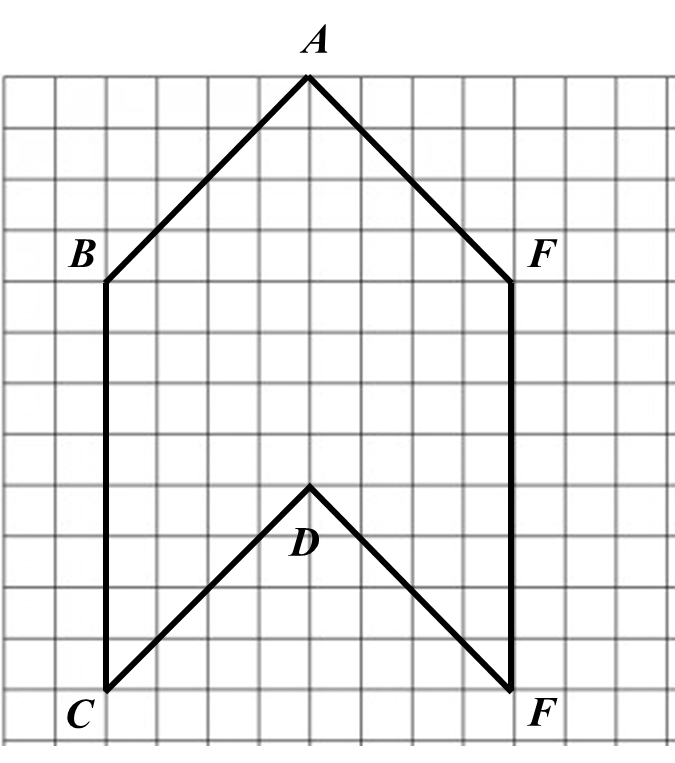
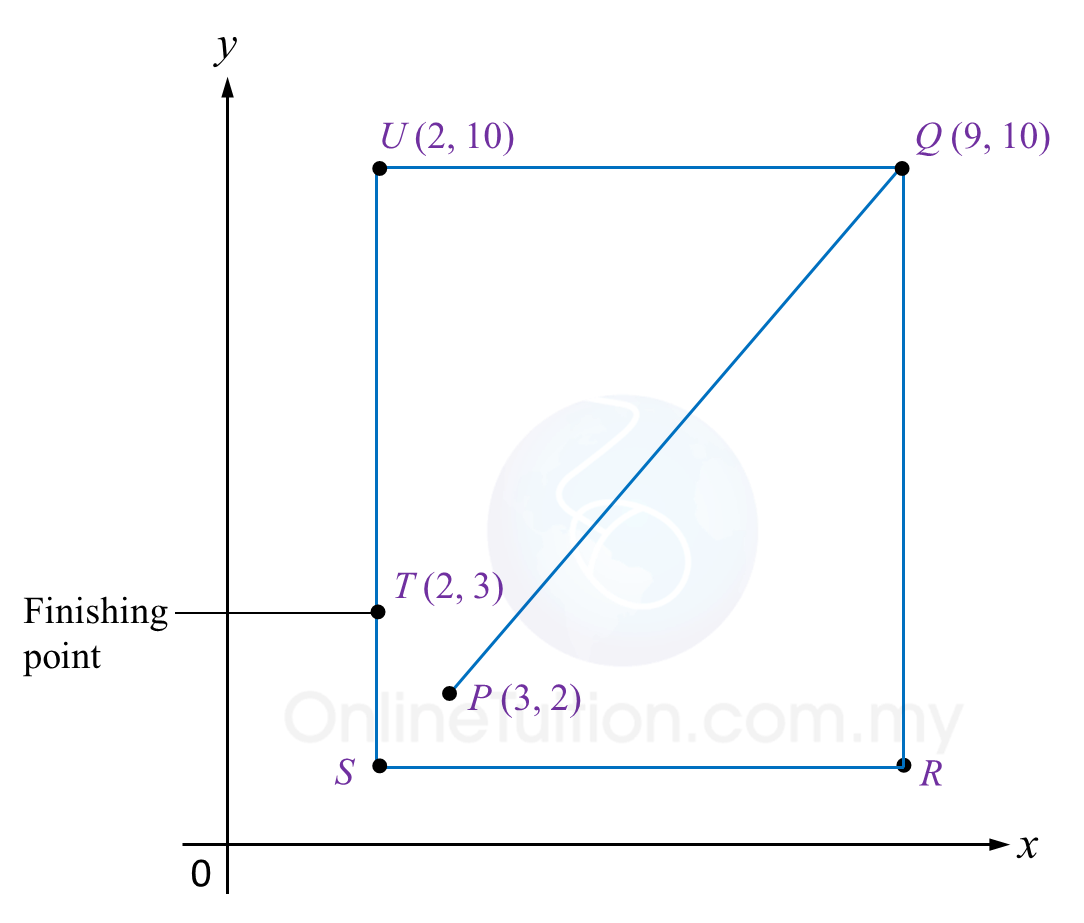The route of male participants is PQUT while the route for female participants is QRST. QR is parallel to UT whereas UQ is parallel to SR.
(a) Given the distance between point Q and point R is 9 km, state the coordinates of point R.
(b) It is given that the male participants start the run at point P and the female participants at point Q.
Find the difference of distance, in km, between the male and female participants.

Solution:
(a)
R = (9, 1)

(b)
Route of male participants
= PQ + QU + UT
= 10 + 7 + 7
= 24 km

Route of female participants
= QR + RS + ST
= 9 + 7 + 2
= 18 km

Difference in distance
= 24 – 18
= 6 km

Question 12:
Diagram below shows a parking lot in the shape of trapezium, RSTU. Two coordinates from the trapezium vertices are R(–30, –4) and S(20, –4).

(a) Given the distance between vertex S and vertex T is 22 units.
State the coordinates of vertex T.
(b) Given the area of the parking lot is 946 unit², find the coordinates of U.

Solution:
(a)
y-coordinates of T = –4 + 22 = 18
T = (20, 18)

(b)

\begin{array}{l} Area of trapezium = 946 {unit}^{2} \\ \frac{1}{2} \times (U T + R S) \times S T = 946 \\ \frac{1}{2} \times (U T + 50) \times 22 = 946 \\ U T + 50 = \frac{946 \times 2}{22} \\ U T + 50 = 86 \\ U T = 36 \\ x - coordinate of point U = 20 - 36 = - 16 \\ y - coordinate of point U = 18 \\ U = (- 16, 18) \end{array}

8.2.1 Coordinates, PT3 Focus Practice

Posted on September 5, 2017 by user

8.2.1 Coordinates, PT3 Focus Practice

Question 1:

In diagram below, Q is the midpoint of the straight line PR.

The value of m is

Solution:

\begin{array}{l} \frac{2 + m}{2} = 5 \\ 2 + m = 10 \\ m = 8 \end{array}

Question 2:

In diagram below, P and Q are points on a Cartesian plane.

If M is the midpoint of PQ, then the coordinates of M are

Solution:

\begin{array}{l} P (- 4, 8), Q (6, - 2) \\ Coordinates of M \\ = (\frac{- 4 + 6}{2}, \frac{8 + (- 2)}{2}) \\ = (1, 3) \end{array}

Question 3:

Find the distance between P (–4, 6) and Q (20, –1).

Solution:

\begin{array}{l} Distance of P Q \\ = \sqrt{{(- 4 - 20)}^{2} + {[6 - (- 1)]}^{2}} \\ = \sqrt{{(- 24)}^{2} + 7^{2}} \\ = \sqrt{576 + 49} \\ = \sqrt{625} \\ = 25 units \end{array}

Question 4:

Diagram shows a straight line PQ on a Cartesian plane.

Calculate the length, in unit, of PQ.

Solution:

PS = 15 – 3 = 12 units

SQ = 8 – 3 = 5 units

By Pythagoras’ theorem,

PQ²= PS² + SQ²

= 12²+ 5²

PQ = √169

= 13 units

Question 5:

The diagram shows an isosceles triangle STU.

Given that ST = 5 units, the coordinates of point S are

Solution:

For an isosceles triangle STU, M is the midpoint of straight line TU.

\begin{array}{l} x - coordinate of M \\ = \frac{- 2 + 4}{2} = 1 \end{array}

Point M = (1, 0)

MT = 4 – 1 = 3 units

By Pythagoras’ theorem,

SM²= ST² – MT²

= 5² – 3²

= 25 – 9

= 16

SM = √16

= 4

Therefore, point S = (1, 4).

8.1 Coordinates

Posted on September 1, 2017 by user

8.1 Coordinates

8.1.1 Coordinates

1. The Cartesian coordinate system is a number plane with a horizontal line (x-axis) drawn at right angles to a vertical line (y-axis), intersecting at a point called origin.

2. It is used to locate the position of a point in reference to the x-axis and y-axis.

3. The coordinate of any point are written as an ordered pair (x, y). The first number is the x-coordinate and the second number is the y-coordinate of the point.

Example:

The coordinates of points A and B are (3, 4) and (–5, –2) respectively.

This means that point A is located 3 units from they-axis and 4 units from the x-axis, whereas point B is located 5 units on the left from the y-axis and 2 units from the x-axis.

4. The coordinate of the origin O is (0, 0).

8.1.2 Scales for the Coordinate Axes

1. The scale for an axis is the number of units represented by a specific length along the axes.

2. The scale on a coordinate is usually written in the form of a ratio.

Example:

A scale of 1 : 2 means one unit on the graph represents 2 units of the actual length.

3. Both coordinate axes on the Cartesian plane may have

(a) the same scales, or

(b) different scales.

Example:

1 unit on the x-axis represents 2 units.

1 unit on the y-axis represents 1 unit.

Therefore the scale for x-axis is 1 : 2 and the scale for y-axis is 1 : 1.

Coordinates of:

P (4, 3) and Q (10, 5).

8.1.3 Distance between Two Points

1. Finding the distance between two points on a Cartesian plane is the same as finding the length of the straight line joining them.

2. The distance between two points can be calculated by using Pythagoras’ theorem.

Example:

AB = 2 – (–4) = 2 + 4 = 6 units

BC = 5 – (–3) = 5 + 3 = 8 units

By Pythagoras’ theorem,

AC²= AB² + AC²

= 6² + 8²

AC = √100

= 10 units

3. Distance is always a positive value.

8.1.4 Midpoint

The midpoint of a straight line joining two points is the middle point that divides the straight line into two equal halves.

Midpoint, M = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})

Example:

The coordinate of the midpoint of (7, –5) and (–3, 11) are

\begin{array}{l} (\frac{7 + (- 3)}{2}, \frac{- 5 + 11}{2}) \\ = (\frac{4}{2}, \frac{6}{2}) \\ = (2, 3) \end{array}

7.2.3 Geometrical Constructions, PT3 Focus Practice

Posted on August 25, 2017 by user

Question 6:
Diagram below in the answer space shows part of a triangle ABC.

\begin{array}{l} (a) Using a pair of compasses, protractor and ruler, draw the \\ triangle A B C with A B = 7 cm, ∠ A B C = 65^{o} and B C = 5 cm . \\ (b) Measure ∠ A C B . \end{array}

Answer:
(a)

Solution:
(a)

(b)

∠ A C B = 72^{o}

Question 7:
Diagram below shows a quadrilateral ABQR.

(a) Using only a ruler and a pair of compasses, construct the diagram using the measurement given.
Begin from the straight lines AB and BQ provided in the answer space.
(b) Based on the diagram constructed in (a), measure the length, in cm, of QR.

Answer:
(a)