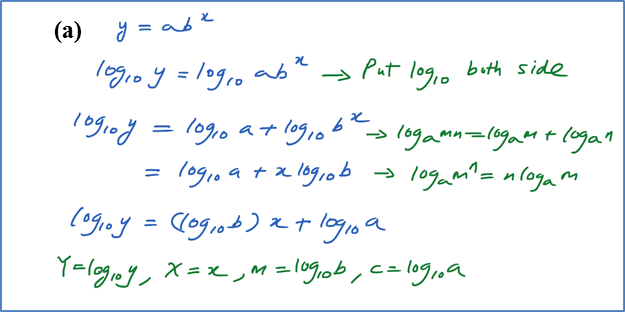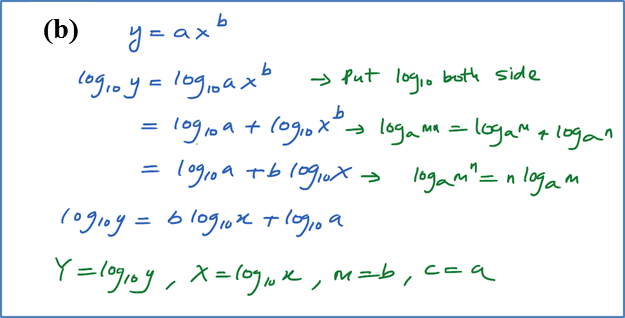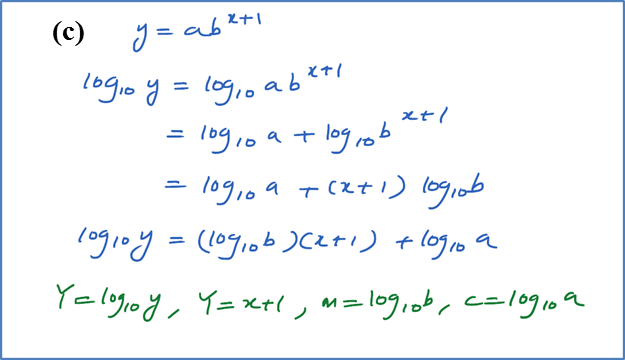2.7 Hukum Linear, SPM Praktis (Kertas 2)
Soalan 2:
Gunakan kertas graf untuk menjawap soalan ini.
Jadual di bawah menunjukkan nilai-nilai bagi dua pemboleh ubah x dan y, yang diperoleh daripada satu eksperimen. Pemboleh ubah x dan y dihubungkan oleh persamaan , dengan keadaan k dan p ialah pemalar.
|
x
|
1.5
|
2
|
3
|
4
|
5
|
6
|
|
y
|
5.004
|
1.540
|
0.930
|
0.770
|
0.705
|
0.656
|
(a)
Berdasarkan jadual di atas, bina satu jadual bagi nilai-nilai
(b)
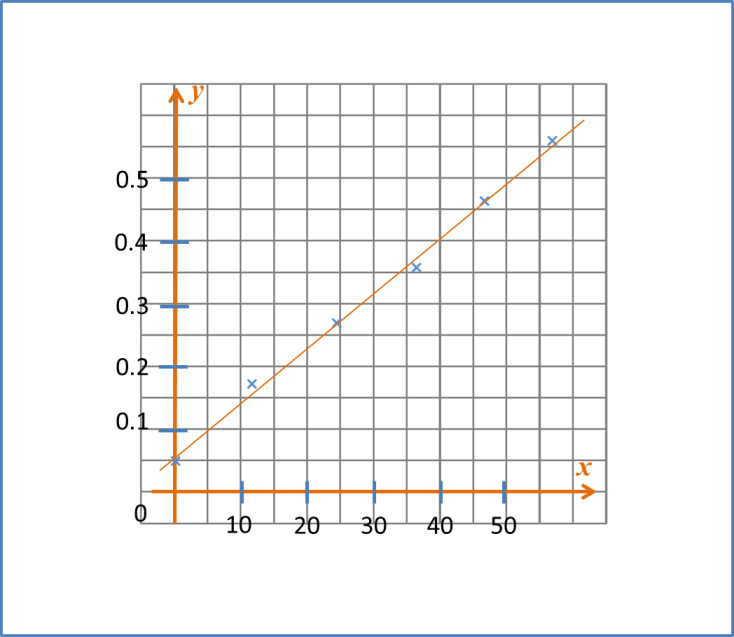
plot dengan menggunakan skala 2 cm kepada 0.1 unit pada paksi dan skala 2 cm kepada 0.2 unit pada paksi ,
Seterusnya, lukis garis lurus penyuaian terbaik.
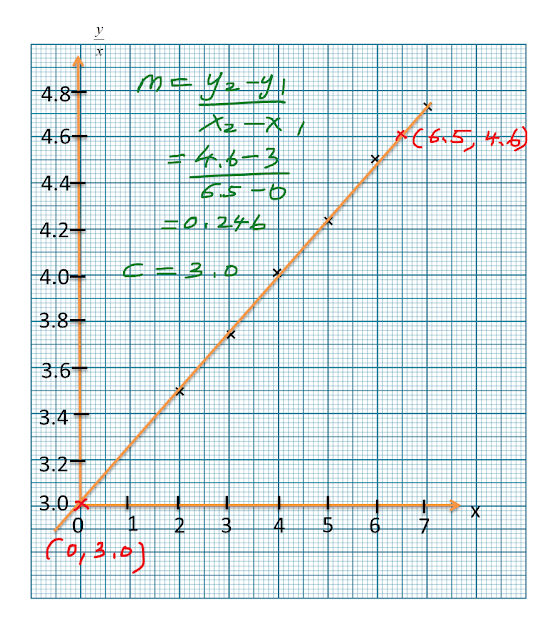
(c)
Gunakan graf di (b) untuk mencari nilai
(i)
a,
(ii)
b,
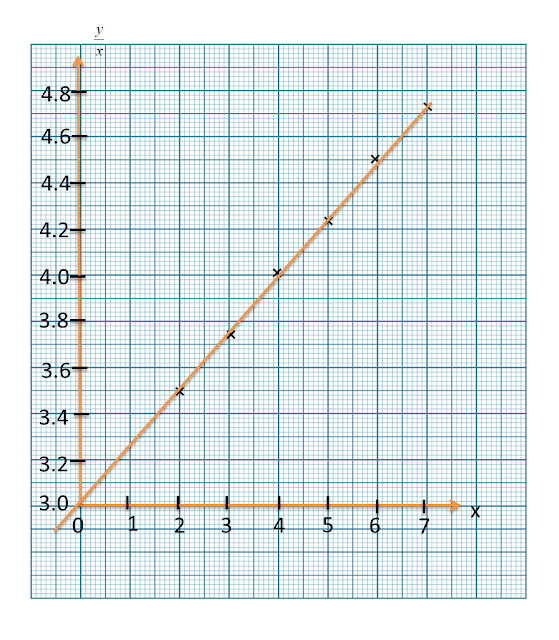
Penyelesaian:
(a)

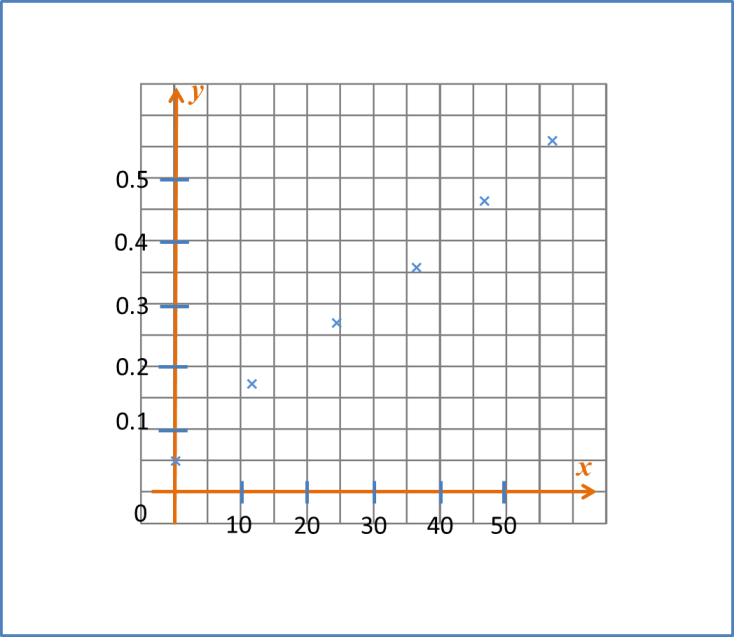
(b)
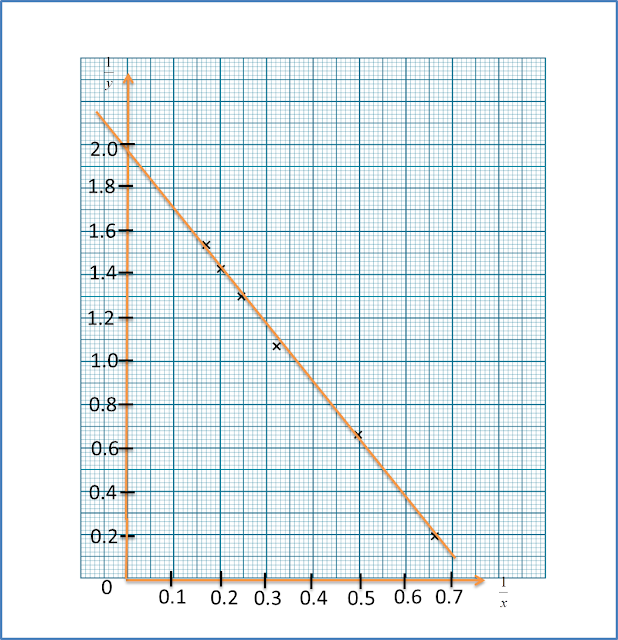
(c)(i)(ii)