Bab 19 Taburan Kebarangkalian

Posted on September 22, 2016 by user

8.3.2 Taburan Kebarangkalian, SPM Praktis (Kertas 1)

Soalan 3:

Jisim mangga di sebuah gerai mempunyai taburan normal dengan min 200g dan sisihan piawai 30g.

(a) Cari jisim, dalam g, sebiji mangga yang mempunyai skor-z bernilai 0.5.

(b) Jika sebiji mangga dipilih secara rawak, cari kebarangkalian bahawa mangga itu mempunyai jisim sekurang-kurangnya 194g.

Penyelesaian:

μ = 200g

σ = 30g

Katakan X ialah jisim sebiji mangga.

(a)

\frac{X - 200}{30} = 0.5

X = 0.5(30) + 200

X = 215g

(b)

P (X ≥ 194)

= P (Z \geq \frac{194 - 200}{30})

= P (Z ≥ –0.2)

= 1 – P (Z > 0.2)

= 1 – 0.4207

= 0.5793

Soalan 4:

Rajah di bawah menunjukkan satu graf taburan normal piawai.

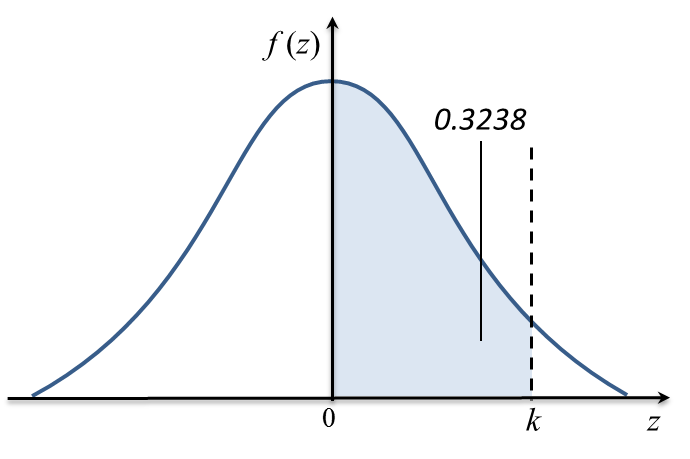
Kebarangkalian yang diwakili oleh luas kawasan berlorek ialah 0.3238.

(a) cari nilai k.

(b) X ialah pemboleh ubah rawak selanjar bertaburan secara normal dengan min 80 dan varians 9.

Cari nilai X apabila skor-z ialah k.

Penyelesaian:

(a)

P (Z > k) = 0.5 – 0.3238

= 0.1762

k = 0.93

(b)

μ = 80,

σ² = 9, σ = 3

\frac{X - 80}{3} = 0.93

X = 3 (0.93) + 80

X = 82.79

Bab 19 Taburan Kebarangkalian

Posted on September 22, 2016 by user

8.3.1 Taburan Kebarangkalian, SPM Praktis (Kertas 1)

Soalan 1:

Rajah di bawah menunjukkan graf suatu taburan binomial bagi X.

Cari

(a) nilai h,

(b) P (X ≥ 3)

Penyelesaian:

(a)

P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4) = 1

\begin{array}{l} \frac{1}{16} + \frac{1}{4} + h + \frac{1}{4} + \frac{1}{16} = 1 \\ h = 1 - \frac{5}{8} \\ h = \frac{3}{8} \end{array}

(b)

P (X ≥ 3) = P (X = 3) + P (X = 4)

P (X \geq 3) = \frac{1}{4} + \frac{1}{16} = \frac{5}{16}

Soalan 2:

Pembolehubah rawak X mewakili taburan binomial dengan 10 percubaan dan keberangkalian berjaya ialah ¼.

(a) sisihan piawai taburan itu,

(b) kebarangkalian bahawa sekurang-kurangnya satu percubaan adalah berjaya.

Penyelesaian:

(a)

n = 10, p = ¼

\begin{array}{l} Sisihan piawai = \sqrt{n p q} \\ = \sqrt{10 \times \frac{1}{4} \times \frac{3}{4}} \\ = 1.875 \end{array}

(b)

\begin{array}{l} P (X = r) = C_{r} {(\frac{1}{4})}^{r} {(\frac{3}{4})}^{10 - r} \\ P (X \geq 1) \\ = 1 - P (X < 1) \\ = 1 - P (X = 0) \\ = 1 - C_{0} {(\frac{1}{4})}^{0} {(\frac{3}{4})}^{10} \\ = 0.9437 \end{array}

Bab 10 Penyelesaian Segitiga

Posted on September 19, 2016 by user

Soalan 4:

Dalam rajah di bawah, ABC ialah sebuah segi tiga. AGJB, AHC dan BKC ialah garis lurus. Garis lurus JK adalah berserenjang kepada BC.

Diberi bahawa BG = 40cm, GA = 33 cm, AH = 30 cm, GAH = 85^o dan JBK = 45^o.
(a) Hitung panjang, dalam cm, bagi

i. GH

ii. HC

(b) Luas segi tiga GAH adalah dua kali luas segi tiga JBK. Hitung panjang, dalam cm, bagi BK.

(c) Lakar segi tiga A’B’C’ yang mempunyai bentuk yang berlainan daripada segi tiga ABC dengan keadaan A’B’ = AB, A’C’ = AC dan ∠ A’B’C’ = ∠ ABC.

Penyelesaian:

(a)(i)

Guna petua kosinus,

GH² = AG² + AH² – 2 (AG)(AH) kos ∠ GAH

GH²= 33²+ 30² – 2 (33)(30) kos 85^o

GH² = 1089 + 900 – 172.57

GH² = 1816.43

GH = 42.62 cm

(a)(ii)

∠ ACD = 180^o – 45^o– 85^o= 50^o

Guna petua sinus,

\begin{array}{l} \frac{A C}{\sin 45^{\circ}} = \frac{73}{\sin 50^{\circ}} \\ A C = \frac{73 \times \sin 45^{\circ}}{\sin 50^{\circ}} \end{array}

AC = 67.38 cm

Oleh itu, HC = 67.38 – 30 = 37.38 cm

(b)

Area of ∆ GAH = ½ (33)(30) sin 85^o = 493.12 cm²

Katakan panjang BK = JK = x

2 × Area of ∆ JBK = Area of ∆ GAH

2 × [½ (x)(x)] = 493.12

x² = 493.12

x = 22.21 cm
BK = 22.21 cm

(c)

Bab 10 Penyelesaian Segitiga

Posted on September 19, 2016 by user

Soalan 3:

Rajah di bawah menunjukkan sebuah segi tiga ABC.

(a) Hitungkan panjang, dalam cm, bagi AC.

(b) Suatu sisi empat ABCD dibentuk dengan keadaan AC ialah pepenjuru, ∠ACD = 45° dan AD = 14 cm.

Hitung dua nilai yang mungkin bagi ∠ADC.

(c) Dengan menggunakan ∠ADC yang tirus dari (b), hitungkan
i. panjang, dalam cm, bagi CD,
ii. luas, dalam cm², sisi empat ABCD itu

Penyelesaian:

(a)

Guna petua kosinus,

AC² = AB² + BC² – 2 (AB)(BC) kos ∠ABC

AC² = 16² + 12² – 2 (16)(12) kos 70^o

AC² = 400 – 131.33

AC² = 268.67

AC = 16.39 cm

(b)

\begin{array}{l} Guna petua sinus, \\ \frac{\sin ∠ A D C}{16.39} = \frac{\sin 45^{\circ}}{14} \\ \sin ∠ A D C = \frac{16.39 \times \sin 45^{\circ}}{14} \end{array}

sin ∠ ADC = 0.8278

∠ ADC = 55.87^o atau (180^o – 55.87^o)

∠ ADC = 55.87^o atau 124.13^o

(c)(i)

sudut tirus ADC = 55.87^o

∠ CAD = 180^o – 45^o – 55.87^o= 79.13^o

\begin{array}{l} \frac{C D}{\sin {79.13}^{\circ}} = \frac{14}{\sin 45^{\circ}} \\ C D = \frac{14 \times \sin {79.13}^{\circ}}{\sin 45^{\circ}} = 19.44 cm \end{array}

(c)(ii)

Luas sisi empat ABCD

= Luas ∆ ABC + Luas ∆ ACD

= ½ (16)(12) sin 70^o+ ½ (16.39)(14) sin79.13^o

= 90.21 + 112.67

= 202.88 cm²

3.7.1 The Role of Human Nervous System (Structured Question 1 & 2)

Posted on September 2, 2016 by user

Question 1:
Diagram below shows a cross-section of part of the nervous system.

(a)(i) Name structure P.

(a)(ii) State the function of P.

(b)(i) Why is Q swollen at the dorsal root?

(b)(ii) Complete the Diagram with the neurones involved in a reflex action. Mark the direction of the impulse movement on the neurones.

(c) Compare two structures of a sensory neurone and a motor neurone.

(d) If the spinal nerve is cut off at R, what is the effect on the organ which is connected to it?
Explain your answer.

(e) Azmin’s finger accidentally touches a flame.
Explain briefly how his reflex action functions to avoid the injury.

Answer:
(a)(i)
P : Spinal cord

(a)(ii)
Function of P : Controls reflex actions.

(b)(i)
To place the cell bodies of the afferent neurones.

(b)(ii)

(c)

(d)
The organ is unable to respond. Impulses cannot flow to the effector.

(e)
- The receptor detects heat and triggers an impulse.
- The impulse is sent to the spinal cord through the afferent neurone.
- The impulse flows through the afferent neurone which synapses with the interneurone and then synapses with the efferent neurone.
- The efferent neurone sends an impulse to the effector.
- The hand is pulled away from flame.

Ethylene

Posted on August 10, 2016 by user

Ethylene

1. Ethylene is a small hydrocarbon gas.

2. It is a plant hormone which is synthesized during the ripening of fruits.

3. Ethylene is responsible for the changes in texture, softening, color, and other processes involved in ripening.

4. Ethylene
(a) Speeds up the ripening of fruits by stimulating the production of cellulose. Cellulase hydrolyses the cellulose in plant cell walls, making the fruit soft.
(b) Promotes the breakdown of complex carbohydrate into simple sugar. This make ripe fruit tastes sweeter than an unripe fruit.

5. Ethylene gas is used commercially to ripen tomatoes, bananas and pears.

3.6 Plant Hormones

Posted on August 2, 2016 by user

3.6 Plant Hormones

1. Growth of shoots towards sunlight is called positive phototropism.

2. Growth of shoots away from sunlight is called negative phototropism.

3. In plants, hormones play an important role in growth processes such as seed germination, growth of roots and development of fruits.

4. There are many types of plant hormones, such as auxins and ethylene.

Effects of Auxins on Growth Responses

1. Auxins are produced in the apical meristems of the shoot tip and the root tip in the cell division zone.

2. In the shoot tip, high concentrations of auxins stimulate cell elongation.

3. The effect of high concentrations of auxins in the root tip is different from that in the shoot tip. In the root tip, a high concentration of auxins inhibits cell elongation.

3.4.1 The human kidney

Posted on July 18, 2016 by user

The Excretory System

1. The excretory system plays an important role in homeostasis.

2. The primary organs of the excretory system are kidneys.

The human kidney

1. The kidneys filter blood and form urinewhich exits the body through the ureters, urinary bladder and urethra.

2.Urine is fluid which consists of water, urea and other dissolved wastes.

3.The human kidney shows three distinct regions

(a) Cortex(outer light-red region)

(b) Medulla(inner dark-red region)

(c) Pelvis(central cavity in which the ureter directly connects to)

The Nephron

1. Each kidney consists of millions of microscopic tubules called nephron.

2. A nephron consists of three major parts:

(a) the glomerulus

(b) the Bowman’s capsule, and

(c) renal tubule

3. The renal tubule is made up of the

(a) proximal convoluted tubule

(b) loop of Henle

(c) distal convoluted tubule

3.4 Homeostasis in Humans

Posted on July 16, 2016 by user

3.4 Homeostasis in Humans

1. The internal environment consists of interstitial fluid and blood plasma that constantly bathe the cells.

2. Homeostasis is the process of regulating the physical and chemical factors in the internal environment, so that these factors can be maintained in a dynamic equilibrium and optimum condition.

(a) The physical factors include body temperature, blood pressure and osmotic pressure.

(b) The chemical factors in the blood include partial pressure of oxygen and carbon dioxide, and the salt and sugar levels.

Bab 17 Pilir Atur dan Gabungan

Posted on July 11, 2016 by user

6.2 Gabungan

1. Bilangan gabungan r objek daripada n objek

^{n} C_{r} = \frac{n!}{r! (n - r)!}

2. Bilangan gabungan r objek daripada n objek yang berlainan ialah bilangan pilihan r objek daripada n objek dengan tanpa mengambil kira tertib susunan.

\begin{array}{l} Peringatan: \\ (i)^{n} C_{0} = 1 \\ (i i)^{n} C_{n} = 1 \\ (i i i)^{n} C_{r} =^{n} C_{n - r} \end{array}

Contoh 1:

\begin{array}{l} {Hitung nilai}^{7} C_{2} \\ ^{7} C_{2} = \frac{7!}{(7 - 2)! \times 2!} \\ = \frac{7!}{5! \times 2!} \\ = \frac{7 \times 6 \times 5!}{5! \times 2!} \\ = \frac{7 \times 6}{2 \times 1} \\ = 21 \end{array}

Contoh 2:

6 biji guli yang mempunyai warna yang berbeza akan dibahagikan sama rata kepada 2 orang kanak-kanak. Cari bilangan cara pembahagian guli tersebut dapat dibuat.

Penyelesaian:

Bilangan cara memberi 3 biji guli kepada kanak-kanak pertama =

^{6} C_{3}

Bilangan cara memberi baki 3 biji guli kepada kanak-kanak kedua =

^{3} C_{3}

Bilangan cara pembahagian guli sama rata kepada 2 orang kanak-kanak

\begin{array}{l} =^{6} C_{3} \times^{3} C_{3} \\ = 20 \times 1 \\ = 20 \end{array}