9.3.2 Trigonometri II, SPM Praktis (Kertas 1)
Soalan 4:
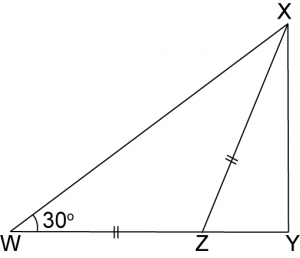
Dalam rajah di atas, WZY ialah satu garis lurus. ∠XYZ = 90o, ∠XWZ = 30o dan WZ = XZ = 30cm. Cari panjang XY.
Penyelesaian:
∠WXZ = ∠XWZ = 30o
Maka ∠XZY = 30o + 30o = 60o
XY= sin 60o × 30
XY = 25.98cm
Soalan 5:
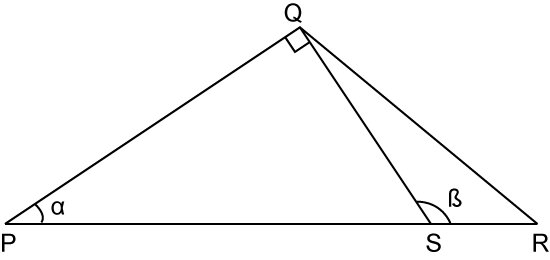
Dalam rajah di atas, PQS ialah satu segitiga bersudut tegak. Diberi bahawa SR = 6cm, PQ = 12 cm dan 5SR = 2PS. Cari nilai cos α dan tan β.
Penyelesaian:
Dalam ∆ PQS, guna Teori Pythagoras,
Soalan 6:
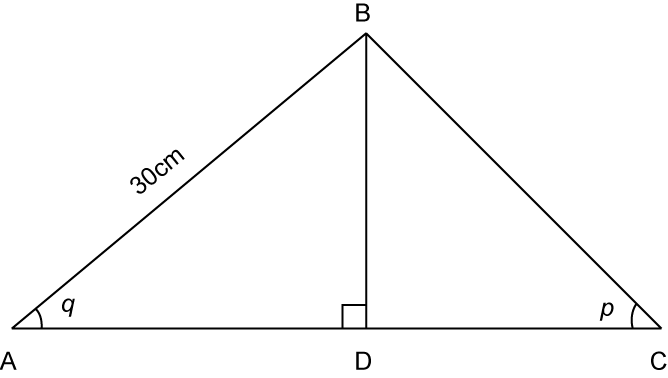
Dalam rajah di atas, ADC ialah satu garis lurus,
. Hitung jarak AC.
Penyelesaian:
Dalam ∆ ABD, guna Teori Pythagoras,
Oleh itu, jarak AC = 24 + 36 = 60cm