5.6.2 Garis Lurus, SPM Praktis (Soalan Pendek)
Soalan 6:
Rajah di bawah menunjukkan suatu garis lurus RS dengan persamaan 3y = –px– 12, dengan p sebagai pemalar.
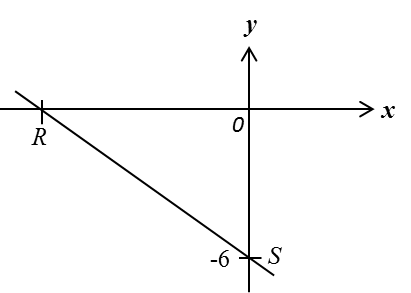

Diberi bahawa OR: OS = 3 : 2.
Cari nilai p.
Penyelesaian:
Kaedah 1:
Gantikan x = –6 dan y = 0 ke dalam 3y = –px– 12:
3(0) = –p (–6) – 12
0 = 6p – 12
–6p = –12
p = 2
Kaedah 2:
OR: OS = 3 : 2
Koordinat titik S = (0, –4)
Kecerunan garis lurus RS =
Diberi 3y = –px – 12
Menyusun semula persamaan dalam bentuk y = mx+ c
Soalan 7:
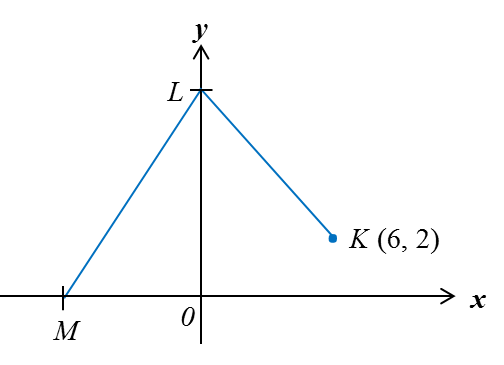
Rajah di atas menunjukkan dua garis lurus, KL dan LM, pada satah Cartesan. Jarak KL ialah 10 unit dan kecerunan bagi LM ialah 2. Cari pintasan-x bagi LM.
Penyelesaian:
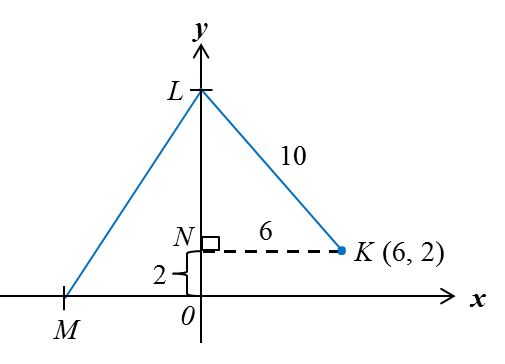
Guna rumus Pythagoras,
LN = √102 – 62 = 8
Titik L = (0, 2 + 8) = (0, 10)
pintasan-y bagi LM = 10
pintasan-y bagi LM = 10