Bab 1 Fungsi

Posted on June 1, 2016 by user

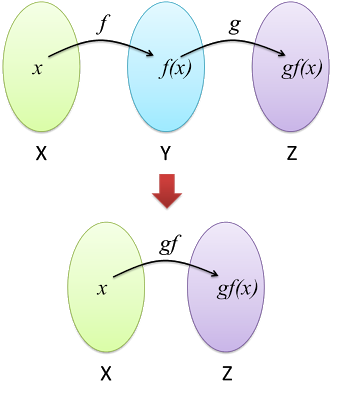
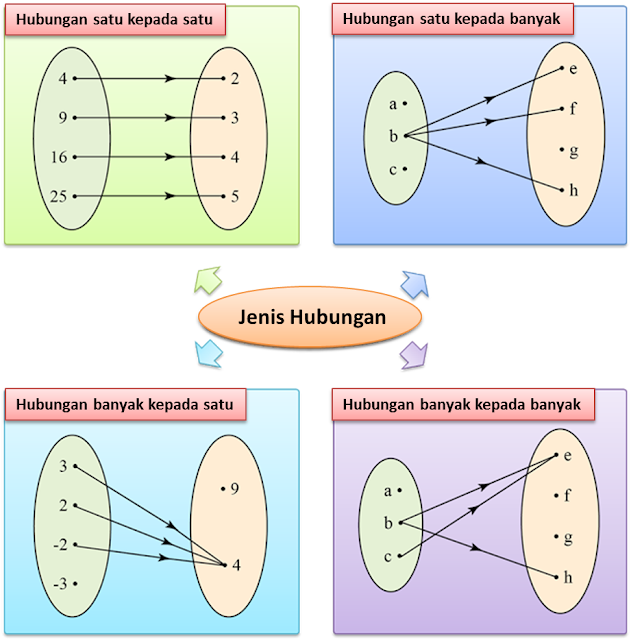
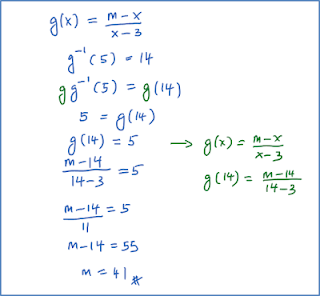1.1a Domain and Kodomain

Dalam hubungan antara satu set dengan set yang lain, set pertama dikenali sebagai domain dan set kedua dikenali sebagai kodomain.
Unsur-unsur dalam domain dinamakan objek, manakala unsur-unsur dalam kodomain dipadankan dengan objek dinamakan imej.
Unsur-unsur dalam kodomain tidak dipadankan dengan objek adalah bukan imejnya.
Semua imej dalam kodomain boleh ditulis sebagai satu set dinamakan julat.

Contoh:

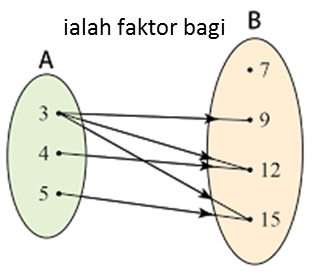
Domain = {3, 4, 5}

Kodomain = {7, 9, 12, 15}

Julat = {9, 12, 15} [7 bukan satu imej kerana ia tidak dipadankan dengan sebarang objek]

3 ialah objek bagi 9, 12 dan 15.

4 ialah object bagi 12.

5 ialah object bagi 15.

9, 12 dan 15 ialah imej bagi 3.

12 ialah imej bagi 4.

15 ialah imej bagi 5.

Bab 1 Fungsi

Posted on May 19, 2016 by user

1.4 Fungsi Songsangan

Untuk mencari fungsi songsangan, f ⁻¹ (x) atau f (x)
• Letakkan fungsi sama dengan y.
• Susun semula untuk menjadikan x dalam sebutan y.
• Tulis semula f ⁻¹ (x) dengan menggantikan y oleh x.

Contoh 1:

Diberi f (x) = 5x − 4, cari fungsi songsangan.

Penyelesaian:

Contoh 2:

Cari fungsi songsangan bagi setiap fungsi yang berikut

(a) f (x ) → 4 – 7x

$(b) f (x) = \frac{2 x + 5}{3}$

Penyelesaian:

Contoh 3:

Cari fungsi songsangan bagi setiap fungsi yang berikut

$\begin{array}{l} (a) f (x) = \frac{5}{7 x} \\ (b) f (x) = \frac{2}{3 - x} \end{array}$

Penyelesaian:

Bab 1 Fungsi

Posted on May 19, 2016 by user

1.3d Cari Fungsi Baru dengan Menggunakan Fungsi Gubahan yang diberi(Kes B : Fungsi kedua diberi) Soalan susah. Pastikan anda cuba!

Contoh 1 (Kaedah Penggantian):

Suatu fungsi f ditakrifkan oleh f : x → x + 2.
Cari fungsi g jika gf: x → x²+ 3x + 5.
[ Perhatian: Fungsi kedua f diberi, gantikan y = x + 2]

Penyelesaian:

Contoh 2 (Kaedah Penggantian):

Suatu fungsi f ditakrifkan oleh f : x → x – 1.
Cari fungsi g jika

$g f : x \to \frac{4}{x + 2}, x \neq - 2.$
[Perhatian: Fungsi kedua f diberi, gantikan y = x – 1]

Penyelesaian:

Bab 1 Fungsi

Posted on May 19, 2016 by user

1.3c Cari Fungsi Baru dengan Menggunakan Fungsi Gubahan yang diberi (kes A : Fungsi pertama diberi)

Contoh 1:

Suatu fungsi f ditakrifkan oleh f : x → 2x + 5 .
Cari fungsi g jika fg : x → 3x − 8 .
[Perhatian: Fungsi pertama f diberi]

Penyelesaian:

Contoh 2:

Suatu fungsi f ditakrifkan oleh

$f : x \to \frac{2}{x} .$
Cari fungsi g jika fg : x → x ² + 1 .
[Perhatian: Fungsi pertama f diberi]

Penyelesaian:

Bab 1 Fungsi

Posted on May 19, 2016 by user

1.3b Fungsi Gubahan (Kaedah Perbandingan) Contoh Soalan

Contoh 1:

Diberi f : x → hx + k, g : x → (x + 1)² + 4 dan fg : x→ 2(x + 1)² + 5. Cari
(a) nilai g ² (2),
(b) nilai h dan nilai k.

Penyelesaian:

Contoh 2:

Diberi f : x → 1 – x dan g : x → px² + q. Jika fungsi gubahan gf ditakrifkan oleh gf : x→ 3x²– 6x + 5, cari
(a) nilai p dan nilai q,
(b) nilai g ² (−1).

Penyelesaian:

Bab 1 Fungsi

Posted on May 18, 2016 by user

1.3a Fungsi Gubahan

Jika fungsi f : X → Y,

dan fungsi g : Y → Z,

maka, fungsi gubahan gf: X → Z

Soalan 1:

Diberi fungsi f : x → 2x + 5 dan g : x→ x² – 1, cari gf (2)

Penyelesaian:

f (x) = 2x + 5

f (2) = 2(2) + 5 = 9

gf (2) = g [f (2)] = g (9)

g(x) = x²– 1

gf(2) = g(9) = 9² – 1 = 80

Soalan 2:

Jika f : x → x + 5 dan g : x → x² + 2x + 3, cari
(a) nilai gf (2),
(b) nilai fg (2 ),
(c) fungsi gubahanfg,
(d) fungsi gubahan gf,
(e) fungsi gubahan g²,
(f) fungsi gubahan f ².

Penyelesaian:

Pembetulan bagi (c)

$\begin{array}{l} f g (x) = f (x^{2} + 2 x + 3) \\ = (x^{2} + 2 x + 3) + 5 \\ = x^{2} + 2 x + 3 + 5 \\ = x^{2} + 2 x + 8 \end{array}$

Pembetulan bagi (e)

$\begin{array}{l} g^{2} (x) = g g (x) \\ = g (x^{2} + 2 x + 3) \\ = {(x^{2} + 2 x + 3)}^{2} + 2 (x^{2} + 2 x + 3) + 3 \\ = x^{4} + 2 x^{3} + 3 x^{2} + 2 x^{3} + 4 x^{2} + 6 x \\ + 3 x^{2} + 6 x + 9 \\ = x^{4} + 4 x^{3} + 10 x^{2} + 12 x + 9 \end{array}$

Bab 1 Fungsi

Posted on May 18, 2016 by user

1.1c Jenis Hubungan

1. Hubungan boleh dikelaskan kepada 4 jenis, iaitu:

(a) Hubungan satu kepada satu

(b) Hubungan satu kepada banyak

(c) Hubungan banyak kepada satu

(d) Hubungan banyak kepada banyak

Bab 1 Fungsi

Posted on May 15, 2016 by user

1.5 Fungsi, SPM Praktis (Soalan Pendek)

Soalan 10:

Jika

$g : x \to \frac{m - x}{x - 3}, x \neq 3$ dan g ⁻ ¹ (5) = 14. Cari nilai m.

Penyelesaian:

Soalan 11 (Kaedah Bandingan):

$Jika f : x \to \frac{m x - n}{x - 2}, x \neq 2 dan f^{- 1} : x \to \frac{5 - 2 x}{2 - x}, x \neq 2.$ Cari nilai m dan n.

Penyelesaian:

$\begin{array}{l} f (x) = \frac{m x - n}{x - 2} \\ Katakan y = \frac{m x - n}{x - 2} \to cari f^{- 1} (x) \\ y (x - 2) = m x - n \\ x y - 2 y = m x - n \\ x y - m x = 2 y - n \to \begin{array}{l} pindah x ke \\ sebelah kiri \end{array} \end{array}$

$\begin{array}{l} x (y - m) = 2 y - n \\ x = \frac{2 y - n}{y - m} \\ f^{- 1} (x) = \frac{2 x - n}{x - m} \\ \frac{2 x - n}{x - m} = \frac{5 - 2 x}{2 - x} \to \begin{array}{l} bandingkan dengan \\ f^{- 1} (x) yang diberi \end{array} \\ \times \frac{- 1}{- 1} \frac{n - 2 x}{m - x} = \frac{5 - 2 x}{2 - x} \\ maka, n = 5, m = 2 \end{array}$

Soalan 12 (Kaedah Bandingan):

Diberi bahawa

$f : x \to \frac{2 h}{x - 3 k}, x \neq 3 k,$ dengan keadaan h dan k ialah pemalar dan

$f^{- 1} : x \to \frac{14 + 24 x}{x}, x \neq 0.$ Cari nilai h dan k .

Penyelesaian:

$\begin{array}{l} f (x) = \frac{2 h}{x - 3 k} \\ Katakan y = \frac{2 h}{x - 3 k} \to cari f^{- 1} (x) \\ y (x - 3 k) = 2 h \\ x y - 3 k y = 2 h \\ x y = 2 h + 3 k y \\ x = \frac{2 h + 3 k y}{y} \end{array}$

$\begin{array}{l} f^{- 1} (x) = \frac{2 h + 3 k x}{x} \\ \frac{2 h + 3 k x}{x} = \frac{14 + 24 x}{x} \to \begin{array}{l} bandingkan dengan \\ f^{- 1} (x) yang diberi \end{array} \\ 2 h = 14 3 k = 24 \\ h = 7 k = 8 \end{array}$

Bab 1 Fungsi

Posted on May 14, 2016 by user

1.5 Fungsi, SPM Praktis (Soalan Pendek)

Soalan 8:

Cari fungsi songsangan

$f (x) = \frac{3 x + 2}{5 x + 3}$

Penyelesaian:

$\begin{array}{l} f (x) = \frac{3 x + 2}{5 x + 3} \\ katakan y = \frac{3 x + 2}{5 x + 3} \\ y (5 x + 3) = 3 x + 2 \\ 5 x y + 3 y = 3 x + 2 \\ 5 x y - 3 x = 2 - 3 y \\ x (5 y - 3) = 2 - 3 y \\ x = \frac{2 - 3 y}{5 y - 3} \\ f^{- 1} (x) = \frac{2 - 3 x}{5 x - 3} \to \begin{array}{l} tukar y kepada x \\ untuk cari f^{- 1} (x) \end{array} \end{array}$

Soalan 9:

(a) Jika f : x → x – 2, cari f ^-1 (5),

$(b) Jika f : x \to \frac{x + 9}{x - 5}, x \neq 5, cari f^{- 1} (3) .$

Penyelesaian:

(a)

f (x) = x– 2

Katakan y = f ^-1(5)

f (y) = 5

y – 2 = 5

y = 7

oleh itu, f ^-1(5) = 7

(b)

$\begin{array}{l} f (x) = \frac{x + 9}{x - 5} \\ katakan y = f^{- 1} (3) \\ f (y) = 3 \\ \frac{y + 9}{y - 5} = 3 \\ y + 9 = 3 y - 15 \\ 2 y = 24 \\ y = 12 \\ ∴ f^{- 1} (3) = 7 \end{array}$