Soalan 12:
(a) Didapati bahawa 60% murid dari sebuah kelas tertentu mendapat gred A bagi Bahasa Inggeris dalam peperiksaan percubaan O level.
Jika 10 orang murid dari kelas itu dipilih secara rawak, cari kebarangkalian bahawa
(i) tepat 7orang murid mendapat gred A.
(ii) tidak lebih daripada 7 orang murid mendapat gred A.
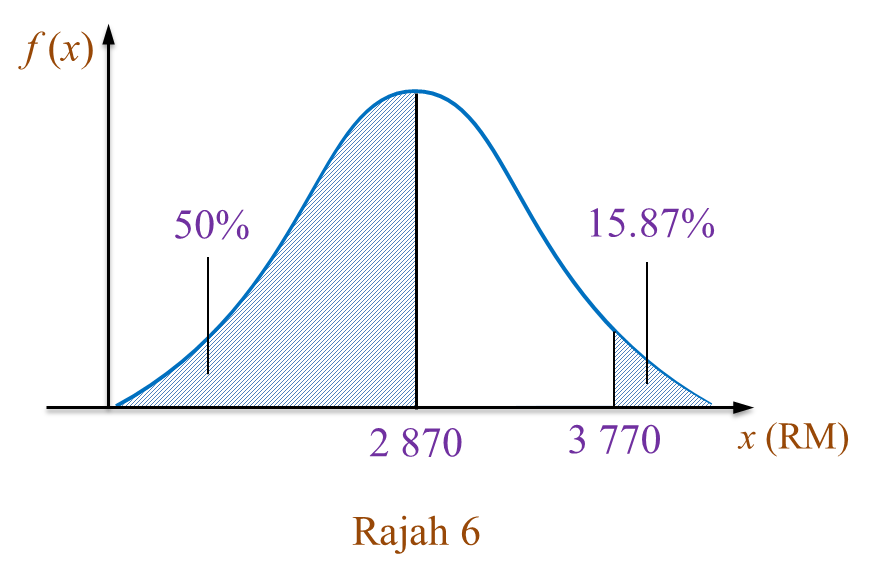
(b) Rajah di bawah menunjukkan satu graf taburan normal piawai yang mewakili isi padu kicap dalam botol yang dihasilkan oleh sebuah kilang.
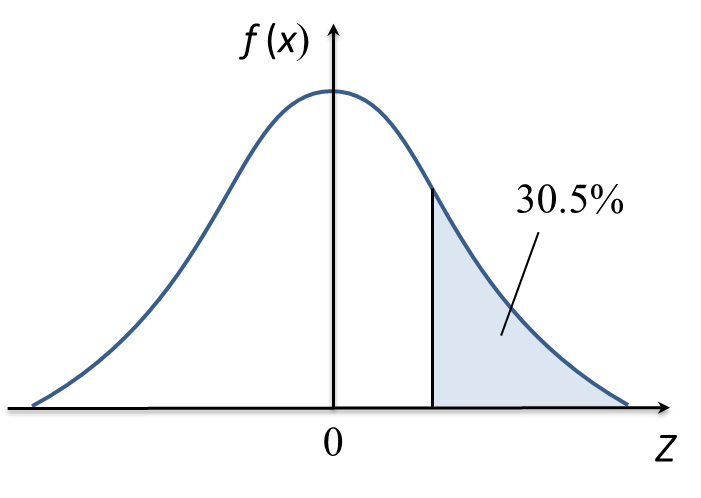
(b)(i)P(X>V)=30.5%P(Z>V−95016)=0.305P(Z>0.51)=0.305 V−95016=0.51V=0.51(16)+950 =958.16 cm3
(ii)Kebarangkalian=P(930<X<960)=P(930−95016<Z<960−95016)=P(−1.25<Z<0.625)=1−P(Z>1.25)−P(Z>0.625)=1−0.1056−0.2660=0.6284
(a) Didapati bahawa 60% murid dari sebuah kelas tertentu mendapat gred A bagi Bahasa Inggeris dalam peperiksaan percubaan O level.
Jika 10 orang murid dari kelas itu dipilih secara rawak, cari kebarangkalian bahawa
(i) tepat 7orang murid mendapat gred A.
(ii) tidak lebih daripada 7 orang murid mendapat gred A.
(b) Rajah di bawah menunjukkan satu graf taburan normal piawai yang mewakili isi padu kicap dalam botol yang dihasilkan oleh sebuah kilang.

Diberi bahawa min ialah 950 cm3 dan variansnya ialah 256 cm6. Jika peratus isi padu yang melebihi V ialah 30.5%, cari
(i) nilai V,
(ii) kebarangkalian bahawa isi padu antara 930 cm3 dan 960 cm3.
Penyelesaian:
(b)(i)P(X>V)=30.5%P(Z>V−95016)=0.305P(Z>0.51)=0.305 V−95016=0.51V=0.51(16)+950 =958.16 cm3
(ii)Kebarangkalian=P(930<X<960)=P(930−95016<Z<960−95016)=P(−1.25<Z<0.625)=1−P(Z>1.25)−P(Z>0.625)=1−0.1056−0.2660=0.6284

 Rajah
Rajah  Rajah
Rajah Rajah
Rajah