Bab 16 Fungsi Trigonometri

Posted on by
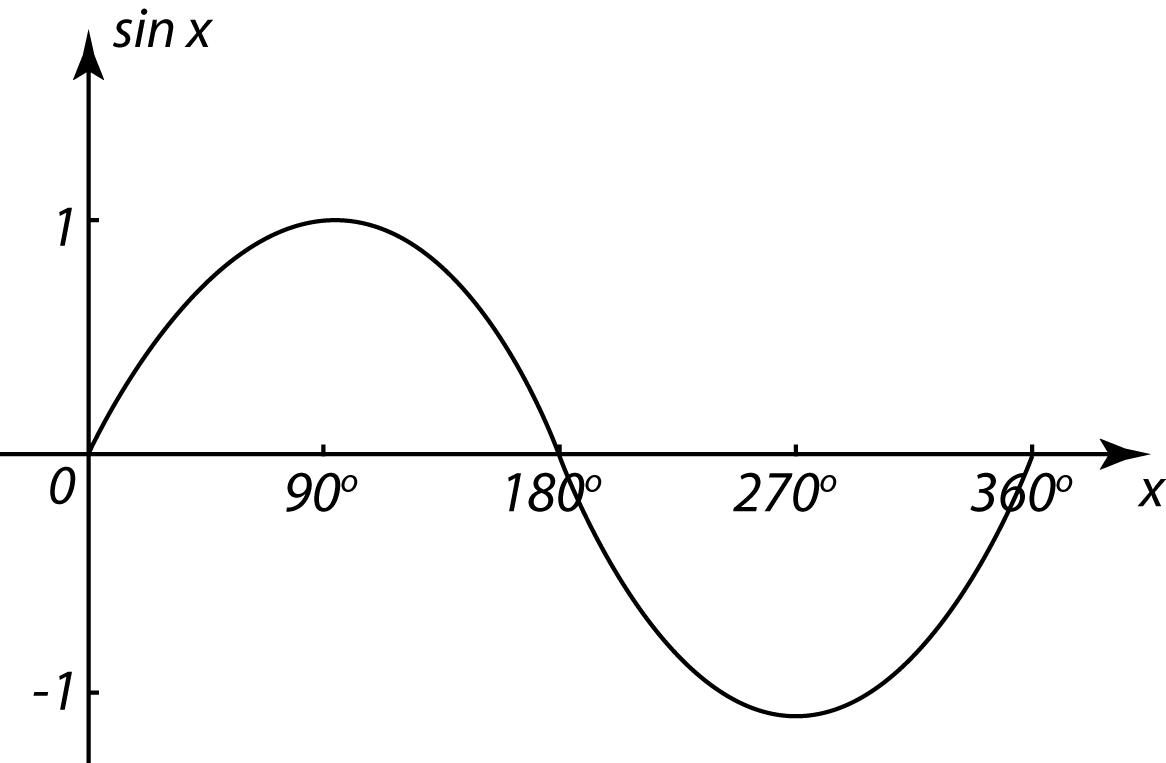
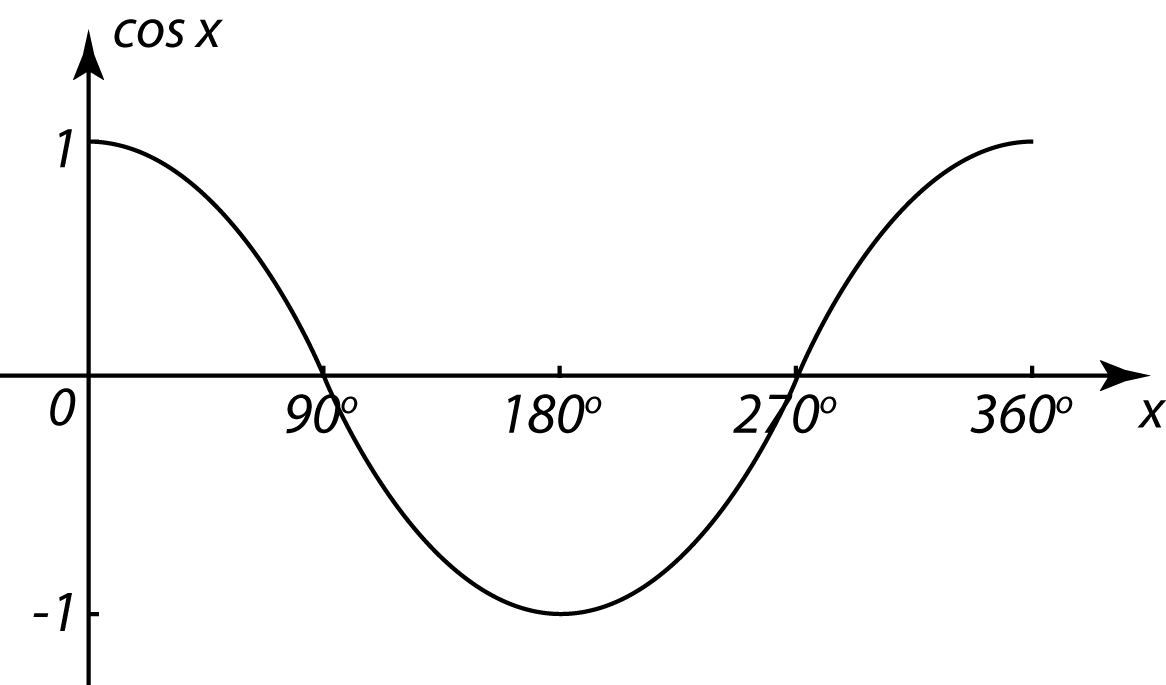
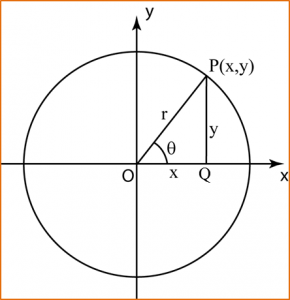
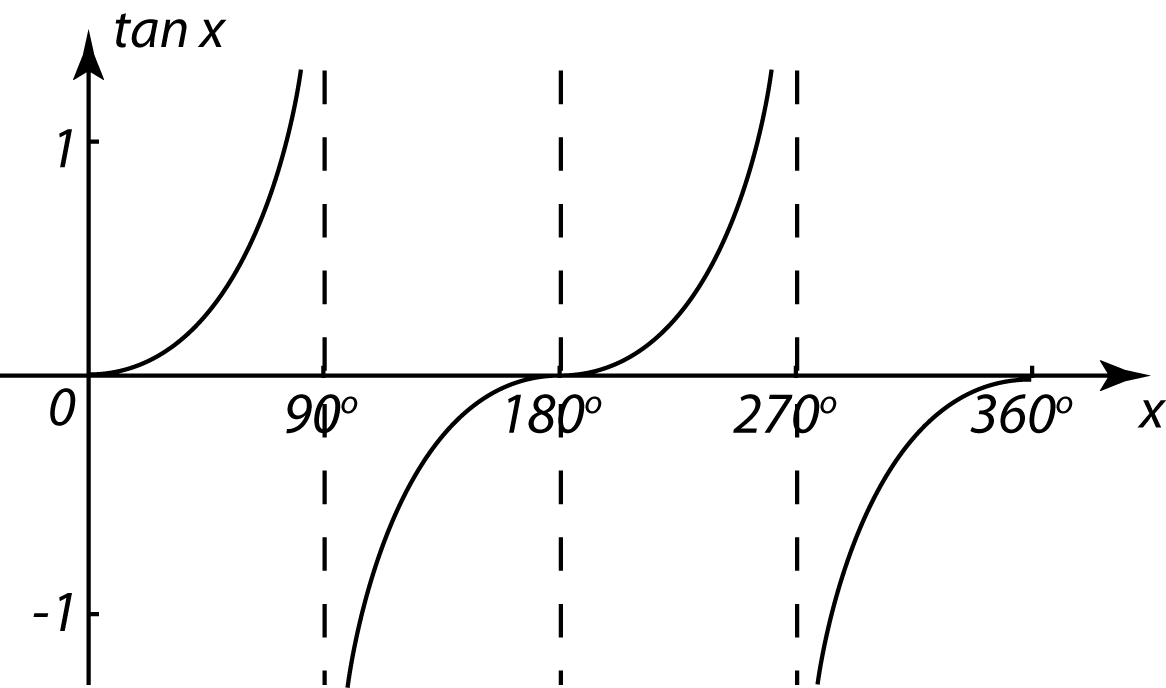5.6.4 Menyelesaikan Persamaan Trigonometri (Melibatkan Rumus Penambahan dan Rumus bagi Sudut Berganda)

Contoh 1 (Rumus penambahan):
Selesaikan persamaan yang berikut untuk 0o ≤ x ≤ 360o:
(a)    sin ( x – 25o) = 3 sin ( x + 25o)
(b)   3 kos (2x + 10o) = 2  

Penyelesaian:
(a)
sin ( x – 25o) = 3 sin ( x + 25o)  
sin x kos 25o – kos x sin 25o = 3 (sin x kos 25o + kos x sin 25o)
sin x kos 25o – kos x sin 25o = 3 sin x kos 25o + 3 kos x sin 25o
– sin x kos 25o = 4 kos x sin 25o
sinx kosx =− 4sin 25 ∘ 2kos 25 ∘  
tan x = – 2 tan 25o
tan x = – 2 (0.4663)
tan x = – 0.9326
Sudut asas x = 43o

Sudut yang dirujuk x = 43o berada di sukuan kedua dan keempat.
Oleh itu, x = 180o – 43o, 360o – 43o
x = 137o , 317o

(b)
3 kos (2x + 10o) = 2   ← (Ambil julat sudut dalam 0o ≤ x ≤ 720o, bagi 2 putaran lengkap)
kos ( 2x + 10o) = ⅔
Sudut asas ( 2x + 10o) = 48.19o
2x + 10o = 48.19o, 360o – 48.19o , 360o + 48.19o, 720o – 48.19o 
2x + 10o = 48.19o, 311.81o , 408.19o, 671.81o
2x = 38.19o, 301.81o , 398.19o, 661.81o
x = 19.10o, 150.91o , 199.10o, 330.91o


Contoh 2 (Rumus sudut berganda):
Cari semua sudut yang memuaskan 5 kos 2A + 9 sin A = 7, 0° < A < 360°.

Penyelesaian:
5 kos 2A + 9 sin A = 7
5 (1 – 2 sin2A) + 9 sin A = 7  ← (ganti kos 2A = 1 – 2sin2 A, seluruh persamaan sekarang dalam sebutan sin A)
5 – 10 sin2A + 9 sin A – 7 = 0
– 10 sin2A + 9 sin A – 2 = 0
10 sin2A – 9 sin A + 2 = 0
(2 sin A – 1)(5 sin A – 2) = 0
sin A = ½ = 0.5       atau      sin A = 2 5   = 0.4

Apabila sin A = 0.5,         
Sudut asas A = 30º
A = 30º, 180º – 30º
A = 30º, 150º

Apabila sin A = 0.4,         
Sudut asas A = 23.58º
A = 23.58º, 180º – 23.58º
A = 23.58º, 156.42º

Oleh itu A = 23.58º, 30º, 150º, 156.42º.


Contoh 3 (Rumus sudut berganda):
Cari semua sudut θ antara 0 dan 2π rad yang memuaskan persamaan sin 2θ = sin θ

Penyelesaian:
sin 2θ = sin θ
2 sin θ kos θ = sin θ   ←  (sin 2θ = 2 sin θ kos θ)
2 sin θ kosθ – sin θ = 0
sin θ (2 kos θ – 1) = 0   ← (Pemfaktoran)
sin θ = 0       atau      2 kos θ – 1 = 0

Apabila sin θ = 0
θ = 0, π, 2π

Apabila 2 kos θ – 1= 0
kos θ = ½

θ= 1 3 π,  5 3 π Oleh itu, θ=0,  1 3 π, π,  5 3 π, 2π.

Bab 16 Fungsi Trigonometri

Posted on by

5.8.1 Fungsi Trigonometri, SPM Praktis (Kertas 2)

Soalan 1:
(a) Lakar graf y = kos 2x untuk 0o ≤ x ≤ 180o.
(b) Seterusnya, dengan menggunakan paksi yang sama, lakar satu garis lurus yang sesuai untuk mencari bilangan penyelesaian bagi persamaan 2  sin 2 x=2− x 180 untuk 0o ≤ x ≤ 180o.
Nyatakan bilangan penyelesaian itu.

Penyelesaian:
(a)(b)


(b)
2  sin 2 x=2− x 180 1−2  sin 2 x=1−( 2− x 180 ) kos2x= x 180 −1 y= x 180 −1

x = 0, y = –1
x = 180, y = 0
Bilangan penyelesaian = 2



Soalan 2:
(a) Lakar graf y= 3 2 kos2x untuk 0≤x≤ 3 2 π.  
(b) Seterusnya, dengan menggunakan paksi yang sama, lakar satu garis lurus yang sesuai untuk mencari bilangan penyelesaian bagi persamaan 4 3π x−kos2x= 3 2  untuk 0≤x≤ 3 2 π  
Nyatakan bilangan penyelesaian itu.

Penyelesaian:
(a)(b)



(b)
4 3π x−kos2x= 3 2 kos2x= 4 3π x− 3 2 3 2 kos2x= 3 2 ( 4 3π x− 3 2 ) y= 2 π x− 9 4 Untuk melakar graf y= 2 π x− 9 4 x=0, y=− 9 4 x= 3π 2 , y= 3 4
Bilangan penyelesaian
= bilangan titik persilangan
= 3

Bab 16 Fungsi Trigonometri

Posted on by

5.2.2 Sudut Khas
 
1. Nilai fungsi trigonometri bagi sudut-sudut khas
(a) Nilai bagi sudut khas 30odan 60o

 
  (a)sin 30 o = 1 2  (b)kos 30 o = 3 2 (c)tan 30 o = 1 3   (d)sin 60 o = 3 2   (e)kos 60 o = 1 2    (f)tan 60 o = 3    
(b)  Nilai bagi sudut khas 45o

    (a)sin 45 o = 1 2   (b)kos 45 o = 1 2   (c)tan 45 o =1   

(c)  Nilai bagi sudut khas 0o, 90o, 180o ,270o ,360o
(i) Graf y = sin x, 0o ≤ x ≤ 360o


  
x
0o
90o
180o
270o
360o
sin
0
1
0
-1
0


(ii) Graf y = kos x, 0o ≤ x ≤ 360o





(iii) Graf y = tan x, 0o ≤ x ≤ 360o



x
0o
90o
180o
270o
360o
tan
0
∞
0
∞
0


Bab 16 Fungsi Trigonometri

Posted on by
5.7.6 Fungsi Trigonometri, SPM Praktis (Kertas 1)

Soalan 15:
Buktikan identiti 2 kos2A+1 =se k 2 A

Peneyelesaian:
Sebelah kiri =  2 kos2A+1 = 2 ( 2ko s 2 A−1 )+1 ← kos2A=2ko s 2 A−1 = 2 2ko s 2 A = 1 ko s 2 A =se k 2 A =Sebelah kanan


Soalan 16:
Buktikan identiti 2tanA 2−se k 2 A =tan2A

Peneyelesaian:
Sebelah kiri =  2tanA 2−se c 2 A = 2tanA 2−( tan 2 A+1 ) ← tan 2 A+1=se c 2 A = 2tanA 1− tan 2 A =tan2A =Sebelah kanan


Soalan 17:
Buktikan identiti tan x + kot x = 2 kosek 2x

Peneyelesaian:
Sebelah kiri,
tan x + kot x
= sin x k o s x + k o s x sin x = sin 2 x + k o s 2 x k o s x sin x = 1 k o s x sin x ← sin 2 x + k o s 2 x = 1 = 1 1 2 sin 2 x ← sin 2 x = 2 sin x k o s x 1 2 sin 2 x = sin x k o s x = 2 sin 2 x = 2 ( 1 sin 2 x ) = 2 k o s e k   2 x = Sebelah kanan


Soalan 18:
Buktikan identiti kosx−sin2x kos2x+sinx−1 = 1 tanx   

Peneyelesaian:
Sebelah kiri kosx−sin2x kos2x+sinx−1 = kosx−2sinxkosx ( 1−2 sin 2 x )+sinx−1 ← kos2x=1−2 sin 2 x = kosx( 1−2sinx ) sinx−2 sin 2 x = kosx( 1−2sinx ) sinx( 1−2sinx ) = kosx sinx =kotx = 1 tanx Sebelah kanan

Bab 16 Fungsi Trigonometri

Posted on by
5.7.5 Fungsi Trigonometri, SPM Praktis (Kertas 1)

Soalan 11:
Buktikan identiti ko s 2 x 1−sinx =1+sinx 

Peneyelesaian:
Sebelah kiri = ko s 2 x 1−sinx = 1− sin 2 x 1−sinx ← sin 2 x+ko s 2 x=1 = ( 1+sinx )( 1−sinx ) 1−sinx =1+sinx = Sebelah kanan  


Soalan 12:
Buktikan identiti sin 2 x−ko s 2 x= tan 2 x−1 tan 2 x+1   

Peneyelesaian:
Sebelah kanan  tan 2 x−1 tan 2 x+1 = sin 2 x cos 2 x −1 sin 2 x cos 2 x +1 ← tanx= sinx cosx = sin 2 x− cos 2 x cos 2 x sin 2 x+ cos 2 x cos 2 x = sin 2 x− cos 2 x sin 2 x+ cos 2 x = sin 2 x− cos 2 x← sin 2 x+ cos 2 x=1 =Sebelah kiri


Soalan 13:
Buktikan identiti tan2 θ – sin2 θ = tan2θ sin2 θ

Peneyelesaian:
Sebelah kiri = tan 2 θ− sin 2 θ = sin 2 θ cos 2 θ − sin 2 θ = sin 2 θ− sin 2 θ cos 2 θ cos 2 θ = sin 2 θ( 1− cos 2 θ ) cos 2 θ = sin 2 θ sin 2 θ cos 2 θ =( sin 2 θ cos 2 θ )( sin 2 θ ) = tan 2 θ sin 2 θ =Sebelah kanan


Soalan 14:
Buktikan identiti kosek2 θ (sek2 θ – tan2 θ) – 1 = kot2 θ

Peneyelesaian:
Sebelah kiri,
kosek2 θ (sek2θ – tan2 θ) – 1
= kosek2 θ (1) – 1  ← (tan2 θ + 1 = sek2θ
                                    sek2 θ – tan2θ  = 1)
= kosek2 θ – 1
= kot2 θ  ←(1 + kot2 θ = kosek2 θ
                        kosek2 θ – 1 = kot2 θ  )
= Sebelah kanan

Bab 16 Fungsi Trigonometri

Posted on by

5.2.1 Enam Fungsi Trigonometri bagi Sebarang Sudut

(A) Mentakrifkan Sinus, kosinus, tan, kosek, sek and kot



1. Katakan P (x, y) ialah sebarang sudut yang terletak pada lilitan bulatan yang berpusat O dan berjejari, j. Berdasarkan ∆ OPQ dalam rajah di atas,

  • sinθ= y r • kosθ= x r • tanθ= y x   
 
2. Bagi sebarang sudut θ,

  • tanθ= sinθ kosθ   • kotθ= 1 tanθ = kosθ sinθ      • sekθ= 1 kosθ   • kosekθ= 1 sinθ
3. Hubungan antara nisbah trigonometri suatu sudut θdengan sudut pelengkapnya (90o – θ) adalah:


   
   Sudut Pelengkap:
   • sin θ = kos (90o – θ)   
   • kos θ = sin (90o – θ)   
   • tan θ = kot (90o – θ)   
   • kot θ = tan (90o – θ)   
   • sek θ = kosek (90o – θ)
   • kosek θ = sek (90o – θ)
  
Misalnya,
(a) sin 75o= kos (90o – 75o) = kos 15o
(b) tan 50o= kot (90o – 50o) = kot 20o
(c) sek 25o= kosek (90o – 25o) = kosek 65o


4. Hubungan nisbah trigonometri bagi sebarang sudut negative (–θ) adalah:

   
   Sudut Negatif:
   • sin (–θ) = –sin θ   
   • kos (–θ) = kos θ  
   • tan (–θ) = –tanθ
· Sudut negatif ialah sudut yang diukur mengikut arah jam dari arah positif paksi-x.
 · Misalnya, –60o adalah sepadan dengan 300o (360o – 60o).

Contoh:
Ungkapkan setiap fungsi trigonometri yang berikut dalam sebutan nisbah sudut tirus trigonometri.
Seterusnya, cari nilainya dengan menggunakan kalkulator.
(a) kos (– 325o)
(b) tan (– 124o)
(c) sin (– 115o)

Penyelesaian:
(a) kos (– 325o)
= kos 325o   ← {rumus kos (–θ) = kos θ digunakan}
= kos (360o– 325o) ← {kos bernilai positif di sukuan keempat}
= kos 35o
= 0.8192

(b) tan (– 124o)
= – tan 124o   ← {rumus tan (–θ) = – tan θ digunakan }
= – [– tan (180o– 124o)] ← {tan bernilai negatif di sukuan kedua}
= tan 56o
= 1.483

(c) sin (– 115o)
= – sin 115o   ← {rumus sin (–θ) = – sin θ digunakan }
= – sin (180o– 115o) ← {sin bernilai positif di sukuan kedua}
= – sin 65o
= – 0.9063

Bab 16 Fungsi Trigonometri

Posted on by

5.1 Sudut Positif dan Sudut Negatif dalam Darjah dan Radian

1. Sudut positif ialah sudut yang diukur mengikut arah lawan jam dari arah positif paksi-x.
2. Sudut negatif ialah sudut yang diukur mengikut arah jam dari arah positif paksi-x.
 

3. Satu putaran lengkap ialah 360°atau 2π radian.


Contoh:
Tunjukkan setiap sudut yang berikut dalam rajah yang berasingan dan nyatakan sukuan terletaknya sudut tersebut.
(a) 410°
(b) 890°
(c) 22 9 π radian
(d) 10 3 π radian
(e) –60o
(f) –500°
(g)−3 1 4 π radian


Penyelesaian:
(a)


410° = 360° + 50°
Maka, sudut 410° terletak pada sukuan pertama.


(b)


890° = 720° + 170°
Maka, sudut 170° terletak pada sukuan kedua.


(c)


22 9 π rad=( 2π+ 4 9 π ) rad= 360 o + 80 o
Maka, sudut 22 9 π radian  terletak pada sukuan pertama.


(d)


10 3 π rad=( 3π+ 1 3 π ) rad= 540 o + 60 o  
Maka, sudut 10 3 π radian  terletak pada sukuan ketiga.

(e)


Maka, sudut –60° terletak pada sukuan keempat.


(f)


–500° = –360° – 140°
Maka, sudut –500° terletak pada sukuan ketiga.

(g)


−3 1 4 π rad=( −3π− 1 4 π ) rad=− 540 o − 45 o  

Maka, sudut −3 1 4 π radian terletak pada sukuan kedua.

Bab 16 Fungsi Trigonometri

Posted on by

5.7.3 Fungsi Trigonometri, SPM Praktis (Kertas 1)
Soalan 7:
Diberi bahawa sinA= 5 13  dan kosB= 4 5 , dengan keadaan A ialah sudut cakah dan B ialah
sudut tirus. Cari
(a) tan A
(b) sin (A + B)
(c) kos (A – B)

Penyelesaian:

(a)
tan A = − 5 12

(b)
sin ( A + B ) = sin A k o s B + k o s A sin B sin ( A + B ) = ( 5 13 ) ( 4 5 ) + ( − 12 13 ) ( 3 5 ) ← k o s A = − 12 13 sin B = 3 5 = 4 13 − 36 65 = − 16 65

(c)
k o s ( A − B ) = k o s A k o s B + sin A sin B k o s ( A − B ) = ( − 12 13 ) ( 4 5 ) + ( 5 13 ) ( 3 5 ) k o s ( A − B ) = − 33 65


Soalan 8:
Jika sin A = p, dan 90° < A < 180°, ungkap dalam sebutan p
(a) tan A
(b) cos A
(c) sin 2A

Penyelesaian:


Guna Teori Pythagoras, Sisi bersebelahan = 1 2 − p 2 = 1 − p 2

(a)
tan A = − p 1 − p 2 ← tan bernilai negatif di sukuan II

(b)
kosA=− 1− p 2 ← kos bernilai negatif di sukuan II sinA=2sinAkosA sinA=2( p )( − 1− p 2 ) sinA=−2p 1− p 2

(c)
sin A = 2 sin A k o s A sin A = 2 ( p ) ( − 1 − p 2 ) sin A = − 2 p 1 − p 2


Bab 16 Fungsi Trigonometri

Posted on by
5.7.2 Fungsi Trigonometri, SPM Praktis (Kertas 1)

Soalan 5:
Cari semua sudut antara 0° dengan 360 ° yang memuaskan persamaan yang berikut:
(a)    2 sin ( 2x – 50o) = –1
(b)   15 sin2 x = sin x + 4 sin 30o
(c)    7 sin x kos x = 1  

Peneyelesaian:
(a)
2 sin ( 2x – 50o) = –1 
sin ( 2x – 50o) = –  ½
sudut asas ( 2x – 50o) = –30o   ← (sin adalah negatif di sukuan III dan IV)
2x – 50o = –30o, 180o + 30o, 360o – 30o, 360o+ 180o + 30o 
← (sudut diambil dalam julat 0o ≤ x≤ 720o, dalam putaran lengkap) 
2x – 50o = –30o, 210o, 330o, 570o 
2x = 20o, 260o, 380o, 620o 
Oleh itu x= 10o, 130o , 190o, 310o

(b)
15 sin2x = sin x + 4 sin 30o
15 sin2x = sin x + 4 (½)  ← (sin 30o= ½)
15 sin2x = sin x + 2
15 sin2x – sin x – 2 = 0
(5 sin x – 2)(2 sin x + 1) = 0
sinx= 2 5      atau     sinx=− 1 3 Apabila sinx= 2 5          
sudut asas = 23º 35’
x = 23º 35’, 180º – 23º 35’
x = 23º 35’, 156º 25’

Apabila sin x = – ⅓   ← (sin adalah negatif di sukuan III dan IV)     
sudut asas = 19º 28’
x = 180º + 19º 28’, 360º – 19º 28’
x = 199º 28’, 340º 32’
Oleh itu x= 23º 35’, 156º 25’, 199º 28’, 340º 32’.

(c)
7 sin x kos x = 1  
sinx kos x= 1 7 2sinx kos x= 2 7 ←( ×2 untuk kedua-dua belah ) sin2x= 2 7  
sin 2x = 0.2857
sudut asas x = 16º 36’
2x = 16º 36’, 180º – 16º 36’, 360º + 16º 36’, 360º + 180º – 16º 36’
2x = 16º 36’, 163º 24’, 376º 36’, 523º 24’
Oleh itu x= 8º 18’, 81º 42’, 188º 18’, 261º 42’.


Soalan 6:
Selesaikan persamaan 4 sin (x – π) cos (x – π) = 1 untuk 0o ≤ x ≤ 360o.

Peneyelesaian:
4 sin (x – π) kos (x – π) = 1
2 [2 sin (x – π) kos (x – π)] = 1
2 sin (x – π) kos (x – π) = ½
sin 2(x – π) = ½ ← (sin 2x = 2 sinx kosx)
sin 2(x – 180o) = ½ ← (π rad = 180o)
sin (2x – 360o) = ½
sin 2x kos 360o – kos 2x sin 360o  =  ½
sin 2x (1) – kos 2x (0)  = ½ ← (kos 360o = 1, sin 360o= 0)
sin 2x = ½
sudut asas x = 30o ← (sudut khusus, sin 30o = ½)
2x = 30o, 150o, 390o, 510o
x = 15o, 75o, 195o, 255o

Bab 16 Fungsi Trigonometri

Posted on by

5.7.4 Fungsi Trigonometri, SPM Praktis (Kertas 1)

Soalan 9:
Given that sin θ = 3 5 , dengan keadaan θ ialah sudut tirus, tanpa menggunakan jadual atau kalkulator, cari nilai bagi
(a) sin (180º + θ),
(b) kos (180º – θ),
(c) tan (360º + θ).

Penyelesaian:


sinθ= 3 5          kosθ= 4 5         tanθ= 3 4

(a)
sin (180º + θ)
= sin 180º kos θ + kos 180º sin θ
= (0) kos θ + (– 1) sin θ
= – sin θ
= − 3 5

(b)
kos (180º – θ)
= kos 180º kos θ + sin 180º sin θ
= (– 1) kos θ + (0) sin θ
= – kos θ
= − 4 5

(c)
tan ( 360 ∘ + θ ) = tan 360 ∘ + tan θ 1 − tan 360 ∘ tan θ = 0 + tan θ 1 − ( 0 ) ( tan θ ) = tan θ = 3 4



Soalan 10:
Buktikan setiap identiti trigonometri yang berikut.
(a) kot2 x – kot2 x kos2x = kos2 x
(b) sek x sek x − k o s x = k o s e k 2 x

Penyelesaian:
(a)
Sebelah kiri:
kot2 x– kot2 x kos2 x
= kot2 x (1 – kos2 x)
= kot2 x (sin2 x)
= k o s 2 x s i n 2 x ( s i n 2 x ) = k o s 2 x (Sebelah kanan)

(b)
Sebelah kiri: sek x sek x − k o s x = 1 k o s x 1 k o s x − k o s x = 1 k o s x 1 k o s x − k o s 2 x k o s x = 1 k o s x 1 − k o s 2 x k o s x = 1 k o s x × k o s x 1 − k o s 2 x = 1 1 − k o s 2 x = 1 s i n 2 x = k o s e k 2 x (Sebelah kanan)