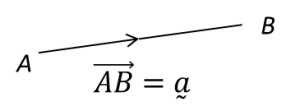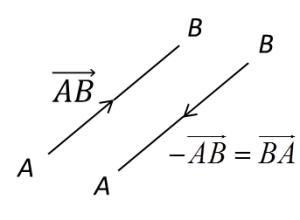4.5 Vektor dalam Satah Cartes
1.
Vektor unit mempunyai magnitud satu unit.
2.
Vektor ialah vektor unit ke arah positif paksi-x.
Vektor ialah vektor unit ke arah positif paksi-y.
3.
Suatu vektor dalam satah Cartes boleh ditulis dalam bentuk
4.
Magnitud bagi vektor unit ialah
5. Magnitud bagi vektor Contoh 1:
Jika cari nilai k. Tentukan vektor unit dalam arah bagi setiap nilai k.
Penyelesaian:
Contoh 2:
Diberi bahawa
(a) Cari
(b) Seterusnya, cari vektor unit dalam arah
Penyelesaian:
(a)
(b)