Bab 2 Persamaan Kuadratik

Posted on September 29, 2016 by user

2.6 Persamaan Kuadratik, SPM Praktis (Kertas 2)

Soalan 2:

Diberi α dan β ialah punca-punca bagi persamaan kuadratik (2x + 5)(x + 1) + p = 0 dengan keadaan αβ = 3 dan p ialah pemalar.

Cari nilai p, α dan β.

Penyelesaian:

(2x + 5)(x + 1) + p = 0

2x² + 2x + 5x + 5 + p = 0

2x² + 7x + 5 + p = 0

*Bandingkan dengan, x² – (hasil tambah dua punca)x + hasil darab dua punca = 0

x^{2} + \frac{7}{2} x + \frac{5 + p}{2} = 0 \leftarrow \begin{array}{l} bahagi kedua-dua \\ belah dengan 2 \end{array}

Hasil darab dua punca, αβ = 3

\frac{5 + p}{2} = 3

5 + p = 6

p = 1

Hasil tambah dua punca =

- \frac{7}{2}

\begin{array}{l} α + β = - \frac{7}{2} \to (1) \\ dan α β = 3 \to (2) \\ daripada (2), β = \frac{3}{α} \to (3) \\ Gantikan (3) ke dalam (1), \\ α + \frac{3}{α} = - \frac{7}{2} \end{array}

2α²+ 6 = –7α ← (darab kedua-dua belah dengan 2α)

2α²+ 7α + 6 = 0

(2α + 3)(α + 2) = 0

2α + 3 = 0 atau α + 2 = 0

α = - \frac{3}{2}

α = –2

\begin{array}{l} Gantikan α = - \frac{3}{2} dalam (3), \\ β = \frac{3}{- \frac{3}{2}} = 3 (- \frac{2}{3}) = - 2 \end{array}

Gantikan α = –2 dalam (3),

\begin{array}{l} β = - \frac{3}{2} \\ Oleh itu, p = 1, dan \\ apabila α = - \frac{3}{2}, β = - 2 dan α = - 2, β = - \frac{3}{2} . \end{array}

Bab 5 Indeks dan Logaritma

Posted on September 28, 2016 by user

5.6 Indeks dan Logaritma, SPM Praktis (Soalan Panjang)

Soalan 1

(a) Cari nilai bagi

i. 2 log₂ 12 + 3 log₂5 – log₂ 15 – log₂ 150.

ii. log₈32

(b) Tunjukkan bahawa 5ⁿ + 5ⁿ ⁺ ¹+ 5ⁿ ⁺ ² boleh dibahagi dengan 31 bagi semua nilai nyang merupakan integer positif.

Penyelesaian:

(a)(i)

2 log₂ 12 + 3 log₂ 5 – log₂15 – log₂ 150

= log₂ 12² + log₂ 5³– log₂ 15 – log₂ 150

= \log_{2} \frac{12^{2} \times 5^{3}}{15 \times 150}

= log₂ 8

= log₂ 2³

= 3

(a)(ii)

\begin{array}{l} \log_{8} 32 = \frac{\log_{2} 32}{\log_{2} 8} \\ = \frac{\log_{2} 2^{5}}{\log_{2} 2^{3}} = \frac{5}{3} \end{array}

(b)

5ⁿ + 5ⁿ ⁺ ¹ + 5ⁿ ⁺ ²

= 5ⁿ + (5 × 5ⁿ ) + (5² × 5ⁿ )

= 5ⁿ (1 + 5 + 5²)

= 31 × 5ⁿ

Oleh itu, 5ⁿ + 5ⁿ ⁺ ¹ + 5ⁿ ⁺ ² boleh dibahagi dengan 31 bagi semua nilai nyang merupakan integer positif.

Soalan 2:

(a) Diberi log₁₀ x = 3 dan log₁₀y = –2. Tunjukkan bahawa 2xy – 10000y² = 19.

(b) Selesaikan persamaan log₃ x = log₉(x + 6).

Penyelesaian:

(a)

log₁₀x = 3 → (x = 10³)

log₁₀y = –2 → (y = 10^-2)

2xy – 10000y² = 19

Sebelah kiri:

2xy – 10000y²

= 2 × 10³× 10^-2– 10000 (10^-2)²

= 20 – 10000 (10^-4)

= 20 – 1

= 19

= sebelah kanan

(b)

\begin{array}{l} \log_{3} x = \log_{9} (x + 6) \\ \log_{3} x = \frac{\log_{3} (x + 6)}{\log_{3} 9} \\ \log_{3} x = \frac{\log_{3} (x + 6)}{\log_{3} 3^{2}} \\ \log_{3} x = \frac{\log_{3} (x + 6)}{2} \end{array}

2log₃ x= log₃ (x + 6)

log₃ x²= log₃ (x + 6)

x² = x + 6

x² – x – 6 = 0

(x + 2) (x – 3) = 0

x = – 2 atau 3.

log₃(– 2) tidak wujud.

Jadi, x = 3.

Bab 3 Fungsi Kuadratik

Posted on September 28, 2016 by user

3.7 Fungsi Kuadratik, SPM Praktis (Soalan Panjang)

Soalan 1:

Tanpa menggunakan kaedah pembezaan atau melukis graf, cari nilai maksimum atau nilai minimum bagi fungsi y = 2 + 4x – 3x². Seterusnya, cari persamaan paksi simetri bagi graf fungsi itu.

Penyelesaian:

Menyempurnakan kuasa dua bagi fungsi y dalam bentuk y = a(x+ p)² + q untuk mencari nilai maksimum atau nilai minimum bagi fungsi y.

y = 2 + 4x – 3x²

y = – 3x²+ 4x + 2 ← (Tulis dalam bentuk am)

\begin{array}{l} y = - 3 [x^{2} - \frac{4}{3} x - \frac{2}{3}] \\ y = - 3 [x^{2} - \frac{4}{3} x + {(- \frac{4}{3} \times \frac{1}{2})}^{2} - {(- \frac{4}{3} \times \frac{1}{2})}^{2} - \frac{2}{3}] \\ y = - 3 [{(x - \frac{2}{3})}^{2} - {(- \frac{2}{3})}^{2} - \frac{2}{3}] \end{array}

\begin{array}{l} y = - 3 [{(x - \frac{2}{3})}^{2} - \frac{4}{9} - \frac{6}{9}] \\ y = - 3 [{(x - \frac{2}{3})}^{2} - \frac{10}{9}] \\ y = - 3 {(x - \frac{2}{3})}^{2} + \frac{10}{3} \leftarrow Bentuk a {(x + p)}^{2} + q \end{array}

Didapati a = –3 < 0,

maka fungsi y mempunyai nilai maksimum

\frac{10}{3} .

\begin{array}{l} x - \frac{2}{3} = 0 \\ x = \frac{2}{3} \end{array}

Persamaan paksi simetri bagi graf fungsi itu ialah

x = \frac{2}{3} .

Soalan 2:
Fungsi kuadratik f(x) = x² – 4px + 5p² + 1 mempunyai nilai minimum m² + 2p, dengan keadaan m dan p adalah pemalar.
(a) Dengan menggunakan kaedah menyempurnakan kuasa dua, tunjukkan bahawa m = p – 1.
(b) Seterusnya, atau dengan cara lain, carikan nilai p dan nilai m jika graf bagi fungsi itu bersimetri pada x = m² – 1.

Penyelesaian:
(a)

\begin{array}{l} f (x) = x^{2} - 4 p x + 5 p^{2} + 1 \\ = x^{2} - 4 p x + {(\frac{- 4 p}{2})}^{2} - {(\frac{- 4 p}{2})}^{2} + 5 p^{2} + 1 \\ = {(x - 2 p)}^{2} + p^{2} + 1 \\ Nilai minimum, \\ m^{2} + 2 p = p^{2} + 1 \\ m^{2} = p^{2} - 2 p + 1 \\ m^{2} = {(p - 1)}^{2} \\ m = p - 1 \end{array}

(b)

\begin{array}{l} x = m^{2} - 1 \\ 2 p = m^{2} - 1 \\ p = \frac{m^{2} - 1}{2} \\ Diberi m = p - 1 \Rightarrow p = m + 1 \\ m + 1 = \frac{m^{2} - 1}{2} \\ 2 m + 2 = m^{2} - 1 \\ m^{2} - 2 m - 3 = 0 \\ (m - 3) (m + 1) = 0 \\ m = 3 atau - 1 \\ Apabila m = 3, \\ p = \frac{3^{2} - 1}{2} = 4 \end{array}

Bab 2 Persamaan Kuadratik

Posted on September 28, 2016 by user

2.6 Persamaan Kuadratik, SPM Praktis (Kertas 2)

Soalan 1:

(a) Cari nilai-nilai k supaya persamaan (1 – k) x²– 2(k + 5)x + k + 4 = 0 mempunyai punca yang sama.

Seterusnya, cari punca persamaan itu berdasarkan nilai-nilai k yang diperoleh.

(b) Diberi lengkung y = 5 + 4x – x²mempunyai persamaan tangen dalam bentuk y = px + 9. Hitung nilai-nilai p yang mungkin.

Penyelesaian:

(a)

Bagi punca-punca yang sama,

b²– 4ac = 0

[–2(k + 5)]² – 4(1 – k)( k + 4) = 0

4(k + 5)² – 4(1 – k)( k + 4) = 0

4(k² + 10k + 25) – 4(4 – 3k – k ² ) = 0

4k² + 40k + 100 – 16 + 12k + 4k²= 0

8k² + 52k + 84 = 0

2k² + 13k + 21 = 0

(2k + 7) (k + 3) = 0

k = - \frac{7}{2}, - 3

Jika

k = - \frac{7}{2}

, persamaan ialah

\begin{array}{l} (1 + \frac{7}{2}) x^{2} - 2 (- \frac{7}{2} + 5) x - \frac{7}{2} + 4 = 0 \\ \frac{9}{2} x^{2} - 3 x + \frac{1}{2} = 0 \end{array}

9x² – 6x + 1 = 0

(3x – 1) (3x – 1) = 0

x = ⅓

Jika k = –3, persamaan ialah

(1 + 3)x² – 2(–3 + 5)x – 3 + 4 = 0

4x² – 4x + 1 = 0

(2x – 1) (2x – 1) = 0

x = ½

(b)

y = 5 + 4x – x²----- (1)

y = px + 9 ---------- (2)

(1) = (2), 5 + 4x – x²= px + 9

x ² + px – 4x + 9 – 5 = 0

x ² + (p – 4)x + 4 = 0

Persamaan tangen mempunyai hanya satu titik persilangan, puncanya adalah sama.

b²– 4ac = 0

(p – 4)² – 4(1)(4) = 0

p ² – 8p + 16 – 16 = 0

p ² – 8p = 0

p (p – 8) = 0

Maka, p = 0 dan p = 8.

Bab 19 Taburan Kebarangkalian

Posted on September 27, 2016 by user

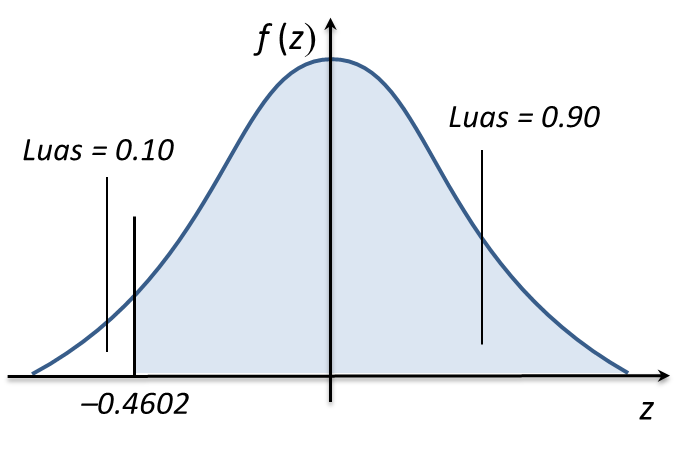
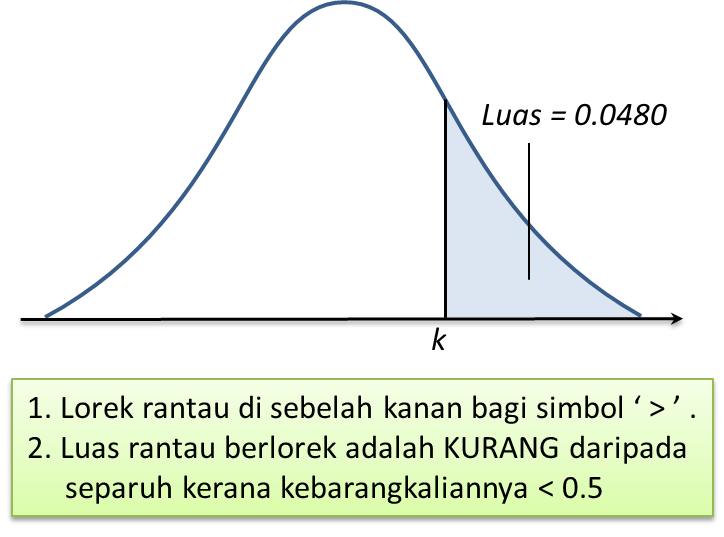
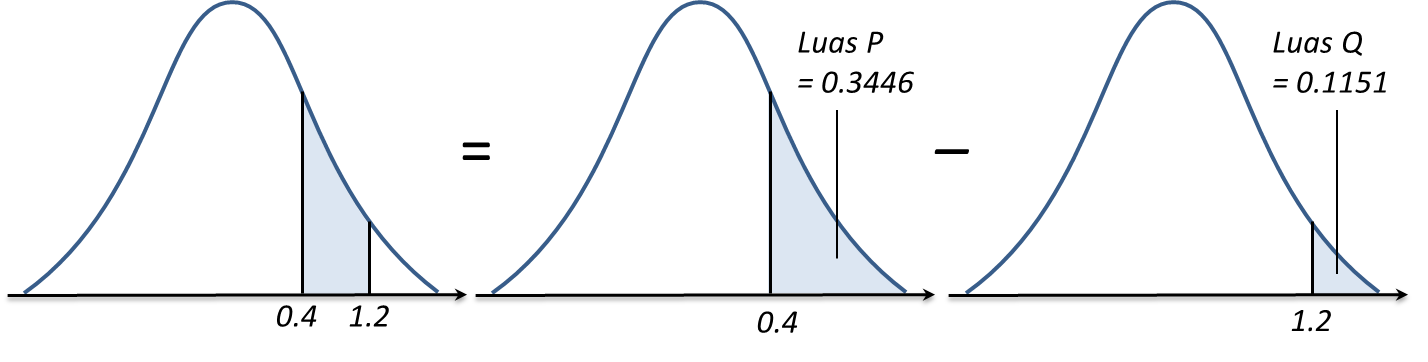
8.4 Taburan Kebarangkalian, SPM Praktis (Kertas 2)

Soalan 1:

Dalam suatu peperiksaan, 2 daripada 5 pelajar yang mengambil peperiksaan itu gagal dalam kertas kimia.

(a) Jika 6 orang dipilih secara rawak daripada pelajar-pelajar, cari kebarangkalian bahawa tidak melebihi 2 orang pelajar gagal dalam kertas kimia.

(b) Jika terdapat 200 orang pelajar tingkatan 4 dalam sekolah itu, cari min dan sisihan piawai bilangan orang pelajar gagal kertas kimia.

Penyelesaian:

(a)

X ~ Bilangan pelajar gagal kertas kimia

X ~ B (n, p)

X ~ B (6, \frac{2}{5})

P (X = r) = ⁿC_r. p^r. q^n-r

P (X ≤ 2)

= P(X = 0) + P(X = 1) + P(X= 2)

= C_{0} {(\frac{2}{5})}^{0} {(\frac{3}{5})}^{6} + C_{1} {(\frac{2}{5})}^{1} {(\frac{3}{5})}^{5} + C_{2} {(\frac{2}{5})}^{2} {(\frac{3}{5})}^{4}

= 0.0467 + 0.1866 + 0.3110

= 0.5443

(b)

X ~ B (n, p)

\begin{array}{l} X ~ B (200, \frac{2}{5}) \\ Min bagi X \\ = n p = 200 \times \frac{2}{5} = 80 \\ Sisihan piawai bagi X \\ = \sqrt{n p q} \\ = \sqrt{200 \times \frac{2}{5} \times \frac{3}{5}} \\ = \sqrt{48} \\ = 6.93 \end{array}

Soalan 2:

5% daripada bekalan mangga diterima oleh sebuah supermarket adalah rosak.

(a) Jika suatu sampel yang terdiri daripada 12 biji mangga dipilih secara rawak, cari kebarangkalian bahawa sekurang-kurangnya 2 biji mangga adalah rosak.

(b) Cari bilangan minimum mangga yang perlu dipilih supaya kebarangkalian untuk mendapatkan sekurang-kurangnya sebiji mangga rosak adalah lebih daripada 0.85.

Penyelesaian:

(a)

X ~ B (12, 0.05)

1 – P(X ≤ 1)

= 1 – [P(X = 0) + P (X = 1)]

= 1 – [¹²C₀ (0.05)⁰ (0.95)¹² + ¹²C₁ (0.05)¹ (0.95)¹¹]

= 1 – 0.8816

= 0.1184

(b)

P (X ≥ 1) > 0.85

1 – P(X = 0) > 0.85

P (X = 0) < 0.15

ⁿC₀(0.05)⁰ (0.95)ⁿ< 0.15

nlg 0.95 < lg 0.15

n > 36.98

n = 37

Oleh itu, bilangan minimum mangga yang perlu dipilih ialah 37 sekiranya kebarangkalian lebih daripada 0.85.

Soalan 3:

Dalam suatu kajian di sebuah sekolah, didapati bahawa 20% daripada pelajar tingkatan 5 gagal dalam peperiksaan tengah tahun. Jika 8 orang pelajar daripada sekolah itu dipilih secara rawak, cari kebarangkalian bahawa

(a) tepat 2 orang pelajar gagal dalam peperiksaan tengah tahun,

(b) kurang daripada 3 orang pelajar gagal dalam peperiksaan tengah tahun.

Penyelesaian:

(a)

p = 20% = 0.2,

q = 1 – 0.2 = 0.8

X ~ B (8, 0.2)

P (X = 2)

= ⁸C₂ (0.2)² (0.8)⁶

= 0.2936

(b)

P (X < 3)

= P(X = 0) + P (X = 1) + P (X = 2)

= ⁸C₀ (0.2)⁰ (0.8)⁸+ ⁸C₁ (0.2)¹ (0.8)⁷+ ⁸C₂ (0.2)²(0.8)⁶

= 0.16777 + 0.33554 + 0.29360

= 0.79691

Bab 19 Taburan Kebarangkalian

Posted on September 26, 2016 by user

8.2.3 Kebarangkalian Sesuatu Peristiwa

Contoh:

Jisim epal dalam sebuah gerai adalah bertaburan normal dengan min 220g dan varians 100g. Cari kebarangkalian bahawa sebiji epal dipilih secara rawak mempunyai jisim

(a) lebih daripada 230g.

(b) di antara 210g dengan 225g.

Seterusnya, cari nilai h supaya 90% daripada epal mempunyai jisim lebih daripada h g.

Penyelesaian:

μ = 220g

σ = √100 = 10g

Katakan X ialah jisim buah epal.

(a)

P (X > 230)

= P (Z > \frac{230 - 220}{10}) \leftarrow \begin{array}{l} Tukar kepada taburan normal \\ piawai ~ rumus Z = \frac{X - μ}{σ} \end{array}

= P (Z > 1)

= 0.1587

(b)

P (210 < X < 225)

= P (\frac{210 - 220}{10} < Z < \frac{225 - 220}{10}) \leftarrow \begin{array}{l} Tukar kepada taburan \\ normal piawai \end{array}

= P (–1 < Z < 0.5)

= 1 – P (Z > 1) – P (Z > 0.5)

= 1 – 0.1587 – 0.3085

= 0.5328

90% (kebarangkalian = 0.9) daripada epal mempunyai jisim lebih daripada h g,

P (X > h) = 0.9

P (X < h) = 1 – 0.9

= 0.1

Daripada sifir taburan normal piawai,

P (Z > 0.4602) = 0.1

P (Z < –0.4602) = 0.1

\frac{h - 220}{10} = - 0.4602

h – 220 = – 4.602

h = 215.4

Bab 19 Taburan Kebarangkalian

Posted on September 26, 2016 by user

8.2.2c Taburan Normal Piawai (Contoh 3)

Contoh 3:

Cari nilai bagi k jika

(a) P (Z > k) = 0.0480

(b) P (Z > k) = 0.8350

Penyelesaian:

(a)

Daripada sifir taburan normal piawai, k = 1.665

(b)

Daripada sifir taburan normal piawai,

k = –0.974 ← (nilai k adalah negatif kerana ia berada di sebelah kiri lengkung normal.

Bab 19 Taburan Kebarangkalian

Posted on September 26, 2016 by user

8.2.2b Taburan Normal Piawai (Contoh 2)

Contoh 2:

Cari nilai bagi setiap kebarangkalian yang berikut daripada sifir taburan normal piawai.

(a) P (0.4 < Z < 1.2)

(b) P (–1 < Z < 2.5)

Penyelesaian:

(a)

P (0.4 < Z < 1.2)

= Luas P – Luas Q

= Q (0.4) – Q (1.2) ← (bacaan daripada sifir taburan normal piawai bagi 0.4 dan 1.2 ialah 0.3446 dan 0.1151 masing-masing)

= 0.3446 – 0.1151

= 0.2295

(b)

P (–1 < Z < 2.5)

= 1 – Luas P – Luas Q

= 1 – Q (1) – Q (2.5)

= 1 – 0.1587 – 0.00621 ← (bacaan daripada sifir taburan normal piawai bagi 1 dan 2.5 ialah 0.1587 dan 0.00621 masing-masing)

= 0.8351

(c)

P (–1.3 < Z < –0.5)

= Luas P – Luas Q

= Q (0.5) – Q (1.3)

= 0.3085 – 0.0968 ← (bacaan daripada sifir taburan normal piawai bagi 0.5 dan 1.3 ialah 0.3085 dan 0.0968 masing-masing)

= 0.2117

Bab 19 Taburan Kebarangkalian

Posted on September 24, 2016 by user

8.2.2a Taburan Normal Piawai (Contoh 1)

Contoh 1:

Cari nilai bagi setiap kebarangkalian yang berikut daripada sifir taburan normal piawai.

(a) P (Z > 0.600)

(b) P (Z < –1.24)

(d) P (Z < 0.76)

Penyelesaian:

Sifir Taburan Normal Piawai

*Semasa membaca sifir taburan normal piawai, ia melibatkan penolakan nilai.

(a)

Daripada sifir taburan normal piawai, P (Z > 0.600) = 0.2743

(b)

P (Z < –1.24)

= P (Z > 1.24)

= Q (1.24)

= 0.1075 ← (Bacaan daripada sifir taburan normal piawai)

(*Dalam sifir taburan normal piawai, semua nilai bagi z adalah positif. Perhatikan bahawa lengkung itu adalah bersimetri pada paksi tegak, maka luas rantau berlorek bagi kedua-dua graf di atas adalah sama)

(c)

P (Z > –1.1)

= 1 – Luas P

= 1 – Q (–1.1)

= 1 – 0.1357 ← (Bacaan daripada sifir taburan normal piawai)

= 0.8643

(d)

P (Z < 0.76)

= 1 – Luas P

= 1 – Q (0.76)

= 1 – 0.2236 ← (Bacaan daripada sifir taburan normal piawai)

= 0.7764

Bab 19 Taburan Kebarangkalian

Posted on September 24, 2016 by user

8.2 Taburan Normal

(A) Pembolehubah Rawak Selanjar

1. Pembolehubah rawak selanjar ialah suatu pembolehubah yang boleh mengambil sebarang nilai di dalam suatu selang.

(B) Taburan Normal

1. Suatu pembolehubah rawak selanjar, X, adalah bertaburan normal jika grafnya meunjukkan ciri-ciri berikut.

(a) Lengkungnya berbentuk loceng

(b) Ia bersimetri pada paksi tegak yang melalui minnya, iaitu line x = μ.

(d) Luas rantau yang dibatasi oleh lengkung dan paksi-x ialah 1, iaitu jumlah kebarangkalian bagi semua nilai X ialah 1.

2. Pembolehubah rawak selanjar, X, yang bertaburan normal ditulis sebagai X ~ N (µ, σ²) dengan m ialah min dan σ² ialah varians.

(C) Taburan Normal Piawai

Jika suatu pembolehubah rawak normal, X, mempunyai min, µ = 0 dan sisihan piawai, σ = 1, maka X mengikut suatu taburan normal piawai, X ~ N (0, 1).

(D) Lengkung Suatu Taburan Normal Piawai

1. Lengkung bagi suatu taburan normal piawai mempunyai ciri-ciri yang berikut.

(a) Ia bersimetri pada paksi tegak yang melalui min, µ = 0 dan mempunyai varians, σ² = 1.

(b) Ia mempunyai nilai maksimum pada Z = 0.

(E) Penukaran Pembolehubah Suatu Taburan Normal kepada Pembolehubah Taburan Normal Piawai

1. Suatu taburan normal boleh ditukar kepada taburan normal piawai dengan menggunakan:

Z = \frac{x - μ}{σ}

dengan keadaan,

Z = skor piawai atau skor-z

X = nilai pembolehubah rawak normal

µ = min taburan normal

σ = sisihan piawai taburan normal