Question 10 (12 marks):
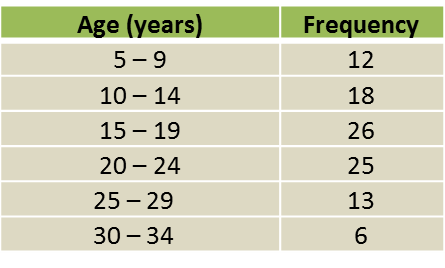
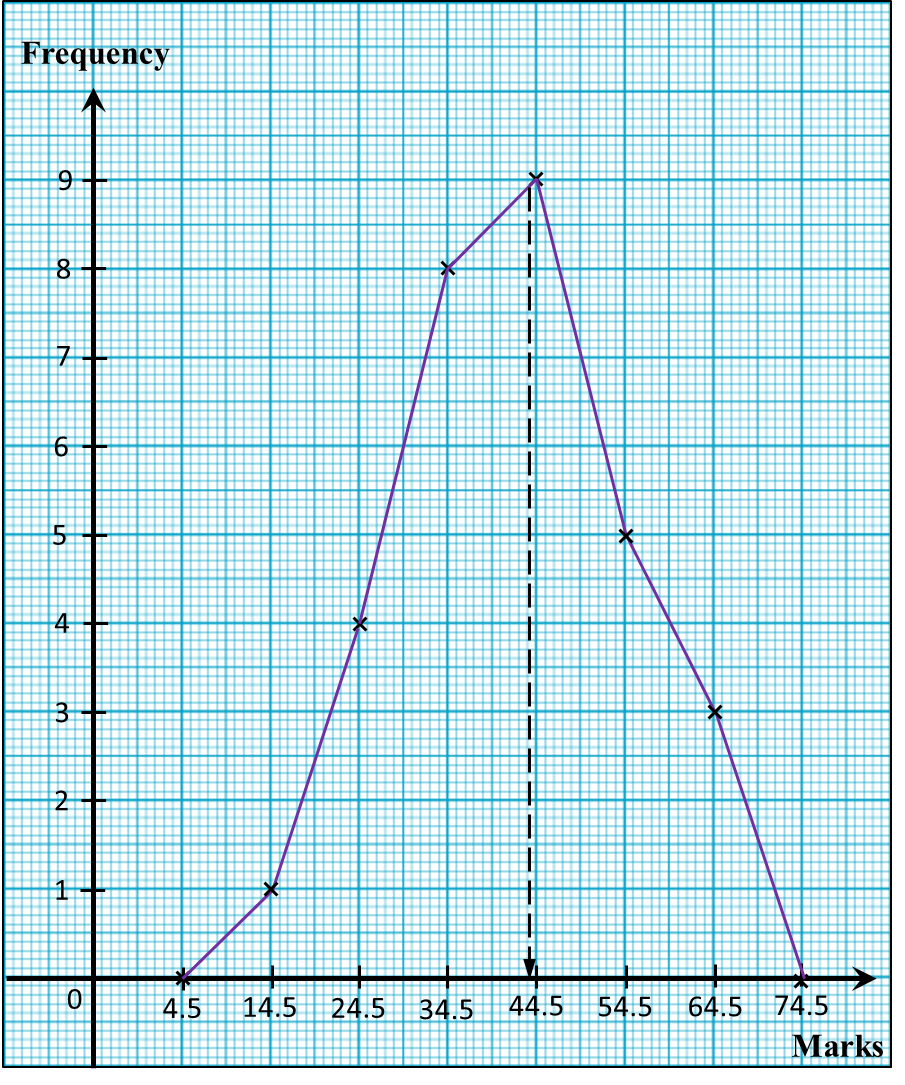
Diagram shows a histogram which represents the mass, in kg, for a group of 100 students.
 Diagram
Diagram
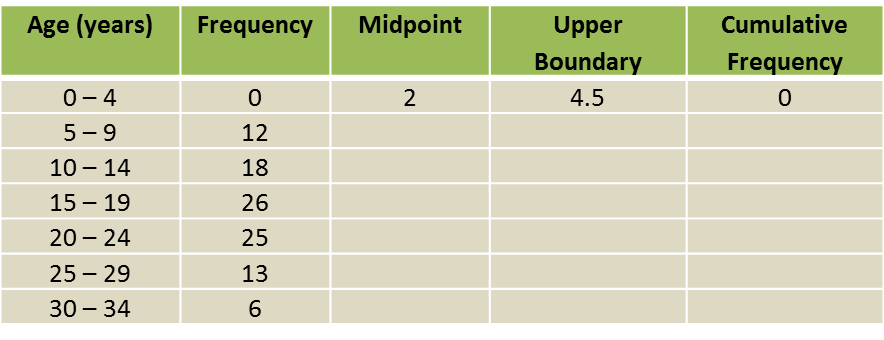
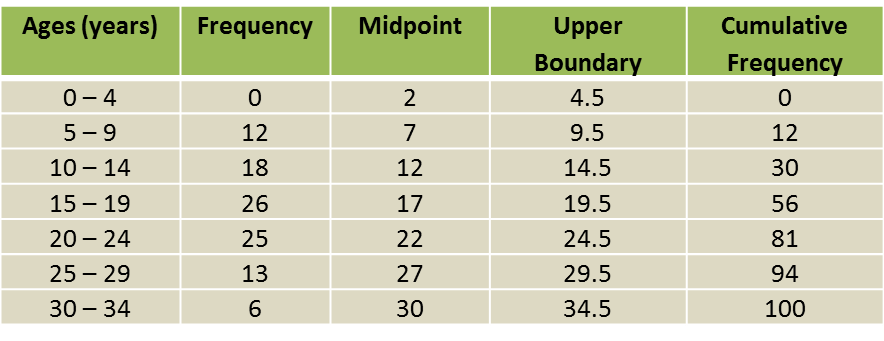
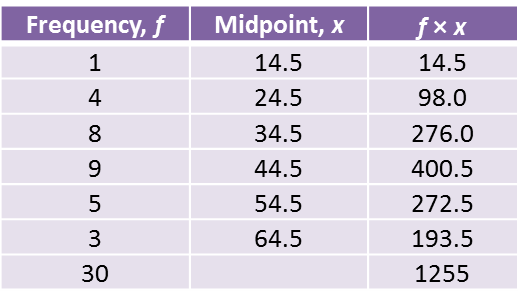
(a) Based on the Diagram, complete the Table in the answer space.
(b) Calculate the estimated mean mass of a student.
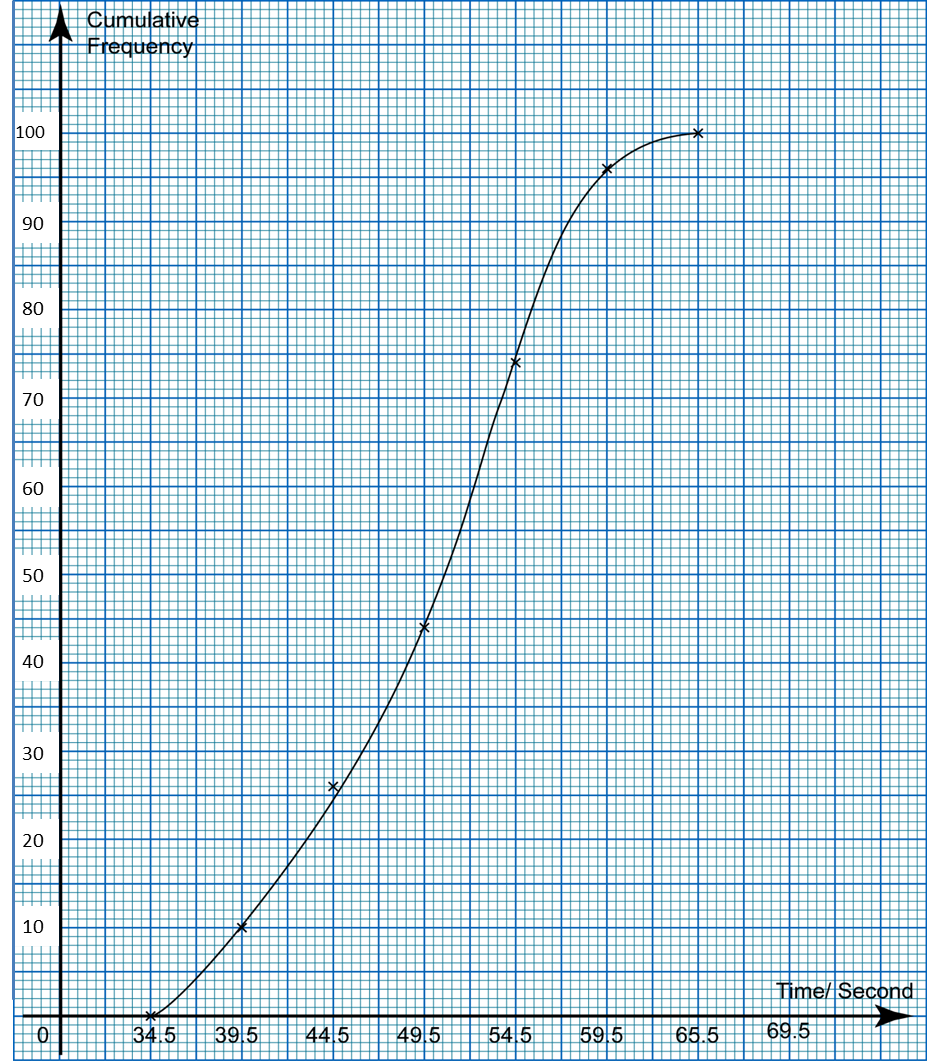
(c) For this part of the question, use graph paper. You may use a flexible curve ruler.
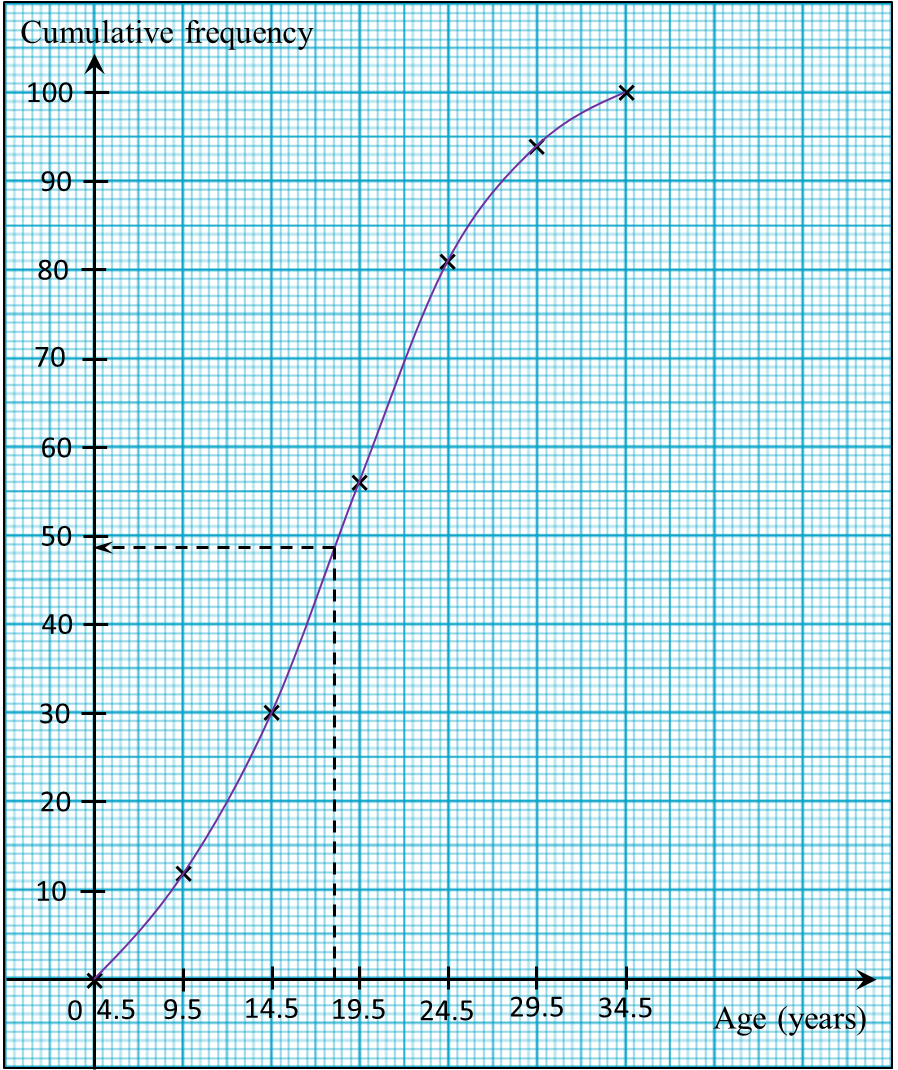
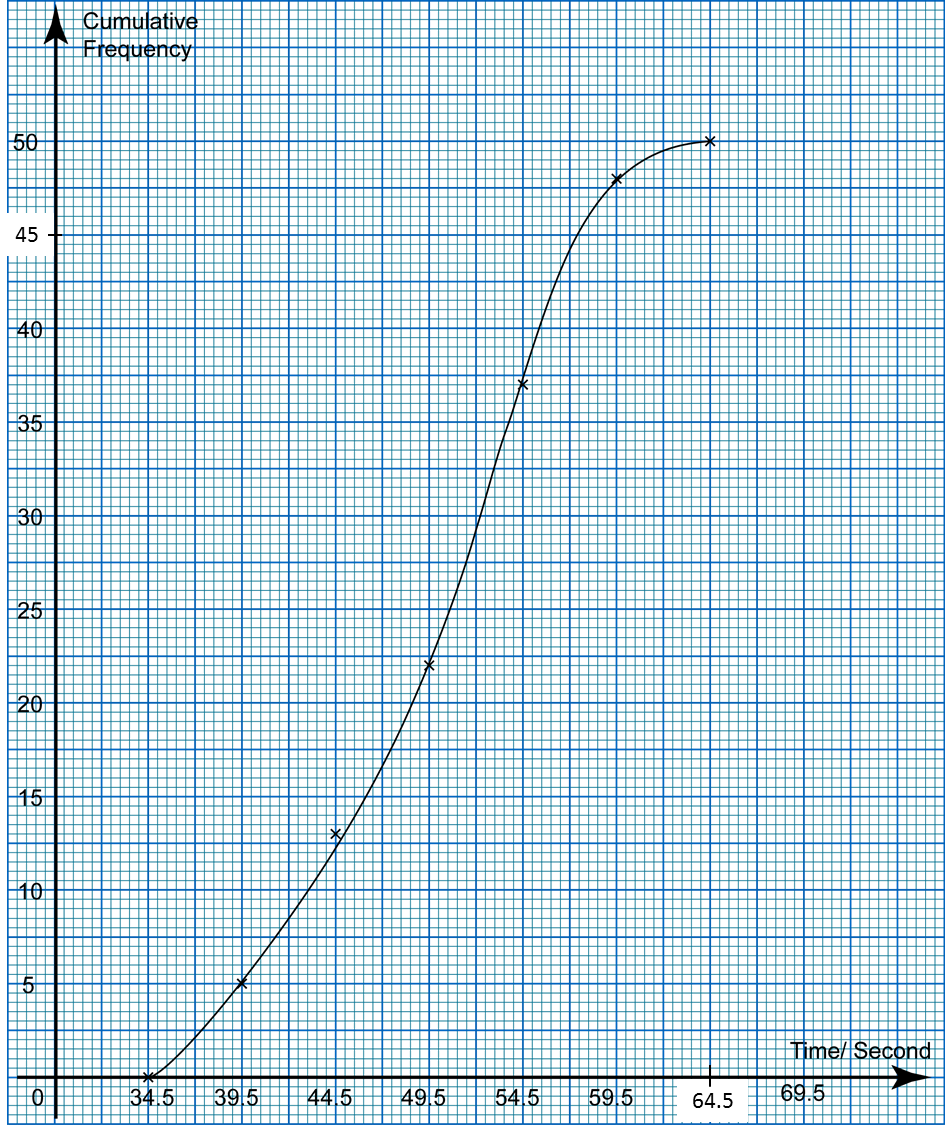
Using a scale of 2 cm to 10 kg on the horizontal axis and 2 cm to 10 students on the vertical axis, draw an ogive for the data.
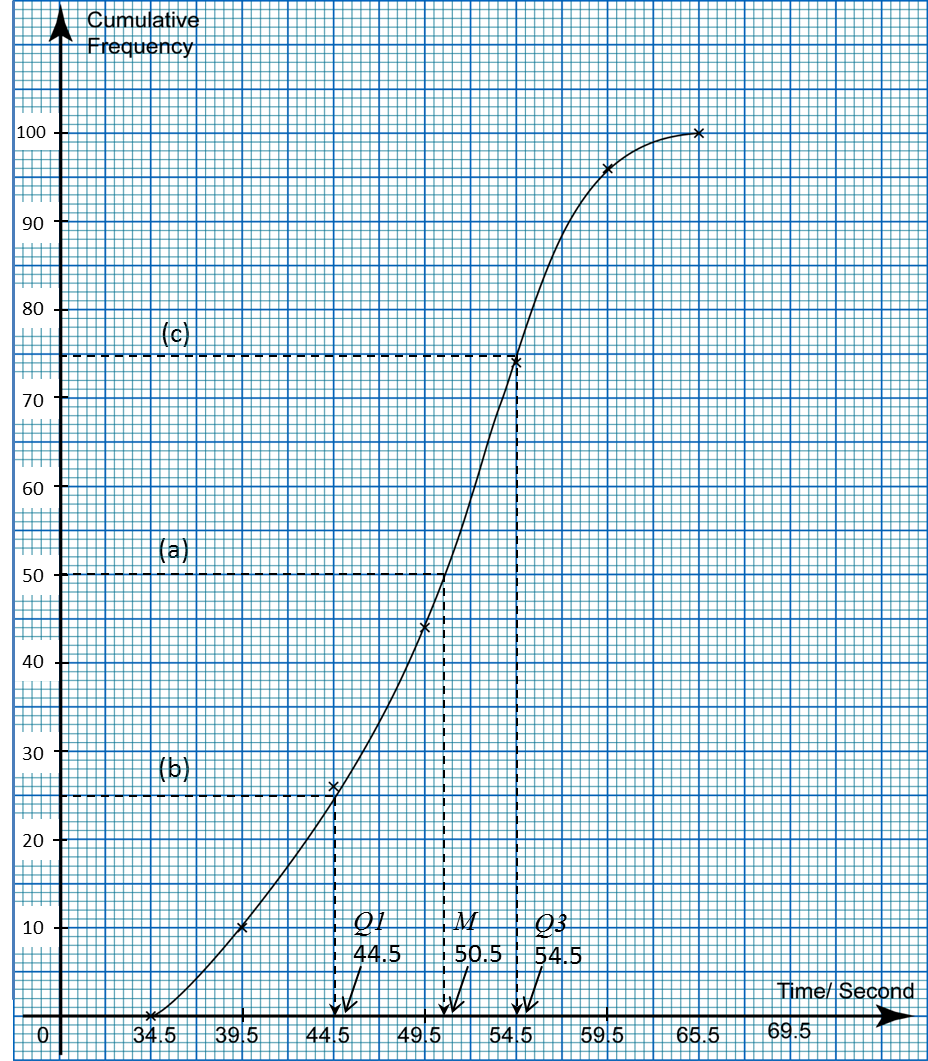
(d) Based on the ogive drawn in 10(c), state the third quartile.
Answer:

Solution:
(a)

(b)

(c)

(d)
Third quartile
= 75th student
= 90.0 kg
Diagram shows a histogram which represents the mass, in kg, for a group of 100 students.
 Diagram
Diagram(a) Based on the Diagram, complete the Table in the answer space.
(b) Calculate the estimated mean mass of a student.
(c) For this part of the question, use graph paper. You may use a flexible curve ruler.
Using a scale of 2 cm to 10 kg on the horizontal axis and 2 cm to 10 students on the vertical axis, draw an ogive for the data.
(d) Based on the ogive drawn in 10(c), state the third quartile.
Answer:

Solution:
(a)

(b)

(c)

(d)
Third quartile
= 75th student
= 90.0 kg
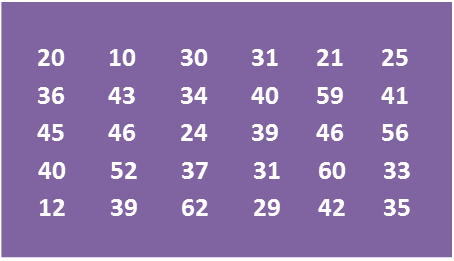 Diagram
Diagram


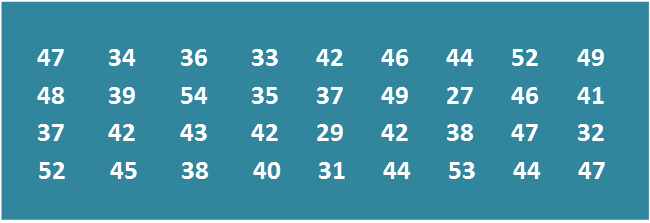 Diagram
Diagram Table
Table

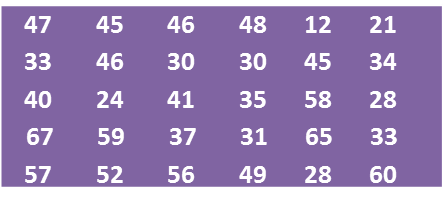
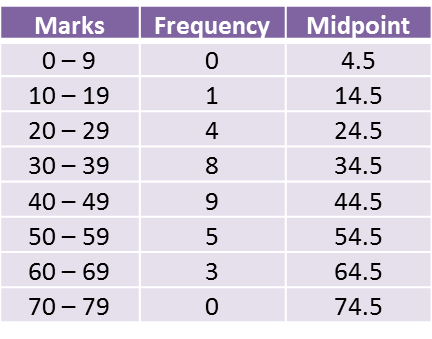
 (a) Using data in diagram above and a class interval of 5 marks, complete the table in the answer space.
(a) Using data in diagram above and a class interval of 5 marks, complete the table in the answer space.