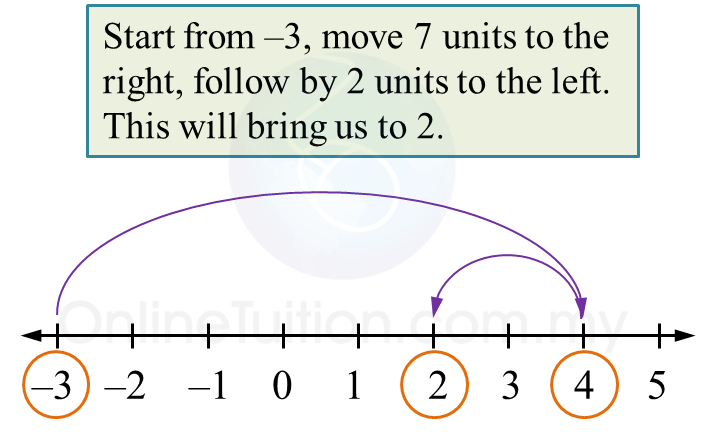
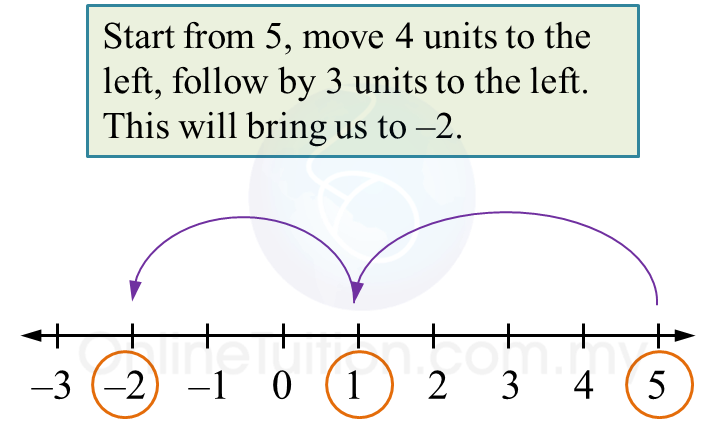
Question 6:
The mass of a box containing 6 papayas is 21.32 kg. The mass of the box when it is empty is 1.46 kg.
Calculate the average mass, in g, of a papaya.
Solution:
Mass of 6 papayas
= 21.32 – 1.46
= 19.86 kg
Average mass of a papaya
= 19.86 ÷ 6
= 3.31 kg
= 3.31 × 1000 g
= 3310 g
Question 7:
Louis bought 600 g of cookies. Dennis bought twice the mass of cookies that Jackson bought. They bought 1.35 kg of cookies altogether. Calculate the mass, in g, of cookies bought by Jackson.
Solution:
Let Jackson bought w g of cookies.
600 g + 2 × w + w = 1.35 kg
600 g + 3w = 1.35 kg
600 g + 3w = 1350 g
3w = 1350 g – 600 g
w = 750 g ÷ 3
w = 250 g
Question 8:
If the mass of 4 packets of candies is 2.6 kg, what is the mass of 9 packets of the same candies, in kg?
Solution:
Question 9:
It is given that
of fruits is supplied to Juice Stall A and
to Juice Stall B. The remaining 133.25 kg is sold to a fruit stall.
Calculate the mass of fruits that has been supplied to Fruit Stall B.
Solution:
Question 10:
The mixture of metal to produce a piece of 50 sen coin are
and the rest is copper.
If the mass of copper is 1.6 g, find the total mass, in g, of zinc and nickel.
Solution:

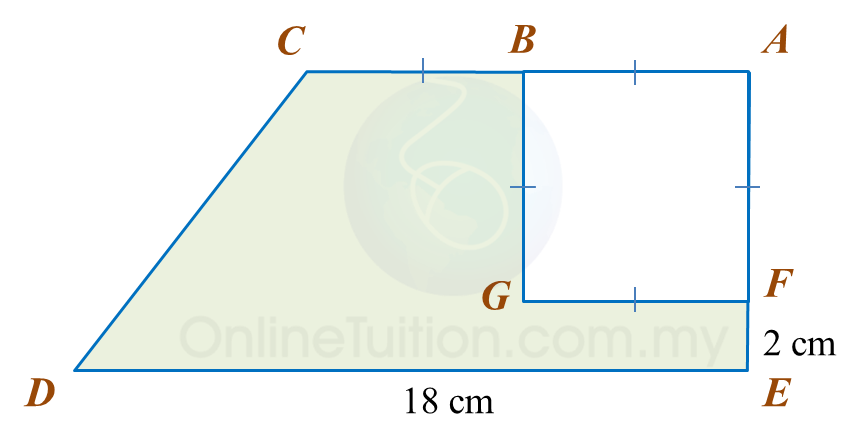
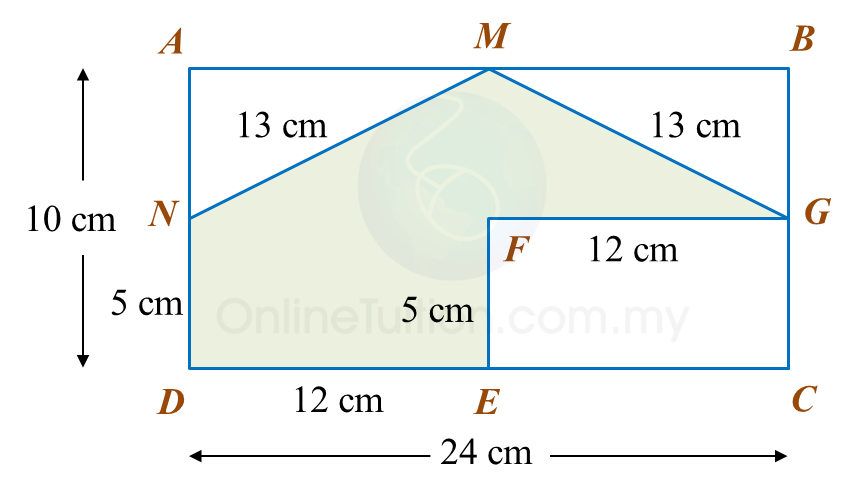
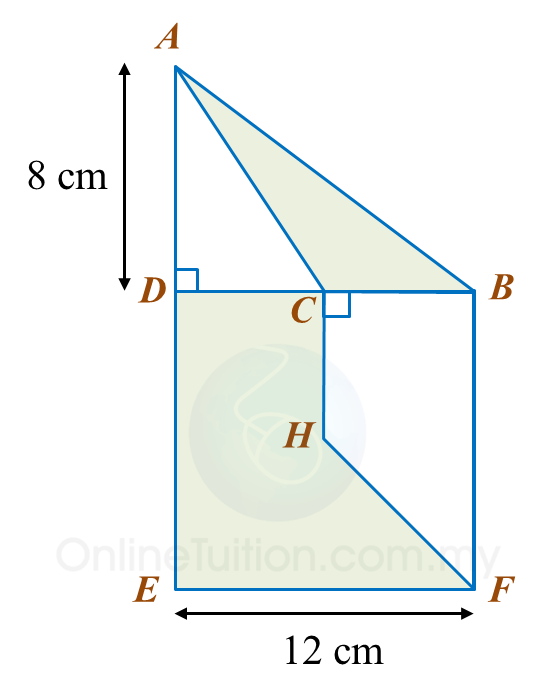 Calculate the area, in cm2, of the coloured region.
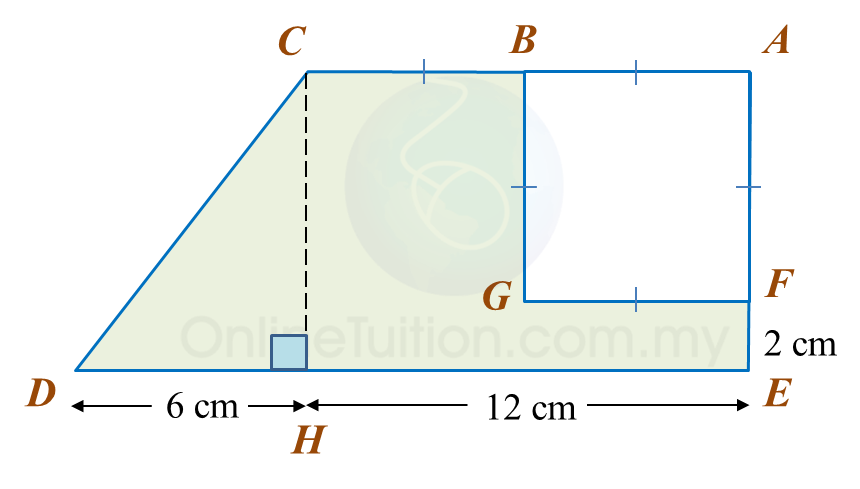
Calculate the area, in cm2, of the coloured region.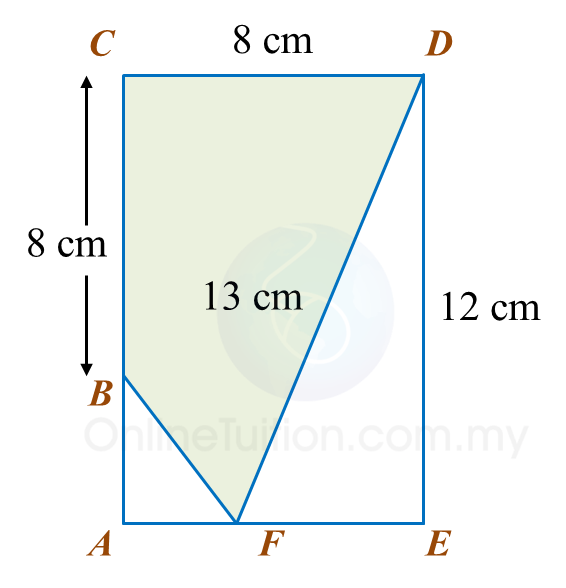
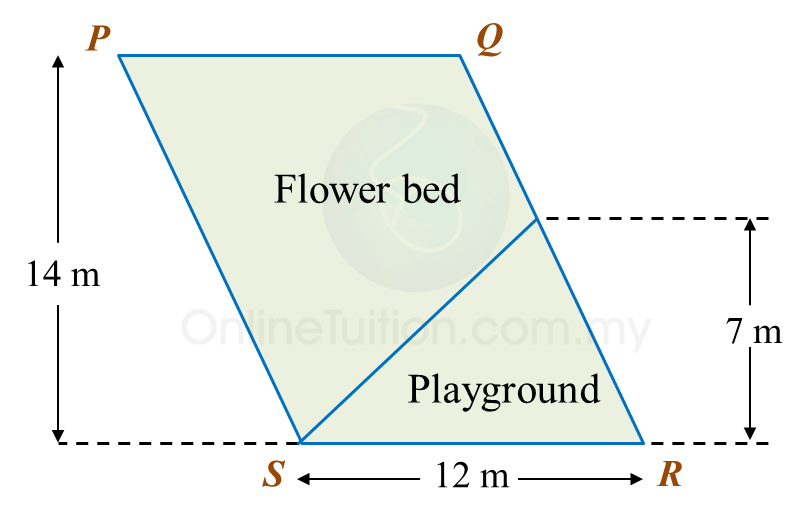 Calculate the area, in m2, of the flower beds.
Calculate the area, in m2, of the flower beds.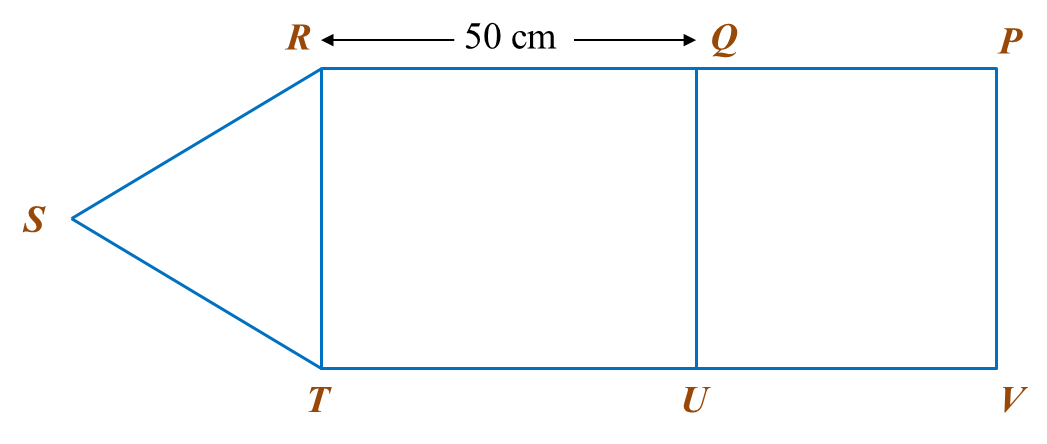
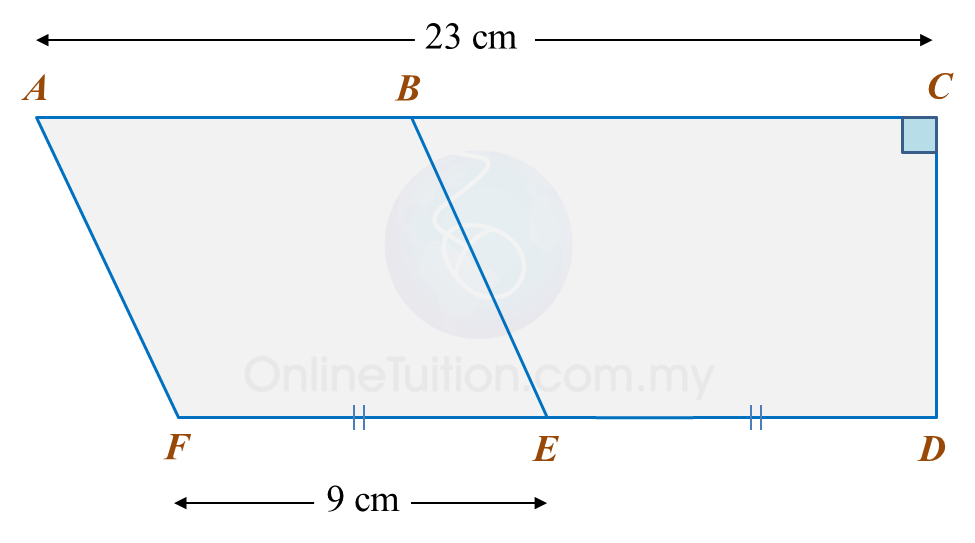 The area of ABEF is 72 cm2.
The area of ABEF is 72 cm2.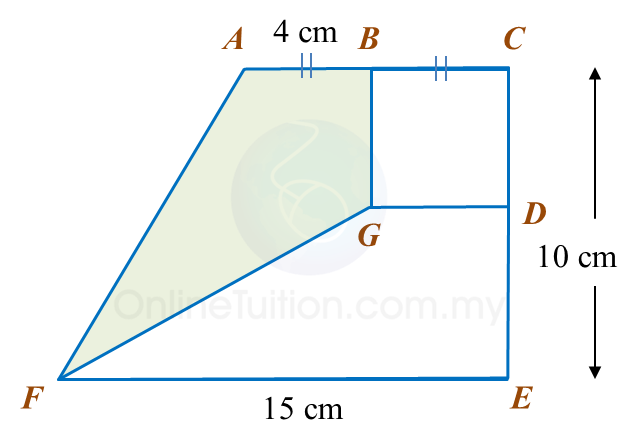
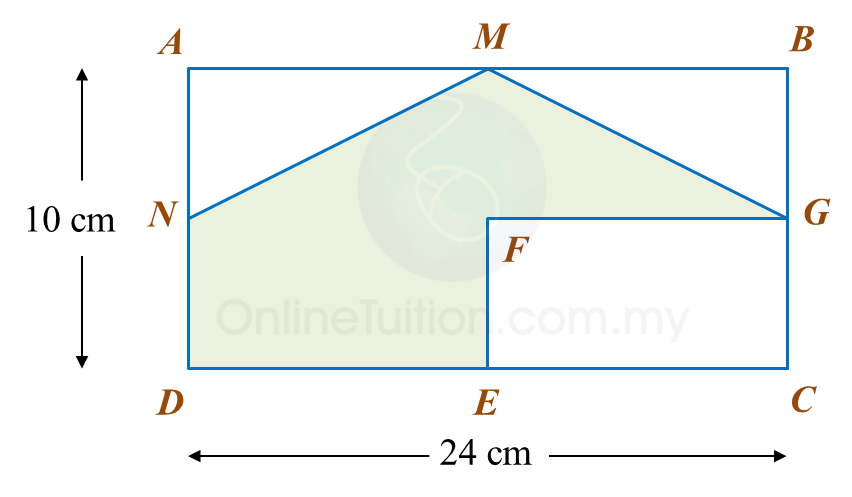
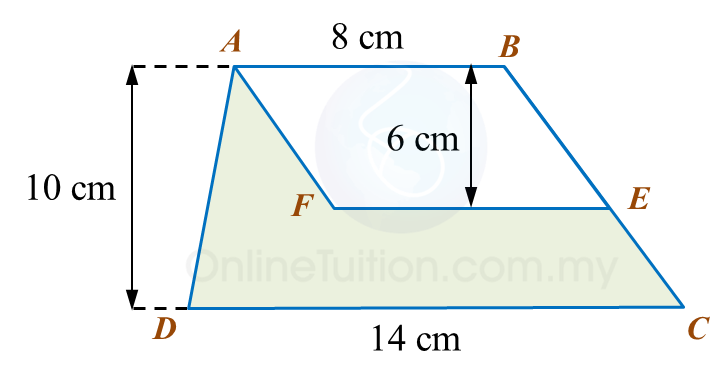 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.
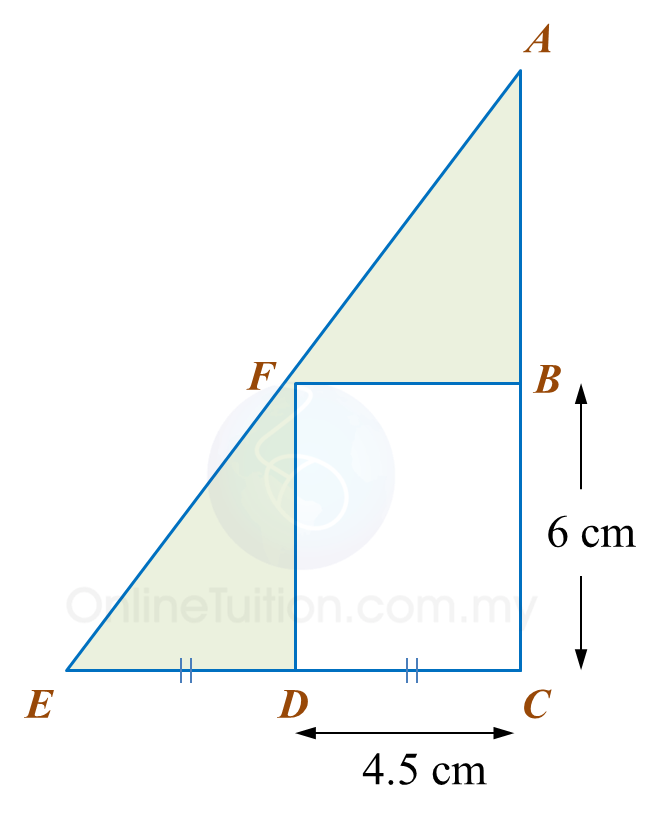 Calculate
Calculate