9.8 Pembezaan, SPM Praktis (Kertas 2)
Soalan 3:
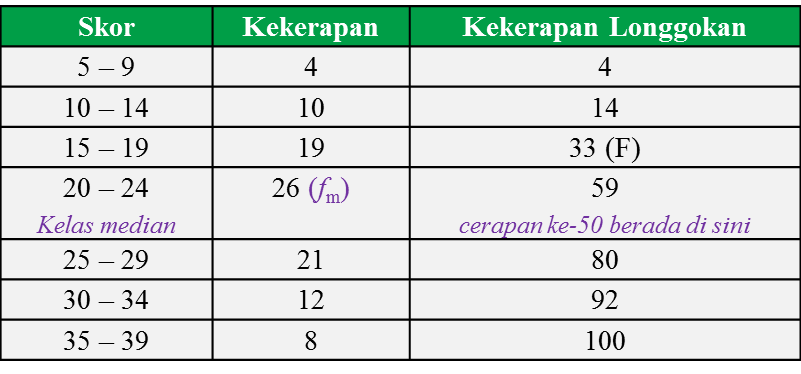
Lengkung y = x3 – 6x2 + 9x + 3 melalui titik P (2, 5) dan mempunyai dua titik pusingan A (3, 3) dan B.
Cari
(a) kecerunan lengkung itu pada P.
(b) persamaan normal kepada lengkung itu pada P.
(c) koordinat B dan menentukan sama ada B adalah titik maksimum atau titik minimum.
Penyelesaian:
(a)
y = x3 – 6x2 + 9x + 3
dy/dx = 3x2 – 12x + 9
di titik P (2, 5),
dy/dx = 3(2)2 – 12(2) + 9 = –3
Kecerunan lengung pada titik P = –3.
(b)
Kecerunan normal pada titik P = ⅓
persamaan normal pada P (2, 5):
y – y1 = m (x - x1)
y – 5 = ⅓ (x– 2)
3y – 15 = x – 2
3y = x + 13
(c)
Pada titik pusingan dy/dx= 0.
3x2 – 12x + 9 = 0
x2 – 4x + 3 = 0
(x – 1)( x – 3) = 0
x – 1 = 0 atau x – 3 = 0
x = 1 atau x = 3 (titik A)
Pada titik B:
x = 1
y = (1)3– 6(1)2 + 9(1) + 3 = 7
Maka, koordinat B = (1, 7)
Apabila x=1, d2ydx2=6x−12d2ydx2=6(1)−12d2ydx2=−6<0d2ydx2<0, B ialah titik maksimum.
Soalan 4:
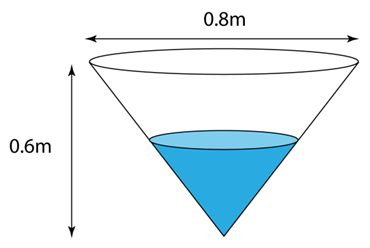
Rajah di atas menunjukkan sebuah kon dengan diameter 0.8m dan tinggi 0.6m. Air dituang ke dalam kon dengan kadar tetap 0.02m3s-1. Cari kadar perubahan tinggi paras air pada ketika tinggi parasnya ialah 0.5m.
Penyelesaian:
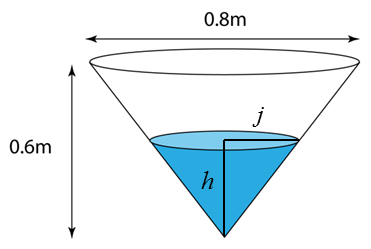
Isipadu air, I=13πj2hI=13π(23h)2hI=427πh3dIdh=(3)427πh2dIdh=49πh2
Kadar perubahan tinggi paras air pada ketika tinggi parasnya ialah 0.5m = dhdt.
dhdt=dhdI×dIdt← Petua rantai dhdt=94πh2×0.02← Diberi dIdt=0.02 dhdt=94π(0.5)2×0.02dhdt=0.0572 ms−1
Katakan,
h = tinggi paras air
j = jejari permukaan air
I = isipadu air
jh=0.40.6← Konsep segitiga serupa jh=23j=23h