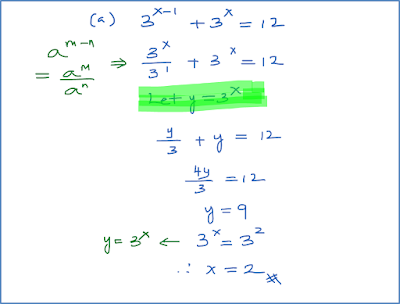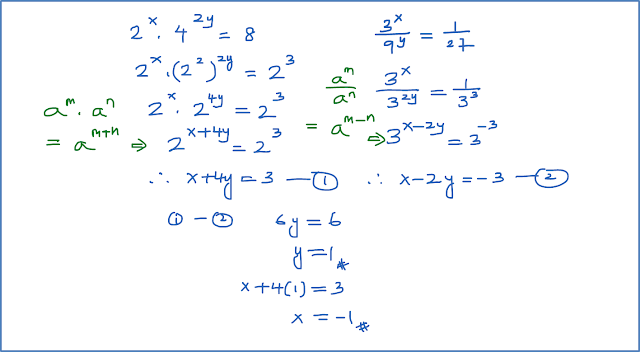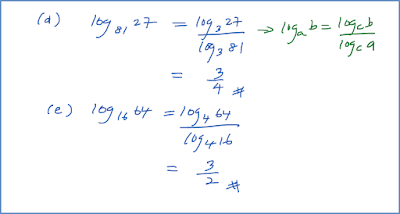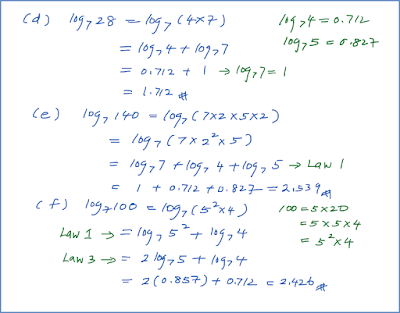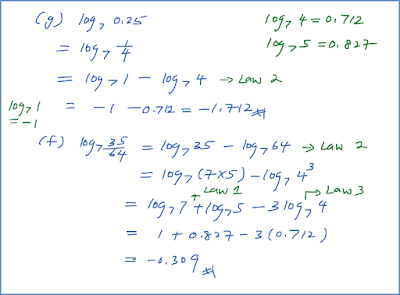Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.5 Indeks dan Logaritma, SPM Praktis (Soalan Pendek)

Soalan 5:

Selesaikan persamaan,

\log_{9} (x - 2) = \log_{3} 2

Penyelesaian:

\begin{array}{l} \log_{9} (x - 2) = \log_{3} 2 \\ \log_{a} b = \frac{\log_{c} b}{\log_{c} a} \Rightarrow \frac{\log_{3} (x - 2)}{\log_{3} 9} = \log_{3} 2 \\ \frac{\log_{3} (x - 2)}{2} = \log_{3} 2 \\ \log_{3} (x - 2) = 2 \log_{3} 2 \\ \log_{3} (x - 2) = \log_{3} 2^{2} \\ x - 2 = 4 \\ x = 6 \end{array}

Soalan 6:

Selesaikan persamaan,

\log_{9} (2 x + 12) = \log_{3} (x + 2)

Penyelesaian:

\begin{array}{l} \log_{9} (2 x + 12) = \log_{3} (x + 2) \\ \frac{\log_{3} (2 x + 12)}{\log_{3} 9} = \log_{3} (x + 2) \\ \log_{3} (2 x + 12) = 2 \log_{3} (x + 2) \\ \log_{3} (2 x + 12) = \log_{3} {(x + 2)}^{2} \\ 2 x + 12 = x^{2} + 4 x + 4 \\ x^{2} + 2 x - 8 = 0 \\ (x + 4) (x - 2) = 0 \\ x = - 4 (tidak diterima) \\ x = 2 \end{array}

Soalan 7:

Selesaikan persamaan,

\log_{4} x = \frac{3}{2} \log_{2} 3

Penyelesaian:

\begin{array}{l} \log_{4} x = \frac{3}{2} \log_{2} 3 \\ \frac{\log_{2} x}{\log_{2} 4} = \frac{3}{2} \log_{2} 3 \\ \frac{\log_{2} x}{2} = \frac{3}{2} \log_{2} 3 \\ \log_{2} x = 2 \times \frac{3}{2} \log_{2} 3 \\ \log_{2} x = 3 \log_{2} 3 \\ \log_{2} x = \log_{2} 3^{3} \\ x = 27 \end{array}

Soalan 8:

Selesaikan persamaan,

\frac{2}{\log_{5} 2} = \log_{2} (2 - x)

Penyelesaian:

\begin{array}{l} \frac{2}{\log_{5} 2} = \log_{2} (2 - x) \\ 2 = \log_{5} 2. \log_{2} (2 - x) \\ 2 = \frac{1}{\log_{2} 5} . \log_{2} (2 - x) \\ 2 \log_{2} 5 = \log_{2} (2 - x) \\ \log_{2} 5^{2} = \log_{2} (2 - x) \\ 25 = 2 - x \\ x = - 23 \end{array}

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.5 Indeks dan Logaritma, SPM Praktis (Soalan Pendek)

Soalan 1:

Selesaikan persamaan, log₃ [log₂(2x – 1)] = 2

Penyelesaian:

log₃ [log₂ (2x – 1)] = 2 ← (jika log _aN = x, N = a^x)

log₂ (2x – 1) = 3²

log₂ (2x – 1) = 9

2x – 1 = 2⁹

x = 256.5

Soalan 2

Selesaikan persamaan,

l o g_{16} [l o g_{2} (5 x - 4)] = l o g_{9} \sqrt{3}

Penyelesaian:

\begin{array}{l} l o g_{16} [l o g_{2} (5 x - 4)] = l o g_{9} \sqrt{3} \\ l o g_{16} [l o g_{2} (5 x - 4)] = \frac{1}{4} \leftarrow \begin{array}{l} \log_{9} \sqrt{3} = \log_{9} 3^{\frac{1}{2}} = \frac{1}{2} \log_{9} 3 \\ = \frac{1}{2} (\frac{1}{\log_{3} 9}) = \frac{1}{2} (\frac{1}{2}) = \frac{1}{4} \end{array} \\ l o g_{2} (5 x - 4) = 16^{\frac{1}{4}} \\ l o g_{2} (5 x - 4) = 2 \\ 5 x - 4 = 2^{2} \\ 5 x = 8 \\ x = \frac{8}{5} \end{array}

Soalan 3

Selesaikan persamaan,

5^{\log_{4} x} = 125

Penyelesaian:

\begin{array}{l} 5^{\log_{4} x} = 125 \\ \log_{5} 5^{\log_{4} x} = \log_{5} 125 \leftarrow \begin{array}{l} ambil log asas 5 \\ di kedua-dua belah \end{array} \\ (\log_{4} x) (\log_{5} 5) = 3 \\ (\log_{4} x) (1) = 3 \\ x = 4^{3} = 64 \end{array}

Soalan 4

Selesaikan persamaan,

5^{\log_{5} (x + 1)} = 9

Penyelesaian:

\begin{array}{l} 5^{\log_{5} (x + 1)} = 9 \\ \log_{5} 5^{^{\log_{5} (x + 1)}} = \log_{5} 9 \\ \log_{5} (x + 1) . \log_{5} 5 = \log_{5} 9 \\ \log_{5} (x + 1) = \log_{5} 9 \\ x + 1 = 9 \\ x = 8 \end{array}

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.3 Persamaan yang Melibatkan Indeks (Contoh Soalan)

Contoh 4 (Persamaan Indeks (Asas Sama) – Penggantian):

Selesaikan setiap persamaan yang berikut.

(a) 3^x ⁻ ¹ + 3^x = 12
(b) 2^x + 2^x ⁺ ³ = 72
(c) 4^x ⁺ ¹ + 2²^x = 20

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.3 Persamaan yang Melibatkan Indeks (Contoh Soalan)

Contoh 3 (Persamaan Indeks – Asas Sama):

Selesaikan setiap persamaan yang berikut.

\begin{array}{l} (a) 27 (81^{3 x}) = 1 \\ (b) \sqrt{81^{n + 2}} = \frac{1}{3^{n} 27^{n - 1}} \\ (c) 8^{x - 1} = \frac{4}{\sqrt{2^{x + 3}}} \end{array}

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.3 Persamaan yang Melibatkan Indeks

Kaedah:
1. Perbandingan indeks dan asas

a. Jika asas adalah sama, apabila a^x = a^y, maka x = y

b. Jika indeks adalah sama, apabila a^x = b^x, maka a = b

2. Mengambil logaritma biasa (Jika asas dan indeks TIDAK sama)

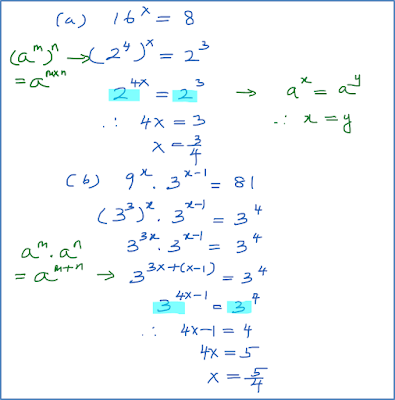
\begin{array}{l} a^{x} = b \Rightarrow \lg a^{x} = \lg b \\ x = \frac{\lg b}{\lg a} \end{array}

Contoh 1 (Persamaan Indeks – Asas Sama):

Selesaikan setiap persamaan yang berikut.

\begin{array}{l} (a) 16^{x} = 8 \\ {(b) 9}^{x} {.3}^{x - 1} = 81 \\ (c) 5^{n + 1} = \frac{1}{125^{n - 1}} \end{array}

Penyelesaian:

Contoh 2 (Selesaikan Persamaan Indeks Serentak – Asas Sama):

Selesaikan persamaan serentak yang berikut.

\begin{array}{l} 2^{x} {.4}^{2 y} = 8 \\ \frac{3^{x}}{9^{y}} = \frac{1}{27} \end{array}

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.2b Penukaran Asas Logaritma (Contoh Soalan)

Contoh 5:

Diberi log₂3 = 1.585 dan log₂5 = 2.322, ungkapkan setiap yang berikut.

(a) log₈ 15

(b) log₅ 0.6

(d) log₁₆ 45

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.2b Penukaran Asas Logaritma (Contoh Soalan)

Contoh 3:

Diberi bahawa log_p3 = h dan log_p 5 = k , ungkapkan setiap yang berikut dalam sebutan h dan k.

\begin{array}{l} (a) \log_{p} \frac{5}{3} \\ (b) \log_{15} 75 \end{array}

Penyelesaian:

Contoh 4:

Diberi bahawa log₃ x = b , ungkapkan log_x 9x dalam sebutan b.

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.2b Penukaran Asas Logaritma

\begin{array}{l} \log_{a} b = \frac{\log_{c} b}{\log_{c} a} \\ dan \\ \log_{a} b = \frac{1}{\log_{b} a} \end{array}

Contoh 1:

Cari nilai-nilai yang berikut:

(a) log₂₅ 100

(b) log₃ 0.45

Penyelesaian:

\begin{array}{l} (a) \log_{25} 100 \\ = \frac{\log_{10} 100}{\log_{10} 25} = \frac{10}{1.3979} = 7.154 \\ (b) \log_{3} 0.45 \\ = \frac{\log_{10} 0.45}{\log_{10} 3} = \frac{- 0.3468}{0.4771} = - 0.727 \end{array}

Contoh 2:

Cari nilai-nilai yang berikut:
(a) log₄ 8
(b) log₁₂₅ 5
(c) log₈₁ 27
(d) log₁₆ 64

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

Contoh 2:

Cari nilai bagi setiap yang berikut.

\begin{array}{l} (a) \log_{2} 7 + \log_{2} 12 + \log_{2} 21 \\ (b) 3 \log_{10} 5 + 2 \log_{10} 2 - \log_{10} 5 \\ (c) 2 \log_{10} 3 - \log_{10} 3 + \log_{10} 3 \frac{1}{3} \\ (d) \log_{3} 3 p + \log_{3} 3 q - \log_{3} p q \end{array}

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.2a Hukum-hukum Logaritma (Contoh 3)

Contoh 3:

Diberi bahawa log₇4 = 0.712 dan log₇5 = 0.827, cari nilai bagi setiap yang berikut.

\begin{array}{l} (a) \log_{7} 20 \\ (b) \log_{7} 1 \frac{1}{4} \\ (c) \log_{7} 0.8 \\ (d) \log_{7} 28 \\ (e) \log_{7} 140 \\ (f) \log_{7} 100 \\ (g) \log_{7} 0.25 \\ (h) \log_{7} \frac{35}{64} \end{array}

Penyelesaian: