Bab 15 Matriks

Posted on May 7, 2016 by user

4.1 Matriks

1. Matriksialah nombor-nombor yang disusun dalam baris dan lajur untuk membentuk satu tatasusunan segi empat tepat.

2. Matriks pada umumnya ditulis dalam tanda kurungan.

Misalnya,

(\begin{matrix} 2 & 0 \\ 3 & 1 \end{matrix})

ialah suatu matriks.

(A) Menentukan billangan baris, bilangan lajur dan peringkat, sesuatu matriks

1. Matriks yang mempunyai mbaris dan n lajurs dikenali sebagai matriks peringkat
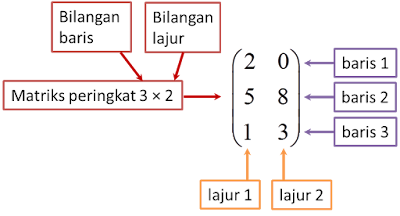
m × n.

2. Matriks baris ialah suatu matriks yang mempunyai hanya satu baris sahaja.

Misalnya:

\begin{array}{l} (4), (2 6), (3 8    5) \\ 1 \times 1 1 \times 2 1 \times 3 \\ ↖ ↑ ↗ \\ Hanya satu baris \end{array}

3. Matriks lajur ialah suatu matriks yang mempunyai hanya satu lajur sahaja.

Misalnya:

\begin{array}{l} (3), (\begin{array}{l} 2 \\ 6 \end{array}), (\begin{array}{l} - 5 \\ 7 \\ - 9 \end{array}) \\ 1 \times 12 \times 13 \times 1 \\ ↖ ↑ ↗ \\ Hanya satu lajur \end{array}

4. Matriks segi empat sama ialah suatu matriks yang mempunyai bilangan baris dan bilangan lajur yang sama.
Misalnya:

\begin{array}{l} (3), (\begin{matrix} 7 & 0 \\ 2 & 5 \end{matrix}), (\begin{matrix} 1 & 39 \\ \begin{array}{l} 0 \\ 6 \end{array} & \begin{array}{l} 41 \\ 35 \end{array} \end{matrix}) \\ 1 \times 12 \times 23 \times 3 \\ ↖ ↑ ↗ \\ Bilangan baris = Bilangan lajur \end{array}

Bab 15 Matriks

Posted on May 7, 2016 by user

4.3 Penambahan dan Penolakan Matriks

(A) Mengenal Pasti Dua Matriks yang boleh ditambah atau ditolak

1. Dua matriks boleh ditambah atau ditolak jika kedua-dua matriks itu mempunyai peringkat yang sama.

2. Penambahan atau penolakan dua matriks yang sama peringkat ialah pembentukan satu matriks yang unsur-unsurnya merupakan hasil tambah (atau hasil tolak) unsur-unsur sepadan dalam dua matriks itu.

Contoh 1:

Tentukan sama ada pasangan matriks yang berikut boleh ditambah atau ditolak. Memberi sebab untuk jawapan anda.

\begin{array}{l} (a) (\begin{array}{l} 2 \\ 3 \end{array}) dan (1 8) \\ (b) (\begin{matrix} 1 & 2 \\ 7 & 1 \end{matrix}) dan (\begin{matrix} 10 & 0 \\ - 3 & - 1 \end{matrix}) \\ (c) (p 2 4) dan (2 6 q) \end{array}

Penyelesaian:

(a) Tidak boleh ditambah atau ditolak kerana peringkat dua matriks itu tidak sama.

(b) Boleh ditambah atau ditolak kerana peringkat dua matriks adalah sama.

(c) Boleh ditambah atau ditolak kerana peringkat dua matriks adalah sama.

Contoh 2:

Ungkapkan setiap yang berikut sebagai satu matriks tunggal.

\begin{array}{l} Diberi A = (\begin{array}{l} 3 \\ 2 \end{array}) dan B = (\begin{array}{l} 5 \\ 1 \end{array}), cari \\ (a) A + B, \\ (b) B - A \end{array}

Penyelesaian:

\begin{array}{l} (a) A + B = (\begin{array}{l} 3 \\ 2 \end{array}) + (\begin{array}{l} 5 \\ 1 \end{array}) \\ = (\begin{array}{l} 3 + 5 \\ 2 + 1 \end{array}) \\ = (\begin{array}{l} 8 \\ 3 \end{array}) \end{array}

\begin{array}{l} (b) B - A = (\begin{array}{l} 3 \\ 2 \end{array}) - (\begin{array}{l} 5 \\ 1 \end{array}) \\ = (\begin{array}{l} 3 - 5 \\ 2 - 1 \end{array}) \\ = (\begin{array}{l} - 2 \\ 1 \end{array}) \end{array}

Bab 15 Matriks

Posted on May 7, 2016 by user

4.8 Penyelesaian Persamaan Linear Serentak dengan Kaedah Matriks

1. Dua persamaan linear serentak boleh ditulis dalam bentuk persamaan matriks.

Sebagai contoh, dalam persamaan linear serentak:

ax+ by = c

dx+ ey = f

boleh ditulis dalam format persamaan matriks seperti berikut:

(\begin{matrix} a & b \\ c & d \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} e \\ f \end{array}),

Di mana a, b, c, d, e dan fadalah pemalar manakala x dan y adalah anu.

Contoh 1:

Tuliskan persamaan linear serentak berikut dalam bentuk persamaan matriks.

y– 6x – 19 = 0

2y + 3x + 22 = 0

Penyelesaian:

– 6x + y = 19

3x + 2y = – 22

Persamaan matriks ialah:

(\begin{matrix} - 6 & 1 \\ 3 & 2 \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 19 \\ - 22 \end{array})

2. Persamaan matriks dalam bentuk

(\begin{matrix} a & b \\ c & d \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} e \\ f \end{array})

dapat diselesaikan bagi anu x dan y seperti berikut.

(a) Katakan

A = (\begin{matrix} a & b \\ c & d \end{matrix})

dan cari A^-1.

(b) Darabkan kedua-dua belah persamaan dengan A^-1.

A^{- 1} (\begin{matrix} a & b \\ c & d \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = A^{- 1} (\begin{array}{l} e \\ f \end{array})

\begin{array}{l} (c) A^{- 1} A (\begin{array}{l} x \\ y \end{array}) = A^{- 1} (\begin{array}{l} e \\ f \end{array}) \\ I (\begin{array}{l} x \\ y \end{array}) = A^{- 1} (\begin{array}{l} e \\ f \end{array}) \\ ↗ \\ A^{- 1} A = I = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) \\ (\begin{array}{l} x \\ y \end{array}) = A^{- 1} (\begin{array}{l} e \\ f \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{a d - b c} (\begin{matrix} d & - b \\ - c & a \end{matrix}) (\begin{array}{l} e \\ f \end{array}) \end{array}

Contoh 2:

Selesaikan persamaan linear serentak berikut dalam bentuk persamaan matriks.

2x = 5 – 3y

7x = 1 – 5y

Penyelesaian:

2x + 3y = 5

7x + 5y = 1

(\begin{matrix} 2 & 3 \\ 7 & 5 \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 5 \\ 1 \end{array}) \leftarrow \begin{array}{l} Tulis persamaan serentak \\ dalam bentuk matriks . \end{array}

\begin{array}{l} Katakan A = (\begin{matrix} 2 & 3 \\ 7 & 5 \end{matrix}) \\ A^{- 1} = \frac{1}{a d - b c} (\begin{matrix} d & - b \\ - c & a \end{matrix}) \\ A^{- 1} = \frac{1}{10 - 21} (\begin{matrix} 5 & - 3 \\ - 7 & 2 \end{matrix}) \\ A^{- 1} = \frac{1}{- 11} (\begin{matrix} 5 & - 3 \\ - 7 & 2 \end{matrix}) \end{array}

(\begin{array}{l} x \\ y \end{array}) = \frac{1}{- 11} (\begin{matrix} 5 & - 3 \\ - 7 & 2 \end{matrix}) (\begin{array}{l} 5 \\ 1 \end{array}) \leftarrow (\begin{array}{l} x \\ y \end{array}) = A^{- 1} (\begin{array}{l} e \\ f \end{array})

\begin{array}{l} (\begin{array}{l} x \\ y \end{array}) = \frac{1}{- 11} (\begin{array}{l} 5 \times 5 + (- 3) \times 1 \\ - 7 \times 5 + 2 \times 1 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{- 11} (\begin{array}{l} 22 \\ - 33 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} - \frac{22}{11} \\ \frac{- 33}{- 11} \end{array}) = (\begin{array}{l} - 2 \\ 3 \end{array}) \\ ∴ x = - 2, y = 3. \end{array}

Bab 15 Matriks

Posted on May 6, 2016 by user

4.5 Pendaraban Dua Matriks (Contoh Soalan)

Soalan 1:

Cari hasil darab bagi setiap pasangan matriks yang berikut.

\begin{array}{l} (a) (1 5 2) (\begin{array}{l} 2 \\ 4 \\ 3 \end{array}) \\ (b) (\begin{matrix} 2 & 8 \\ - 3 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ 4 & - 2 \end{matrix}) \end{array}

\begin{array}{l} (c) (\begin{array}{l} - 3 \\ 5 \end{array}) (2 6) \\ (d) (\begin{matrix} 0 & 4 \\ - 1 & 3 \end{matrix}) (\begin{array}{l} 7 \\ - 2 \end{array}) \\ (e) (7 - 4) (\begin{matrix} - 2 & 0 \\ - 1 & 3 \end{matrix}) \end{array}

Penyelesaian:

\begin{array}{l} (a) \\ (1 5 2) (\begin{array}{l} 2 \\ 4 \\ 3 \end{array}) \leftarrow \begin{array}{l} Analisis matriks \\ 1 \times 3 dan 3 \times 1 \\ ↘ ↙ \\ = matriks 1 \times 1 \end{array} \\ = (1 \times 2 \oplus 5 \times 4 \oplus 2 \times 3) \\ = (2 + 20 + 6) \\ = (28) \end{array}

\begin{array}{l} (b) \\ (\begin{matrix} 2 & 8 \\ - 3 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ 4 & - 2 \end{matrix}) \leftarrow \begin{array}{l} Analisis matriks \\ 2 \times 2 dan 2 \times 2 \\ ↘ ↙ \\ = matriks 2 \times 2 \end{array} \\ = (\begin{matrix} 2 \times 1 + 8 \times 4 & 2 \times 0 + 8 \times - 2 \\ - 3 \times 1 + 1 \times 4 & - 3 \times 0 + 1 \times - 2 \end{matrix}) \\ = (\begin{matrix} 34 & - 16 \\ 1 & - 2 \end{matrix}) \end{array}

\begin{array}{l} (c) \\ (\begin{array}{l} - 3 \\ 5 \end{array}) (2 6) \leftarrow \begin{array}{l} Analisis matriks \\ 2 \times 1 dan 1 \times 2 \\ ↘ ↙ \\ = matriks 2 \times 2 \end{array} \\ = (\begin{matrix} - 3 \times 2 & - 3 \times 6 \\ 5 \times 2 & 5 \times 6 \end{matrix}) \\ = (\begin{matrix} - 6 & - 18 \\ 10 & 30 \end{matrix}) \end{array}

\begin{array}{l} (d) \\ (\begin{matrix} 0 & 4 \\ - 1 & 3 \end{matrix}) (\begin{array}{l} 7 \\ - 2 \end{array}) \leftarrow \begin{array}{l} Analisis matriks \\ 2 \times 2 dan 2 \times 1 \\ ↘ ↙ \\ = matriks 2 \times 1 \end{array} \\ = (\begin{array}{l} 0 \times 7 + 4 \times - 2 \\ - 1 \times 7 + 3 \times - 2 \end{array}) \\ = (\begin{array}{l} - 8 \\ - 13 \end{array}) \end{array}

\begin{array}{l} (e) \\ (7 - 4) (\begin{matrix} - 2 & 0 \\ - 1 & 3 \end{matrix}) \leftarrow \begin{array}{l} Analisis matriks \\ 1 \times 2 dan 2 \times 2 \\ ↘ ↙ \\ = matriks 1 \times 2 \end{array} \\ = (7 \times - 2 + (- 4 \times - 1) 7 \times 0 + (- 4 \times 3)) \\ = (- 14 + 4 0 - 12) \\ = (- 10 - 12) \end{array}

Contoh 2:

Cari nilai mdan nilai n dalam setiap persamaan matriks yang berikut:

(a) (\begin{array}{l} 3 \\ m \end{array}) (1 n) = (\begin{matrix} 3 & 12 \\ - 2 & - 8 \end{matrix})

(b) (\begin{matrix} m & 2 \\ - 3 & 1 \end{matrix}) (\begin{array}{l} 2 \\ n \end{array}) = (\begin{array}{l} 12 \\ 4 + 2 n \end{array})

(c) (\begin{matrix} m & - 3 \\ - 1 & 1 \end{matrix}) (\begin{matrix} - 1 & 2 \\ 4 & n \end{matrix}) = (\begin{matrix} - 14 & - 11 \\ 5 & 3 \end{matrix})

Penyelesaian:

\begin{array}{l} (a) \\ (\begin{array}{l} 3 \\ m \end{array}) (1 4) = (\begin{matrix} 3 & 12 \\ - 2 & n \end{matrix}) \\ (\begin{matrix} 3 & 12 \\ m & 4 m \end{matrix}) = (\begin{matrix} 3 & 12 \\ - 2 & n \end{matrix}) \end{array}

m= –2,

4m = n

4 (–2) = n

n= –8

\begin{array}{l} (b) \\ (\begin{matrix} m & 2 \\ - 3 & 1 \end{matrix}) (\begin{array}{l} 2 \\ n \end{array}) = (\begin{array}{l} 12 \\ 4 + 2 n \end{array}) \\ (\begin{array}{l} 2 m + 2 n \\ - 6 + n \end{array}) = (\begin{array}{l} 12 \\ 4 + 2 n \end{array}) \end{array}

–6 + n = 4 + 2n

n= –10

2m + 2n = 12

2m + 2 (–10) = 12

2m – 20 = 12

2m = 32

m = 16

\begin{array}{l} (c) \\ (\begin{matrix} m & - 3 \\ - 1 & 1 \end{matrix}) (\begin{matrix} - 1 & 2 \\ 4 & n \end{matrix}) = (\begin{matrix} - 14 & - 11 \\ 5 & 3 \end{matrix}) \\ (\begin{matrix} - m + (- 12) & 2 m + (- 3 n) \\ 1 + 4 & - 2 + n \end{matrix}) = (\begin{matrix} - 14 & - 11 \\ 5 & 3 \end{matrix}) \end{array}

–m – 12 = –14

–m = –2

m = 2

–2 + n = 3

n = 5

Bab 15 Matriks

Posted on May 6, 2016 by user

4.5 Pendaraban Dua Matriks

1. Dua matriks hanya boleh didarab apabila bilangan lajur matriks pertama sama dengan bilangan baris matriks kedua.

2. Contohnya, jika Aialah suatu matriks m × n dan Bialah suatu matriks n × t, maka hasil darab matriks AB = P. P ialah suatu matriks, m× t.

Contoh:

\begin{array}{l} (a) (a b) (\begin{array}{l} c \\ d \end{array}) = (a c + b d) \\ 1 \times 22 \times 1 1 \times 1 \\ (b) (\begin{matrix} a & b \\ c & d \end{matrix}) (\begin{array}{l} e \\ f \end{array}) = (\begin{array}{l} a e + b f \\ c e + d f \end{array}) \\ 2 \times 22 \times 12 \times 1 \end{array}

\begin{array}{l} (c) (\begin{matrix} a & b \\ c & d \end{matrix}) (\begin{matrix} e & f \\ g & h \end{matrix}) = (\begin{matrix} a e + b g & a f + b h \\ c e + d g & c f + d h \end{matrix}) \\ 2 \times 22 \times 22 \times 2 \\ (d) (\begin{array}{l} a \\ b \end{array}) (c d) = (\begin{matrix} a c & a d \\ b c & b d \end{matrix}) \\ 2 \times 11 \times 22 \times 2 \end{array}

\begin{array}{l} (e) (a b c) (\begin{array}{l} d \\ e \\ f \end{array}) = (a d + b e + c f) \\ 1 \times 33 \times 11 \times 1 \\ (f) (\begin{matrix} a & b \\ \begin{array}{l} c \\ e \end{array} & \begin{array}{l} d \\ f \end{array} \end{matrix}) (\begin{array}{l} g \\ h \end{array}) = (\begin{array}{l} a g + b h \\ c g + d h \\ e g + f h \end{array}) \\ 3 \times 22 \times 13 \times 1 \end{array}

Contoh 1:

Tentukan sama ada hasil darab matriks yang berikut boleh dialakukan atau tidak. Jika boleh, nyatakan peringkat matriks yang terhasil.

\begin{array}{l} (a) (\begin{matrix} 3 & - 5 \\ 1 & 2 \end{matrix}) (3 7) \\ (b) (\begin{matrix} 2 & 9 \\ 1 & 3 \end{matrix}) (\begin{array}{l} 8 \\ 6 \end{array}) \\ (c) (- 10 - 6) (\begin{array}{l} 7 \\ 2 \end{array}) \\ (d) (\begin{array}{l} 8 \\ 6 \end{array}) (\begin{matrix} 2 & 9 \\ 1 & 3 \end{matrix}) \\ (e) (\begin{array}{l} 7 \\ - 3 \end{array}) (2 10) \end{array}

Penyelesaian:

\begin{array}{l} (a) (\begin{matrix} 3 & - 5 \\ 1 & 2 \end{matrix}) (3 7) \\ 2 \times 2 1 \times 2 \leftarrow 2 \neq 1 ∴ Tidak boleh didarab . \end{array}

\begin{array}{l} b) (\begin{matrix} 2 & 9 \\ 1 & 3 \end{matrix}) (\begin{array}{l} 8 \\ 6 \end{array}) \\ 2 \times 2 2 \times 1 \leftarrow 2 = 2 ∴ Boleh didarab . \\ Peringkat matriks yang terhasil = 2 \times 1 \end{array}

\begin{array}{l} (c) (- 10 - 6) (\begin{array}{l} 7 \\ 2 \end{array}) \\ 1 \times 2 2 \times 1 \leftarrow 2 = 2 ∴ Boleh didarab . \\ Peringkat matriks yang terhasil = 1 \times 1 \end{array}

\begin{array}{l} (d) (\begin{array}{l} 8 \\ 6 \end{array}) (\begin{matrix} 2 & 9 \\ 1 & 3 \end{matrix}) \\ 2 \times 1 2 \times 2 \leftarrow 1 \neq 2 ∴ Tidak boleh didarab . \end{array}

\begin{array}{l} (e) (\begin{array}{l} 7 \\ - 3 \end{array}) (2 10) \\ 2 \times 1 1 \times 2 \leftarrow 1 = 1 ∴ Boleh didarab . \\ Peringkat matriks yang terhasil = 2 \times 2 \end{array}

Bab 15 Matriks

Posted on May 6, 2016 by user

4.4 Pendaraban Matriks dengan Nombor (Contoh Soalan)

Contoh 1:

Ungkapkan setiap yang berikut sebagai satu matriks tunggal.

(a) 3 (\begin{matrix} 1 & - 4 \\ - 3 & 2 \end{matrix}) + 2 (\begin{matrix} - 3 & 1 \\ 3 & - 4 \end{matrix})

(b) 2 (\begin{matrix} - 1 & 0 \\ 9 & - 4 \end{matrix}) - 4 (\begin{matrix} - 2 & 2 \\ 3 & - 6 \end{matrix}) - \frac{1}{3} (\begin{matrix} - 9 & - 3 \\ - 6 & 15 \end{matrix})

Penyelesaian:

\begin{array}{l} (a) 3 (\begin{matrix} 1 & - 4 \\ - 3 & 2 \end{matrix}) + 2 (\begin{matrix} - 3 & 1 \\ 3 & - 4 \end{matrix}) \\ = (\begin{matrix} 3 \times 1 & 3 \times (- 4) \\ 3 \times (- 3) & 3 \times 2 \end{matrix}) + (\begin{matrix} 2 \times (- 3) & 2 \times 1 \\ 2 \times 3 & 2 \times (- 4) \end{matrix}) \\ = (\begin{matrix} 3 & - 12 \\ - 9 & 6 \end{matrix}) + (\begin{matrix} - 6 & 2 \\ 6 & - 8 \end{matrix}) \\ = (\begin{matrix} 3 + (- 6) & - 12 + 2 \\ - 9 + 6 & 6 - (- 8) \end{matrix}) \\ = (\begin{matrix} - 3 & - 10 \\ - 3 & 14 \end{matrix}) \end{array}

\begin{array}{l} (b) 2 (\begin{matrix} - 1 & 0 \\ 9 & - 4 \end{matrix}) - 4 (\begin{matrix} - 2 & 2 \\ 3 & - 6 \end{matrix}) - \frac{1}{3} (\begin{matrix} - 9 & - 3 \\ - 6 & 15 \end{matrix}) \\ = (\begin{matrix} - 2 & 0 \\ 18 & - 8 \end{matrix}) - (\begin{matrix} - 8 & 8 \\ 12 & - 24 \end{matrix}) - (\begin{matrix} \frac{1}{3} \times (- 9) & \frac{1}{3} \times (- 3) \\ \frac{1}{3} \times (- 6) & \frac{1}{3} \times 15 \end{matrix}) \\ = (\begin{matrix} - 2 & 0 \\ 18 & - 8 \end{matrix}) - (\begin{matrix} - 8 & 8 \\ 12 & - 24 \end{matrix}) - (\begin{matrix} - 3 & - 1 \\ - 2 & 5 \end{matrix}) \\ = (\begin{matrix} - 2 - (- 8) - (- 3) & 0 - 8 - (- 1) \\ 18 - 12 - (- 2) & - 8 - (- 24) - 5 \end{matrix}) \\ = (\begin{matrix} 9 & - 7 \\ 10 & 11 \end{matrix}) \end{array}

Bab 15 Matriks

Posted on May 6, 2016 by user

4.4 Pendaraban Matriks dengan Nombor

Pendaraban suatu matriks dengan suatu nombor ialah pendaraban setiap unsur matriks dengan nombor itu.

Contoh:

Diberi

A = (\begin{matrix} - 2 & 4 \\ 5 & - 6 \end{matrix})

, cari setiap yang berikut sebagai satu matriks tunggal.

(a) 3A

(b) -2A

Penyelesaian:

\begin{array}{l} (a) 3 A = 3 (\begin{matrix} - 2 & 4 \\ 5 & - 6 \end{matrix}) \\ = (\begin{matrix} 3 \times (- 2) & 3 \times 4 \\ 3 \times 5 & 3 \times (- 6) \end{matrix}) \\ = (\begin{matrix} - 6 & 12 \\ 15 & - 18 \end{matrix}) \end{array}

\begin{array}{l} (b) - 2 A = - 2 (\begin{matrix} - 2 & 4 \\ 5 & - 6 \end{matrix}) \\ = (\begin{matrix} - 2 \times (- 2) & - 2 \times 4 \\ - 2 \times 5 & - 2 \times (- 6) \end{matrix}) \\ = (\begin{matrix} - 4 & - 8 \\ - 10 & 12 \end{matrix}) \end{array}

Bab 15 Matriks

Posted on May 6, 2016 by user

4.3 Penambahan dan Penolakan Matriks (Contoh Soalan)

Contoh 1:

Cari hasil tambah bagi matriks yang berikut:

\begin{array}{l} (a) (18 - 7) + (3 6) \\ (b) (\begin{matrix} - 13 & 0 \\ 7 & - 1 \end{matrix}) + (\begin{matrix} - 1 & 3 \\ 5 & 6 \end{matrix}) \end{array}

Penyelesaian:

\begin{array}{l} (a) (18 - 7) + (3 6) \\ = (18 + 3 - 7 + 6) = (21 - 1) \\ (b) (\begin{matrix} - 13 & 0 \\ 7 & - 1 \end{matrix}) + (\begin{matrix} - 1 & 3 \\ 5 & 6 \end{matrix}) \\ = (\begin{matrix} - 13 + (- 1) & 0 + 3 \\ 7 + 5 & - 1 + 6 \end{matrix}) = (\begin{matrix} - 14 & 3 \\ 12 & 5 \end{matrix}) \end{array}

Contoh 2:

Cari setiap yang berikut sebagai satu matriks tunggal.

\begin{array}{l} (a) (\begin{array}{l} 9 \\ 6 \end{array}) - (\begin{array}{l} 7 \\ - 2 \end{array}) \\ (b) (\begin{matrix} 3 & - 4 \\ 0 & 5 \end{matrix}) - (\begin{matrix} - 7 & - 3 \\ - 6 & 1 \end{matrix}) \end{array}

Penyelesaian:

\begin{array}{l} (a) (\begin{array}{l} 9 \\ 6 \end{array}) - (\begin{array}{l} 7 \\ - 2 \end{array}) = (\begin{array}{l} 9 - 7 \\ 6 - (- 2) \end{array}) = (\begin{array}{l} 2 \\ 8 \end{array}) \\ (b) (\begin{matrix} 3 & - 4 \\ 0 & 5 \end{matrix}) - (\begin{matrix} - 7 & - 3 \\ - 6 & 1 \end{matrix}) \\ = (\begin{matrix} 3 - (- 7) & - 4 - (- 3) \\ 0 - (- 6) & 5 - 1 \end{matrix}) \\ = (\begin{matrix} 3 + 7 & - 4 + 3 \\ 0 + 6 & 5 - 1 \end{matrix}) = (\begin{matrix} 10 & - 1 \\ 6 & 4 \end{matrix}) \end{array}

(B) Menentukan nilai unsur yang tidak diketahui dalam persamaan matriks yang melibatkan operasi tambah dan tolak

Contoh 3:

Diberi

(\begin{array}{l} p \\ q \end{array}) + (\begin{array}{l} 5 p \\ 9 \end{array}) = (\begin{array}{l} - 12 \\ 3 q + 1 \end{array})

, cari nilai bagi p dan q.

Penyelesaian:

\begin{array}{l} (\begin{array}{l} p \\ q \end{array}) + (\begin{array}{l} 5 p \\ 9 \end{array}) = (\begin{array}{l} - 12 \\ 3 q + 1 \end{array}) \\ (\begin{array}{l} p + 5 p \\ q + 9 \end{array}) = (\begin{array}{l} - 12 \\ 3 q + 1 \end{array}) \\ p + 5 p = - 12 \\ 6 p = - 12 \\ p = - 2 \end{array}

\begin{array}{l} q + 9 = 3 q + 1 \\ q - 3 q = 1 - 9 \\ - 2 q = - 8 \\ q = 4 \end{array}

Contoh 4:

Cari nilai m dan n bagi persamaan matriks yang berikut:

(\begin{matrix} 7 & 6 \\ n & 1 \end{matrix}) - (\begin{matrix} - 1 & m \\ - 4 & - 2 \end{matrix}) = (\begin{matrix} 5 & 12 \\ 6 & 11 \end{matrix})

Penyelesaian:

\begin{array}{l} (\begin{matrix} 7 & 6 \\ n & 1 \end{matrix}) - (\begin{matrix} - 1 & m \\ - 4 & - 2 \end{matrix}) = (\begin{matrix} 5 & 12 \\ 6 & 11 \end{matrix}) \\ 6 - m = 12 \\ - m = 6 \\ m = - 6 \\ n - (- 4) = 6 \\ n + 4 = 6 \\ n = 2 \end{array}

Bab 15 Matriks

Posted on May 6, 2016 by user

4.2 Matriks Sama (Contoh Soalan)

Contoh 1:

(\begin{matrix} 1 & x + 2 \\ 4 - y & - 1 \end{matrix}) = (\begin{matrix} 1 & 3 \\ 2 & - 1 \end{matrix})

Penyelesaian:

\begin{array}{l} (\begin{matrix} 1 & x + 2 \\ 4 - y & - 1 \end{matrix}) = (\begin{matrix} 1 & 3 \\ 2 & - 1 \end{matrix}) \\ x + 2 = 3 \\ x = 1 \\ 4 - y = 2 \\ - y = - 2 \\ y = 2 \end{array}

Contoh 2:

Hitung nilai p dan nilai q dalam setiap persamaan matriks yang berikut:

\begin{array}{l} (a) (\begin{matrix} 3 & 2 p + q \\ p & - 3 \end{matrix}) = (\begin{matrix} 3 & 1 \\ 8 - 2 q & - 3 \end{matrix}) \\ (b) (\begin{matrix} 10 & 0 \\ 5 p - 8 & 1 \end{matrix}) = (\begin{matrix} p - 2 q & 0 \\ - 4 q & 1 \end{matrix}) \end{array}

Penyelesaian:

(a) (\begin{matrix} 3 & 2 p + q \\ p & - 3 \end{matrix}) = (\begin{matrix} 3 & 1 \\ 8 - 2 q & - 3 \end{matrix})

2p + q = 1

q= 1 – 2p ----(1)

p= 8 – 2q ----(2)

Gantikan (1) ke dalam (2),

p= 8 – 2 (1 – 2p)

p= 8 – 2 + 4p

p– 4p = 6

–3p = 6

p= –2

Gantikan p= –2 ke dalam (1),

q= 1 – 2(–2)

q= 5

(b) (\begin{matrix} 10 & 0 \\ 5 p - 8 & 1 \end{matrix}) = (\begin{matrix} p - 2 q & 0 \\ - 4 q & 1 \end{matrix})

10 = p – 2 q

p= 10 + 2q ----(1)

5p – 8 = –4q ----(2)

Gantikan (1) ke dalam (2),

5 (10 + 2q) – 8 = –4q

50 + 10q – 8 = –4q

14q = –42

q= –3

Gantikan q= –3 ke dalam (1),

p= 10 + 2(–3)

p= 4

Bab 14 Penjelmaan

Posted on May 5, 2016 by user

3.1d Menghuraikan Gabungan Dua Penjelmaan

Contoh 1:

Dalam rajah di atas, segi tiga KLM, ialah imej bagi segi tiga ABC di bawah gabungan penjelmaan VW. Huraikan selengkapnya penjelmaan W dan penjelmaan V.

Penyelesaian:

Segi tiga ABC → W→ Segi tiga KB’C’ → V → Segi tiga KLM

W = Translasi (\begin{array}{l} 0 \\ 4 \end{array})

V = Pembesaran pada pusat K (1, 1) dengan faktor skala 3.

Contoh 2:

Dalam rajah di atas, segi tiga CKL, ialah imej bagi segi tiga ABC di bawah gabungan penjelmaan UY. Huraikan selengkapnya penjelmaan Y dan penjelmaan U.

Penyelesaian:

Segi tiga ABC → Y→ Segi tiga AB’C → U→ Segi tiga CKL

Y = Pantulan pada garis lurus y = 6

U = Pembesaran pada pusat C (12, 6) dengan faktor skala 2.

Contoh 3:

Dalam rajah di atas, segi tiga PQR, ialah imej bagi segi tiga ABC di bawah gabungan penjelmaan TW.
Huraikan selengkapnya penjelmaan W dan penjelmaan T.

Penyelesaian:

Segi tiga ABC → W→ Segi tiga PBC’ → T→ Segi tiga PQR

W = Putaran ikut arah jam melalui 90^o pada pusat B (5, 5).

T = Pembesaran pada pusat P (1, 5) dengan faktor skala 2.