Bab 6 Geometri Koordinat

Posted on May 25, 2016 by user

6.4.1 Persamaan Garis Lurus (Bahagian 1)

(A) Pintasan pada Paksi dan Kecerunan

1. Kecerunan garis lurus melalui titik (x₁, y_l) dan titik (x₂, y₂) ialah

m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}

2. Kecerunan garis lurus dengan pintasan-x dan pintasan-y diketahui ialah:

m = - \frac{pintasan y}{pintasan x}

(B) Titik-titik Segaris

Kecerunan garis lurus adalah sentiasa malar; iaitu kecerunan AB sama dengan kecerunan BC.

m_AB=m_BC= m_AC

Contoh 1:

Kecerunan garis lurus yang melalui titik (k, 1 – k) dan titik (–3k, –3) ialah 5. Cari nilai k.

Penyelesaian:

\begin{array}{l} Kecerunan, m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ \frac{- 3 - (1 - k)}{- 3 k - k} = 5 \\ \frac{- 3 - 1 + k}{- 4 k} = 5 \\ - 4 + k = - 20 k \\ 21 k = 4 \\ k = \frac{4}{21} \end{array}

Contoh 2:

Berdasarkan rajah di bawah, cari nilai kecerunan garis lurus.

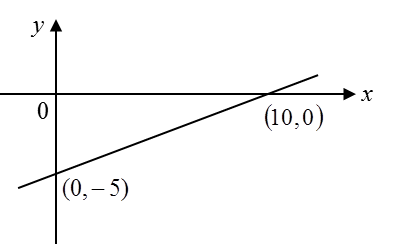
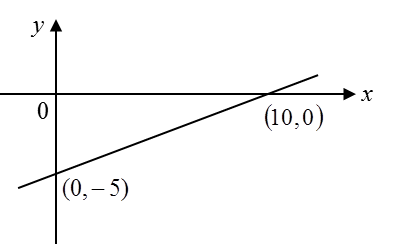
Penyelesaian:

\begin{array}{l} Kecerunan, m = - (\frac{pintasan y}{pintasan x}) \\ = - (\frac{- 5}{10}) \\ = \frac{1}{2} \end{array}

Bab 6 Geometri Koordinat

Posted on May 25, 2016 by user

6.3 Luas Poligon

(A) Luas Segitiga

Rumus Luas Segitiga

\begin{array}{l} = \frac{1}{2} | \begin{array}{l} x_{1} x_{2} x_{3} \\ y_{1} y_{2} y_{3} \end{array} \begin{array}{l} x_{1} \\ y_{1} \end{array} | \\ = \frac{1}{2} | (x_{1} y_{2} + x_{2} y_{^{3}} + x_{3} y_{1}) - (y_{1} x_{2} + y_{2} x_{3} + y_{3} x_{1}) | \end{array}

1. Apabila koordinat bucu ditulis dalam susunan lawan arah jam, luas yang terhasil adalah positif. Luas segitiga bernilai negatif jika susunan mengikut arah jam. Walau bagaimanapun luas jawapan mesti diberi dalam nilai positif.

Contoh 1:

Hitungkan luas ∆ABC dengan bucu-bucu A(-5, 5), B (-2, -4), C (4, -1).

Penyelesaian:

Luas ∆ ABC

= \frac{1}{2} | \begin{array}{l} - 5 - 2 4 \\ 5 - 4 - 1 \end{array} \begin{array}{l} - 5 \\ 5 \end{array} |

= ½│(–5)( –4) + (–2)( –1) + (4)(5) – (5)( –2) – (–4)(4) – (–1)( –5)│

= ½│20 + 2 + 20 + 10 + 16 – 5│

= ½│63│

= 31½ unit²

(B) Luas Segiempat

Rumus Luas Segiempat, L

\begin{array}{l} = \frac{1}{2} | \begin{array}{l} x_{1} x_{2} x_{3} x_{4} \\ y_{1} y_{2} y_{3} y_{4} \end{array} \begin{array}{l} x_{1} \\ y_{1} \end{array} | \\ = \frac{1}{2} | (x_{1} y_{2} + x_{2} y_{3} + x_{3} y_{4} + x_{4} y_{1}) - (y_{1} x_{2} + y_{2} x_{3} + y_{3} x_{4} + y_{4} x_{1}) | \end{array}

(C) Jika titik-titik A, Bdan C adalah segaris, maka luas ∆ABC adalah 0.

Contoh 2:

Cari nilai k jika titik-titik P (2, 1), Q (6, k) dan R (3k, 9/2) adalah segaris.

Penyelesaian:

Luas ∆ PQR = 0

\frac{1}{2} | \begin{array}{l} 2 63 k \\ 1 k \frac{9}{2} \end{array} \begin{array}{l} 2 \\ 1 \end{array} | = 0

½│2k + 27 + 3k –6 – 3k² – 9│= 0

│–3k² + 5k + 12│= 0

3k² – 5k – 12 = 0

(3k + 4)(k – 3) = 0

Bab 6 Geometri Koordinat

Posted on May 25, 2016 by user

6.2 Pembahagian Tembereng Garis

(A) Titik Tengah di antara Dua Titik

Rumus titik tengah, Mbagi titik A(x_l, y₁) dan titik B(x₂, y₂) ialah

M = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})

Contoh 1:

Diberi B (m – 4, 3) ialah titik tengah bagi garis lurus yang menyambungkan A (–1, n) dan C (5, 8). Cari nilai m dan nilai n.

Penyelesaian:

B ialah titik tengah AC

\begin{array}{l} (m - 4, 3) = (\frac{- 1 + 5}{2}, \frac{n + 8}{2}) \\ (m - 4, 3) = (2, \frac{n + 8}{2}) \\ m - 4 = 2 dan \frac{n + 8}{2} = 3 \\ m = 6 dan n + 8 = 6 \\ n = - 2 \end{array}

(B) Titik yang Membahagikan dalam Sesuatu Tembereng Garis dengan Nisbah m : n

Rumus untuk titik terletak atas AB dengan keadaan AP : PB = m : n ialah

P = (\frac{n x_{1} + m x_{2}}{m + n}, \frac{n y_{1} + m y_{2}}{m + n})

Contoh 2:

Koordinat R (2, –1) membahagi dalam garis AB dengan nisbah 3 : 2. jika koordinat A ialah (–1, 2), cari koordinat B.

Penyelesaian:

Katakan titik B = (p, q)

\begin{array}{l} (\frac{2 (- 1) + 3 p}{3 + 2}, \frac{2 (2) + 3 q}{3 + 2}) = (2, - 1) \\ (\frac{- 2 + 3 p}{5}, \frac{4 + 3 q}{5}) = (2, - 1) \end{array}

Menyamakan koordinat-koordinat x,

\frac{- 2 + 3 p}{5} = 2

–2 + 3p = 10

3p = 12

p = 4

Menyamakan koordinat-koordinat y,

\frac{4 + 3 q}{5} = - 1

4 + 3q = –5

3q = –9

q = –3

Maka, koordinat-koordinat titik B = (4, –3)

Bab 6 Geometri Koordinat

Posted on May 25, 2016 by user

6.1 Jarak di antara Dua Titik

A(x₁, y₁) dan C (x₂, y₂) adalah dua titik atas satah koordinat seperti ditunjukkan di bawah. BC selari dengan paksi-x dan AB selari dengan paksi-y. Seterusnya ∆ABC= 90°.

Jarak antara titik A dan titik C =

= \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}

Contoh:

Cari jarak di antara titik P (2, –2) dan titik Q (–4, –5).

Penyelesaian:

Katakan P (2, –2) = (x₁, y₁) dan Q (–4, –5) = (x₂, y₂).

\begin{array}{l} Jarak P Q \\ = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}} \\ = \sqrt{{(- 4 - 2)}^{2} + {(- 5 - (- 2))}^{2}} \\ = \sqrt{36 + 9} \\ = \sqrt{45} \\ = \sqrt{9 \times 5} \\ = 3 \sqrt{5} or (6.71) unit \end{array}

Bab 6 Geometri Koordinat

Posted on May 24, 2016 by user

6.7 Geometri Koordinat, SPM Praktis (Soalan Pendek)

Soalan 1:

Bucu-bucu sebuah segitiga ialah P (6, 1), Q (5, 6) dan R (m, –1). Diberi luas segitiga itu ialah 31 unit², cari nilai-nilai m.

Penyelesaian:

Luas segitiga PQR = 31

\frac{1}{2} | \begin{array}{l} 6     5 m \\ 1     6 - 1 \end{array} \begin{array}{l} 6 \\ 1 \end{array} | = 31

│(6)(6) + (5)( –1) + (m)(1) – (1)(5) – (6)(m) – (–1)(6)│= 62

│36 – 5 + m – 5 – 6m + 6│= 62

│32 – 5m│= 62

32 – 5m = ±62

–5m = 62 – 32 atau –5m = –62 – 32

m = –6

m = \frac{94}{5}

Soalan 2:

Titik-titik P(3m, m), Q(t, u) dan R(3t, 2u) terletak pada satu garis lurus. Q membahagi dalam PR dengan nisbah 3: 2.

Ungkap t dalam sebutan u.

Penyelesaian:

\begin{array}{l} (\frac{(3 m) (2) + (3 t) (3)}{3 + 2}, \frac{(m) (2) + (2 u) (3)}{3 + 2}) = (t, u) \\ \frac{6 m + 9 t}{5} = t \\ 6 m + 9 t = 5 t \\ 6 m = - 4 t \\ m = - \frac{2}{3} t \to (1) \end{array}

\begin{array}{l} \frac{2 m + 6 u}{5} = u \\ 2 m + 6 u = 5 u \\ 2 m = - u \\ Daripada (1), \\ 2 (- \frac{2 t}{3}) = - u \\ t = \frac{3}{4} u \end{array}

Bab 15 Vektor

Posted on May 24, 2016 by user

4.4 Pengungkapan Suatu Vektor sebagai Gabungan Linear Vektor yang lain

1. Hukum Poligon Vektor

\vec{P Q} = \vec{P U} + \vec{U T} + \vec{T S} + \vec{S R} + \vec{R Q}

2. Untuk membuktikan dua vector adalah selari, kita mesti mengungkapkan salah satu vector sebagai kuantiti scalar kepada vector yang lain.

Misalnya,

\vec{A B} = k \vec{C D} atau \vec{C D} = h \vec{A B} .

3. Untuk membuktikan titik P, Q dan R adalah segaris, buktikan salah satu daripada berikut:

\begin{array}{l} • \vec{P Q} = k \vec{Q R} atau \vec{Q R} = h \vec{P Q} \\ • \vec{P R} = k \vec{P Q} atau \vec{P Q} = h \vec{P R} \\ • \vec{P R} = k \vec{Q R} atau \vec{Q R} = h \vec{P R} \end{array}

Bab 15 Vektor

Posted on May 24, 2016 by user

4.2 Pendaraban Vektor dengan Kuantiti Skalar dan Keselarian Vektor

1. Hasil darab vektor

\underset{˜}{a}

dengan suatu scalar k ialah

k \underset{˜}{a}

2. Jika

\underset{˜}{b} = k \underset{˜}{a}

, vector

\underset{˜}{b}

adalah searah dengan vector

\underset{˜}{a}

dan magnitudnya,

| \underset{˜}{b} | = k | \underset{˜}{a} | .

3. Vektor

\underset{˜}{a}

adalah selari dengan vektor

\underset{˜}{b}

jika dan hanya jika

\underset{˜}{b} = λ \underset{˜}{a}

, dengan keadaan λialah pemalar.

4. Jika vektor

\underset{˜}{a} dan \underset{˜}{b}

tidak selari dan

h \underset{˜}{a} = k \underset{˜}{b}

, maka h = 0 dan k = 0.

Contoh 1:

Jika vektor

\underset{˜}{a} dan \underset{˜}{b}

tidak selari dan

(k - 7) \underset{˜}{a} = (5 + h) \underset{˜}{b}

, cari nilai k dan nilai h.

Penyelesaian:

Vektor

\underset{˜}{a} dan \underset{˜}{b}

tidak selari, maka

k – 7 = 0 → k= 7

5 + h = 0 → h = –5

Bab 15 Vektor

Posted on May 24, 2016 by user

4.3 Penambahan dan Penolakan Vektor

4.3.1 Penambahan Vektor

1. Penambahan dua vektor,

\underset{˜}{u} dan \underset{˜}{v}

, boleh ditulis sebagai

\underset{˜}{u} + \underset{˜}{v}

. Hasil tambah ini merupakan suatu vektor, yang dinamakan vector paduan.

2. Apabila dua vektor yang sama ditambah, vector paduan yang terhasil mempunyai

(a) arah yang sama dengan kedua-dua vektor itu,

(b) magnitude yang sama dengan hasil tambah magnitud kedua-dua vektor itu.

(A) Penambahan Vektor Paduan Dua Vektor Tidak Selari

1. Penambahan dua vektor yang tidak selari,

\underset{˜}{u} dan \underset{˜}{v}

, boleh ditunjukkan dengan dua hukum.

(i) Hukum Segitiga

Vektor paduan

\underset{˜}{u} + \underset{˜}{v}

yang terhasil ialah AC.

(ii) Hukum Segiempat Selari

Vektor paduan

\underset{˜}{u} + \underset{˜}{v}

yang terhasil ialah AC.

Contoh 1:

Cari

(a) vector paduan hasil tambah bagi dua vector selari yang di atas.

(b) magnitud bagi vector paduan.

Penyelesaian:

(a)

Vektor paduan

= hasil tambah dua vektor

= \vec{P Q} + \vec{R S}

(b)

Magnitud bagi vector paduan

\begin{array}{l} = | \vec{P Q} | + | \vec{R S} | \\ = | \sqrt{6^{2} + 8^{2}} | + | \sqrt{6^{2} + 8^{2}} | \\ = 10 + 10 \\ = 20 units \end{array}

Contoh 2:

Rajah di atas menunjukkan suatu segiempat selari OABC. M adalah titik tengah BC. Vektor

\vec{O A} = \underset{˜}{a} dan \vec{O C} = \underset{˜}{c} .

Cari setiap vektor yang berikut dalam sebutan

\underset{˜}{a} dan \underset{˜}{c} .

\begin{array}{l} (a) \vec{O B} \\ (b) \vec{M B} \\ (c) \vec{O M} \end{array}

Penyelesaian:

(a)

\begin{array}{l} \vec{O B} = \vec{O A} + \vec{A B} \leftarrow Hukum segitiga \\ = \vec{O A} + \vec{O C} \leftarrow \vec{A B} = \vec{O C} \\ = \underset{˜}{a} + \underset{˜}{c} \end{array}

(b)

\begin{array}{l} \vec{M B} = \frac{1}{2} \vec{C B} \leftarrow M adalah titik tengah C B \\ = \frac{1}{2} \vec{O A} \\ = \frac{1}{2} \underset{˜}{a} \end{array}

(c)

\begin{array}{l} \vec{O M} = \vec{O C} + \vec{C M} \leftarrow Hukum segitiga \\ = \vec{O C} + \vec{M B} \leftarrow \vec{C M} = \vec{M B} \\ = \underset{˜}{c} + \frac{1}{2} \underset{˜}{a} \end{array}

Bab 15 Vektor

Posted on May 24, 2016 by user

4.3 Penambahan dan Penolakan Vektor

4.3.2 Penolakan Dua Vektor

Penolakan vektor

\underset{˜}{b}

dari vektor

\underset{˜}{a}

ditulis sebagai

\underset{˜}{a} - \underset{˜}{b}

. Operasi ini juga merupakan penambahan vektor

\underset{˜}{a}

dengan vektor negatif

\underset{˜}{b}

. Oleh itu

\underset{˜}{a} - \underset{˜}{b} = \underset{˜}{a} + (- \underset{˜}{b}) .

Contoh 1:

Dalam rajah di atas, vektor

\vec{O P} = \underset{˜}{p}, \vec{O R} = \underset{˜}{r}

dan Q membahagikan PR dalam nisbah 2: 3. Cari vektor-vektor berikut dalam sebutan

\underset{˜}{p} dan \underset{˜}{r}

\begin{array}{l} (a) \vec{P R} \\ (b) \vec{O Q} \\ (c) \vec{Q M} jika M ialah titik tengah O R . \end{array}

Penyelesaian:

(a)

\begin{array}{l} \vec{P R} = \vec{P O} + \vec{O R} \\ = - \vec{O P} + \vec{O R} \\ = - \underset{˜}{p} + \underset{˜}{r} \end{array}

(b)

\begin{array}{l} \vec{O Q} = \vec{O P} + \vec{P Q} \\ = \vec{O P} + \frac{2}{5} \vec{P R} \\ = \underset{˜}{p} + \frac{2}{5} (- \underset{˜}{p} + \underset{˜}{r}) \\ = \underset{˜}{p} - \frac{2}{5} \underset{˜}{p} + \frac{2}{5} \underset{˜}{r} \\ = \frac{3}{5} \underset{˜}{p} + \frac{2}{5} \underset{˜}{r} \end{array}

(c)

\begin{array}{l} \vec{Q M} = \vec{Q O} + \vec{O M} \\ = - \vec{O Q} + \vec{O M} \\ = - \vec{O Q} + \frac{1}{2} \vec{O R} \\ = - (\frac{3}{5} \underset{˜}{p} + \frac{2}{5} \underset{˜}{r}) + \frac{1}{2} \underset{˜}{r} \\ = - \frac{3}{5} \underset{˜}{p} - \frac{2}{5} \underset{˜}{r} + \frac{1}{2} \underset{˜}{r} \\ = - \frac{3}{5} \underset{˜}{p} + \frac{1}{10} \underset{˜}{r} \end{array}

Bab 14 Pengamiran

Posted on May 23, 2016 by user

3.1 Pengamiran Sebagai Songsangan Pembezaan

1. Pengamiran ialah process songsangan pembezaan.

Jika \frac{d y}{d x} = f (x), maka \int f (x) d x = y .

(A) Pengamiran Pemalar

\int a d x = a x + c

Contoh:

\int 2 d x = 2 x + c

(B) Pengamiran axⁿ

\int a x^{n} d x = \frac{a x^{n + 1}}{n + 1} + c

Contoh 1:

\int 2 x^{3} d x = \frac{2 x^{4}}{4} + c = \frac{x^{4}}{2} + c

Contoh 2:

\begin{array}{l} \int \frac{2}{3 x^{5}} d x = \int \frac{2}{3} x^{- 5} d x \\ = \frac{2}{3} (\frac{x^{- 4}}{- 4}) + c \\ = \frac{2}{3} (\frac{x^{- 4}}{- 4}) + c \\ = \frac{x^{- 4}}{- 6} + c \end{array}

(C) Pengamiran Fungsi berbentuk Hasil Tambah Sebutan Algebra

\begin{array}{l} \int (u \pm v) d x = \int u d x \pm \int v d x \\ u dan v adalah fungsi dalam x \end{array}

Contoh 1:

\begin{array}{l} \int 3 x^{2} + 2 x d x \\ = \int 3 x^{2} d x + \int 2 x d x \\ = \frac{3 x^{3}}{3} + \frac{2 x^{2}}{2} + c \\ = \frac{3 x^{3}}{3} + \frac{2 x^{2}}{2} + c \\ = x^{3} + x^{2} + c \end{array}

Contoh 2:

\begin{array}{l} \int (x + 2) (3 x + 1) d x \\ = \int 3 x^{2} + 7 x + 2 d x \\ = \int 3 x^{2} d x + \int 7 x d x + \int 2 d x \\ = \frac{3 x^{3}}{3} + \frac{7 x^{2}}{2} + 2 x + c \\ = x^{3} + \frac{7 x^{2}}{2} + 2 x + c \end{array}

Contoh 3:

\begin{array}{l} \int \frac{3 x^{3} + x^{2} - x}{x} d x \\ = \int (3 x^{2} + x - 1) d x \\ = \int 3 x^{2} d x + \int x d x - \int 1 d x \\ = \frac{3 x^{3}}{3} + \frac{x^{2}}{2} - x + c \\ = x^{3} + \frac{x^{2}}{2} - x + c \end{array}