Bab 10 Penyelesaian Segitiga

Posted on May 27, 2016 by user

Bab 10 Penyelesaian Segitiga

10.1 Petua Sinus

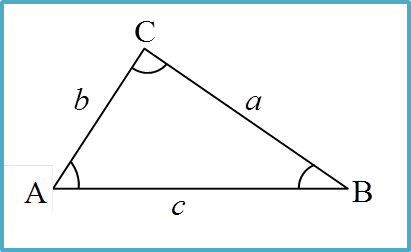
Dalam suatu segitiga ABC, huruf besar A, B, C digunakan untuk mewakili sudut di bucu-bucu A, B dan C masing-masing. Huruf kecil a, b, dan c untuk mewakili sisi BC, CA dan AB yang bertentangan dengan bucunya.

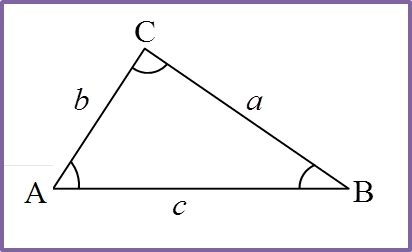
Petua sinus boleh digunakan untuk menyelesaikan sesuatu segitiga apabila
(i) dua sudut dan satu sisi diberikan, atau
(ii) dua sisi dan satu sudut bukan kandung diberikan

(A) Jika 2 sudut dan 1 sisi diketahui ⇒ Petua Sinus

Contoh:

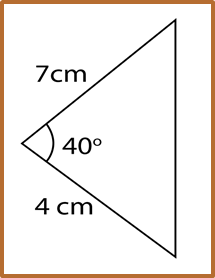
Hitung panjang AB, dalam cm.

Penyelesaian:

∠ACB = 180^o – (50^o + 70^o) = 60^o

\begin{array}{l} \frac{A B}{\sin 60^{o}} = \frac{4}{\sin 50^{o}} \\ A B = \frac{4 \times \sin 60^{o}}{\sin 50^{o}} \\ A B = 4.522 cm \end{array}

(B) Jika 2 sisi dan 1 sudut diketahui (bukan di antara sisi) ⇒ Petua Sinus

Contoh:

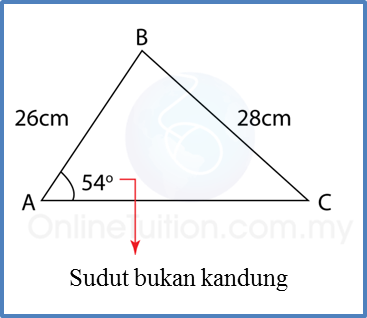
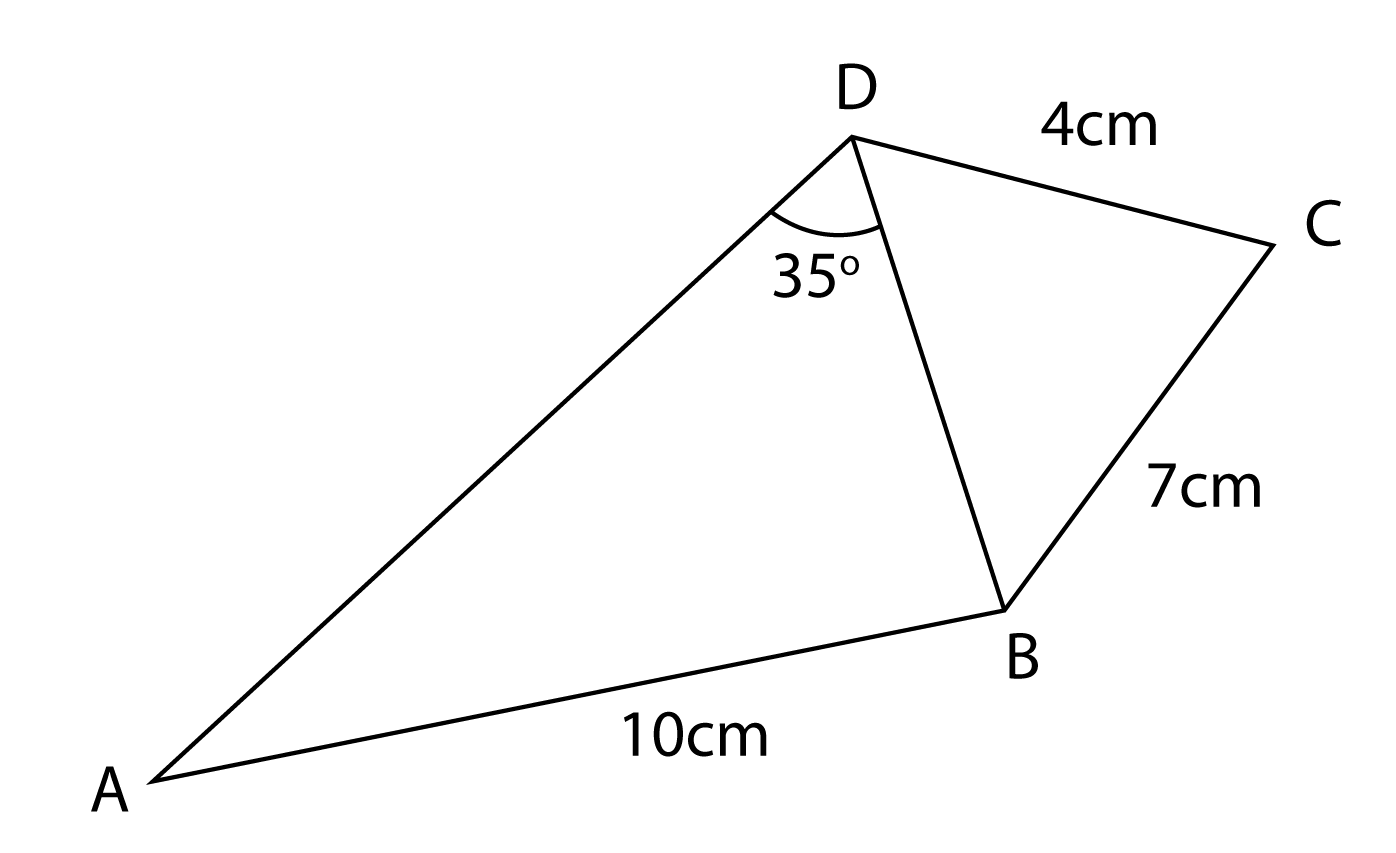
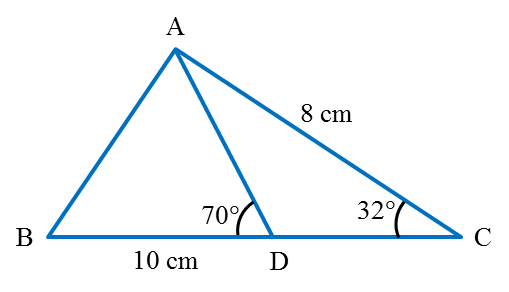
Hitung ∠ACB

Penyelesaian:

\begin{array}{l} \frac{28}{\sin 54^{o}} = \frac{26}{\sin ∠ A C B} \\ \sin ∠ A C B = \frac{26 \times \sin 54^{o}}{28} \\ \sin ∠ A C B = 0.7512 \\ ∠ A C B = {48.7}^{o} \end{array}

(C) Mencari Sisi atau Sudut dalam Sesuatu Segitiga bagi Kes Berambiguiti

Contoh:

Hitung ∠ACB, θ.

Penyelesaian:

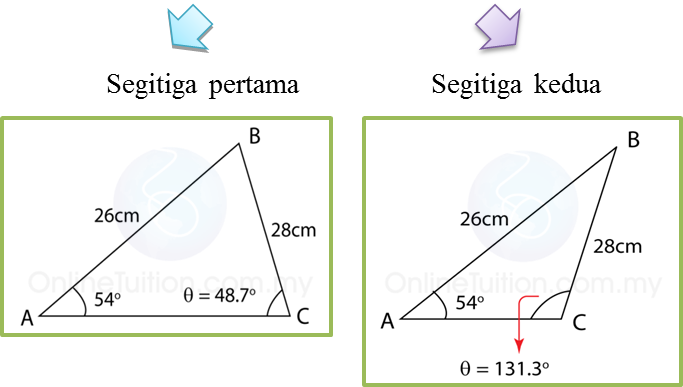
Dalam kes ini, terdapat dua kemungkinan dalam bentuk sigitiga.

AB = 26cm BC = 28 cm ∠ BAC = 54^o

\frac{26}{\sin θ} = \frac{28}{\sin 54^{o}}

sin θ = 0.7512

θ = sin ^-10.7512

θ = 48.7^o, 180^o – 48.7^o

θ = 48.7^o(sudut tirus), 131.3^o (sudut cakah)

Bab 10 Penyelesaian Segitiga

Posted on May 27, 2016 by user

10.2 Petua Kosinus

a² = b²+ c² – 2bc kosA

b² = a²+ c² – 2ac kosB

c² = a²+ b² – 2ab kosC

Petua kosinus boleh digunakan untuk menyelesaikan sesuatu segitiga apabila
(i) dua sisi dan satu sudut kandung diberikan, atau
(ii) tiga sisi diberikan

(A) Jika 2 sisi dan 1 sudut kandung diberi ⇒ Petua Kosinus

Contoh:

Hitung panjang AC, x, dalam cm bagi segitiga di atas.

Penyelesaian:

b² = a²+ c² – 2ac kosB

x² = 4² + 7² – 2(4)(7) kos50^o

x² = 16 + 49 – 56 (0.6428)

x² = 65 – 35.997

x² = 29.003

x = 5.385 cm

(B) Jika 3 sisi diberi ⇒ Petua Kosinus

Contoh:

Hitung ∠BAC

Penyelesaian:

\begin{array}{l} k o s A = \frac{b^{2} + c^{2} - a^{2}}{2 b c} \\ k o s ∠ B A C = \frac{7^{2} + 6^{2} - 8^{2}}{2 (7) (6)} \end{array}

kos∠BAC = 0.25

∠BAC = kos ^-10.25

∠BAC = 75.52^o

Bab 10 Penyelesaian Segitiga

Posted on May 26, 2016 by user

10.4.1 Penyelesaian Segitiga, SPM Praktis (Kertas 2)

Soalan 1:

Rajah di bawah menunjukkan sisi empat ABCD.

Luas segitiga BCD ialah 12 cm² dan ∠BCD ialah tirus. Hitung
(a) ∠BCD,
(b) Panjang, dalam cm, bagi BD,
(c) ∠ABD,
(d) luas, dalam cm², sisi empat ABCD.

Penyelesaian:

(a)

Diberi luas ∆ BCD = 12 cm²

½ (BC) (CD) sin C = 12

½ (7) (4) sin C= 12

14 sin C = 12

sin C = 12/14 = 0.8571

C = 59^o

∠BCD = 59^o

(b)

Guna petua kosinus,

BD² = CD² + BC² – 2 (4)(7) kos 59^o

BD² = 4² + 7² – 2 (4)(7) kos 59^o

BD² = 65 – 28.84

BD² = 36.16

BD = 6.013 cm

(c)

Guna petua sinus,

\begin{array}{l} \frac{A B}{\sin 35^{\circ}} = \frac{6.013}{\sin A} \\ \frac{10}{\sin 35^{\circ}} = \frac{6.013}{\sin A} \\ \sin A = \frac{6.013 \times \sin 35^{\circ}}{10} \end{array}

sin A = 0.3449

A = 20.18^o

∠ABD = 180^o– 35^o – 20.18^o

= 124.82^o

(d)

Luas sisi empat ABCD

= Luas ∆ ABD + Luas ∆ BCD

= ½ (AB)(BD) sin B + 12 cm

= ½ (10) (6.013) sin 124.82 + 12

= 24.68 + 12

= 36.68 cm

Bab 10 Penyelesaian Segitiga

Posted on May 26, 2016 by user

10.3 Luas Segitiga

Luas segitiga = ½ absinC

Contoh:

Hitung luas segitiga rajah di atas.

Penyelesaian:

Luas ∆ = ½ ab sinC

= ½ (7)(4) sin40^o

= 9 cm²

Contoh:

Rajah di atas menunjukkan sebuah segi tiga ABC, dengan keadaan AC = 8 cm dan ∠ C = 32^o . Titik D terletak pada garis BC dengan keadaan BD = 10 cm dan ∠ ADB = 70^o . Hitungkan
(a) panjang CD,
(b) luas ∆ ADC,
(c) luas ∆ ABC,
(d) panjang AB.

Penyelesaian:
(a)

\begin{array}{l} ∠ A D C + 70^{o} = 180^{o} \\ ∠ A D C = 110^{o} \\ ∠ C A D = 180^{o} - 110^{o} - 32^{o} \\ ∠ C A D = 38^{o} \\ Guna Petua Sinus, \\ \frac{8}{\sin 110^{o}} = \frac{C D}{\sin 38^{o}} \\ C D \sin 110^{o} = 8 \sin 38^{o} \\ C D (0.940) = 8 (0.616) \\ C D = 5.243 \end{array}

(b)

\begin{array}{l} Luas △ A D C \\ = \frac{1}{2} (8) (5.243) sin 32^{o} \\ = 20.972 (0.530) \\ = 11.12 {cm}^{2} \end{array}

(c)

\begin{array}{l} Luas △ A B C \\ = \frac{1}{2} (8) (10 + 5.243) sin 32^{o} \\ = 60.972 (0.530) \\ = 32.315 {cm}^{2} \end{array}

(d)

\begin{array}{l} Guna Petua kosinus bagi △ A B C, \\ A B^{2} = {15.243}^{2} + 8^{2} - 2 (15.243) (8) k o s 32^{o} \\ A B^{2} = 232.35 + 64 - 206.83 \\ A B^{2} = 89.52 \\ A B = 9.462 cm \end{array}

Bab 6 Geometri Koordinat

Posted on May 26, 2016 by user

6.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 2:

Rajah menunjukkan trapezium PQRS. Diberi persamaan PQialah 2y – x – 5 = 0, cari

(a) nilai w,

(b) persamaan PS dan seterusnya cari koordinat P,

(c) lokus M supaya segitiga QMS adalah sentiasa berserenjang di M.

Penyelesaian:

(a)

Persamaan PQ,

2y – x – 5 = 0

2y = x + 5

\begin{array}{l} y = \frac{1}{2} x + \frac{5}{2} \\ ∴ m_{P Q} = \frac{1}{2} \\ In a trapizium, m_{P Q} = m_{S R} \\ \frac{1}{2} = \frac{0 - (- 3)}{w - 4} \\ w - 4 = 6 \\ w = 10 \end{array}

(b)

\begin{array}{l} m_{P Q} = \frac{1}{2} \\ m_{P S} = - \frac{1}{m_{P Q}} = - \frac{1}{\frac{1}{2}} = - 2 \end{array}

Titik S = (4, –3), m = –2

y – y₁ = m (x– x₁)

y – (–3) = –2 (x – 4)

y + 3 = –2x + 8

y = –2x + 5

Persamaan PS ialah y = –2x + 5

PS is y = –2x + 5-----(1)

PQ is 2y = x + 5-----(2)

Gantikan (1) ke dalam (2)

2 (–2x + 5) = x + 5

–4x + 10 = x + 5

–5x = –5

x = 1

Dari (1), y = –2(1) + 5

y = 3

Koordinat titik P = (1, 3).

(c)

Katakan M = (x, y)

Diberi ∆QMS berserenjang di M

Oleh itu, ∆QMS = 90^o

(m_QM) (m_MS) = –1

(\frac{y - 5}{x - 5}) (\frac{y - (- 3)}{x - 4}) = - 1

(y – 5) (y + 3) = –1(x– 5) (x – 4)

y² + 3y – 5y – 15 = –1(x² – 4x – 5x + 20)

y² – 2y – 15 = –x² + 9x – 20

x² + y²– 9x – 2y + 5 = 0

Jadi, persamaan lokus titik M ialah

x² + y² – 9x – 2y + 5 = 0.

Bab 6 Geometri Koordinat

Posted on May 26, 2016 by user

6.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 1:

Rajah menunjukkan garis lurus PQ bertemu dengan garis lurus RSdi titik Q. Titik P terletak pada paksi-y.

(a) Tuliskan persamaan RS dalam bentuk pintasan.

(b) Diberi 2RQ = QS, cari koordinat Q.

(c) Diberi PQ berserenjang dengan RS, cari pintasan-y bagi PQ.

Penyelesaian:

(a)

\begin{array}{l} \frac{x}{12} + \frac{y}{- 6} = 1 \\ \frac{x}{12} - \frac{y}{6} = 1 \end{array}

(b)

Diberi 2RQ = QS

\begin{array}{l} \frac{R Q}{Q S} = \frac{1}{2} \\ Katakan koordinat Q = (x, y) \\ (\frac{(0) (2) + (12) (1)}{1 + 2}, \frac{(- 6) (2) + (0) (1)}{1 + 2}) = (x, y) \\ x = \frac{12}{3} = 4 \\ y = - \frac{12}{3} = - 4 \\ Q = (4, - 4) \end{array}

(c)

\begin{array}{l} Kecerunan R S, m_{R S} \\ = - (\frac{- 6}{12}) = \frac{1}{2} \\ m_{P Q} = - \frac{1}{m_{R S}} = - \frac{1}{\frac{1}{2}} = - 2 \end{array}

Titik Q = (4, –4), m = –2

Guna y = mx+ c

–4 = –2 (4) + c

c = 4

Maka, pintasan-y bagi PQ = 4

Bab 6 Geometri Koordinat

Posted on May 26, 2016 by user

6.7 Geometri Koordinat, SPM Praktis (Soalan Pendek)

Soalan 3

Persamaan garis lurus CD dan EF adalah 5x + y – 4 = 0 dan

\frac{x}{7} - \frac{y}{h} = 1

. Jika CD dan EF adalah selari, cari nilai h.

Penyelesaian:

Dua garis selari mempunyai kecerunan yang sama.

5x + y – 4 = 0

y = –5x + 4, m_CD= –5

Bagi garis lurus EF,

\begin{array}{l} \frac{x}{7} - \frac{y}{h} = 1 \\ m_{E F} = - (\frac{pintasan- y}{pintasan- x}) = - (\frac{- h}{7}) = \frac{h}{7} \\ m_{C D} = m_{E F} \\ - 5 = \frac{h}{7} \\ h = - 35 \end{array}

Soalan 4

Garis lurus

\frac{x}{5} + \frac{y}{p} = 1

mempunyai pintasan-y bernilai 3 dan selari dengan garis lurus y + qx = 0. Tentukan nilai p dan nilai q.

Penyelesaian:

Diberi pintasan-ygaris lurus

\frac{x}{5} + \frac{y}{p} = 1

adalah 3,

Maka p = 3

Kecerunan garis lurus

= - \frac{3}{5}

Bagi garis y + qx = 0, y = –qx

Dua garis selari mempunyai kecerunan yang sama,

\begin{array}{l} - q = - \frac{3}{5} \\ q = \frac{3}{5} \end{array}

Soalan 5

Persamaan dua garis lurus

\frac{y}{7} + \frac{x}{4} = 1

dan 7y = 4x+ 21. Tentukan sama ada pasangan garis lurus adalah berserenjang antara satu sama lain.

Penyelesaian:

\begin{array}{l} Bagi garis lurus \frac{y}{7} + \frac{x}{4} = 1, \\ kecerunan = - \frac{7}{4} \\ Bagi garis lurus 7 y = 4 x + 21, \\ y = \frac{4}{7} x + 3, \\ kecerunan = \frac{4}{7} \\ - \frac{7}{4} \times \frac{4}{7} = - 1 \end{array}

Maka, pasangan garis lurus adalah berserenjang antara satu sama lain.

Bab 6 Geometri Koordinat

Posted on May 26, 2016 by user

6.6 Persamaan Lokus yang Melibatkan Jarak di antara Dua Titik

1. Persamaan lokus bagi suatu titik bergerak P (x, y) supaya jaraknya (r) dari suatu titik tetap (x₁, y₁) adalah malar.

(x– x₁)² + (y – y₁)²= r²

2. Persamaan lokus bagi suatu titik bergerak P (x, y) supaya jaraknya sentiasa malar dari dua titik tetap (x₁, y₁) dan (x₁, y₁) dengan nisbah m : n ialah

3. Persamaan lokus bagi suatu titik bergerak P (x, y) supaya jaraknya sentiasa malar dari dua titik tetap A dan B adalah pembahagi dua sama serenjang garis AB.

Contoh 1:

Cari persamaan lokus bagi titik bergerak P (x, y) supaya jaraknya sentiasa 5 unit dari suatu titik tetap Q (2, 4).

Penyelesaian:

(x – x₁)²+ (y – y₁)² = r²

(x – 2)² + (y – 4)² = 5²

x² – 4x + 4 + y² – 8y + 16 = 25

x² + y²– 4x – 8y – 5 = 0

Contoh 2:

Cari persamaan lokus bagi titik bergerak P (x, y) supaya jaraknya dari titik A(–2, 3) dan titik B (4, –1) adalah sama.

Penyelesaian:

PA = PB

\sqrt{{(x - (- 2))}^{2} + {(y - 3)}^{2}} = \sqrt{{(x - 4)}^{2} + {(y - (- 1))}^{2}}

Kuasa duakan kedua-dua belah persamaan

(x + 2)² + (y – 3)² = (x – 4)²+ (y + 1)²

x² + 2x + 4 + y² – 6y + 9 = x² – 8x + 16 + y² + 2y + 1

10x – 8y – 4 = 0

Jadi, persamaan lokus titik P ialah, 10x – 8y – 4 = 0

Contoh 3:

A (2, 0) dan B (0, -2) adalah dua titik tetap. Titik P bergerak dengan nisbah supaya AP : PB = 1 : 2. Cari persamaan lokus bagi titik bergerak P.

Penyelesaian:

AP: PB = 1: 2

\begin{array}{l} \frac{A P}{P B} = \frac{1}{2} \\ 2 A P = P B \\ 2 \sqrt{{(x - 2)}^{2} + {(y - 0)}^{2}} = \sqrt{{(x - 0)}^{2} + {(y - (- 2))}^{2}} \end{array}

Kuasa duakan kedua-dua belah persamaan

4[(x – 2)² + y²] = x² + (y + 2)²

4 (x² – 4x + 4 + y²) = x² + y²+ 4y + 4

4x² – 16x + 16 + 4y² = x² + y² + 4y + 4

3x² + 3y²– 16x – 4y + 12 = 0

Jadi, persamaan lokus titik P ialah, 3x² + 3y² – 16x – 4y +12 = 0

Bab 6 Geometri Koordinat

Posted on May 25, 2016 by user

6.5 Garis Lurus Selari dan Garis Lurus Serenjang

(A) Garis Lurus Selari
1. Jika dua garis lurus adalah selari, maka kecerunannya adalah sama.

Dalam rajah di atas, jika garis lurus L₁adalah selari dengan garis lurus L₂, maka
kecerunan L₁= kecerunan L₂.
m₁ = m₂

Contoh 1:

Diberi persamaan suatu garis lurus adalah selari dengan x + 8y = 40 dan melalui titik A (2, 3k) dan titik B (–6, 4k²), cari nilai k.

Penyelesaian:

x + 8y = 40

8y = –x + 40

y = –⅛ x + 5

Kecerunan m₁= –⅛

Diberi garis lurus melalui titik A and titik B adalah selari dengan x + 8y = 40, maka m₁= m₂

- \frac{1}{8} = \frac{4 k^{2} - 3 k}{- 6 - 2}

8 = 32k²– 24k

1 = 4k²– 3k

4k²– 3k – 1 = 0

(4k + 1)(k – 1) = 0

4k + 1 = 0 atau k – 1 = 0

k = –¼ k = 1

(B) Garis Lurus Serenjang

1. Jika dua garis lurus berserenjang antara satu sama lain, maka hasil darab kecerunan-kecerunannya adalah –1.

Dalam rajah di atas, jika garis lurus L₁adalah berserenjang dengan garis lurus L₂, maka
kecerunan L₁× kecerunan L₂ = –1.
m₁ × m₂ = –1

Contoh 2:

Diberi titik-titik P(–2, 4), Q (4, 2), R (–1, –3) dan S (2, 6), tunjukkan PQ berserenjang dengan RS.

Penyelesaian:

\begin{array}{l} m_{P Q} = \frac{2 - 4}{4 - (- 2)} = - \frac{1}{3} \\ m_{R S} = \frac{6 - (- 3)}{2 - (- 1)} = 3 \\ (m_{P Q}) (m_{R S}) = (- \frac{1}{3}) (3) = - 1 \end{array}

Maka, PQ berserenjang dengan RS.

Bab 6 Geometri Koordinat

Posted on May 25, 2016 by user

6.4.2 Persamaan Garis Lurus (Bahagian 2)

(C) Pembentukan Persamaan Garis Lurus

Kes 1

1. Kecerunan dan koordinat-koordinat satu titik diberi.

2. Persamaan garis lurus dengan kecerunan, m melalui titik (x₁, y₁) ialah

y – y₁= m (x – x₁)

Soalan 1:

Suatu garis lurus dengan kecerunan –3 melalui titik (–1, 5). Cari persamaan garis itu.

Penyelesaian:

y – y₁= m (x – x₁)

y – 5= – 3 (x – (–1))

y – 5= – 3x – 3

y= – 3x + 2

Kes 2

1. Koordinat-koordinat dua titik diberi.

2. Persamaan garis lurus yang melalui titik (x₁, y₁) dan titik (x₂, y₂) ialah

\frac{y - y_{1}}{x - x_{1}} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}

Soalan 2:

Cari persamaan garis lurus yang melalui titik (2, 4) dan titik (5, 6).

Penyelesaian:

\begin{array}{l} \frac{y - y_{1}}{x - x_{1}} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ Katakan (x_{1}, y_{1}) = (2, 4) \\ dan (x_{2}, y_{2}) = (5, 6) \\ \frac{y - 4}{x - 2} = \frac{6 - 4}{5 - 2} \\ \frac{y - 4}{x - 2} = \frac{2}{3} \\ 3 y - 12 = 2 x - 4 \\ 3 y = 2 x + 8 \end{array}

Kes 3

1. Pintasan-x dan pintasan-y diberi:

\frac{x}{a} + \frac{y}{b} = 1

a = pintasan-x

b = pintasan-y

Soalan 3:

Cari persamaan garis lurus yang melalui titik (5, 0) dan titik (0, –6).

Penyelesaian:

Pintasan-x, a = 5, Pintasan-y, b = –6

Persamaan garis lurus

\begin{array}{l} \frac{x}{a} + \frac{y}{b} = 1 \\ \frac{x}{5} + \frac{y}{(- 6)} = 1 \\ \frac{x}{5} - \frac{y}{6} = 1 \end{array}

(D) Bentuk-bentuk Persamaan Garis Lurus

(a) Bentuk Kecerunan
Persamaan dalam bentuk kecerunan
y = mx + c
m = kecerunan
c = pintasan-y

(b) Bentuk Am
Persamaan dalam bentuk am
ax² + bx + c = 0

(c) Bentuk Pintasan

\frac{x}{a} + \frac{y}{b} = 1

a = pintasan-x
b = pintasan-y