Bab 5 Garis Lurus

Posted on by

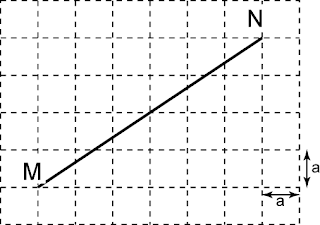
5.6.1 SPM Praktis (Soalan Pendek)
 
Soalan 1:
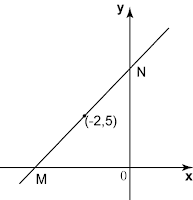
Rajah di bawah menunjukkan suatu garis lurus RS yang dilukis pada satah Cartesan.


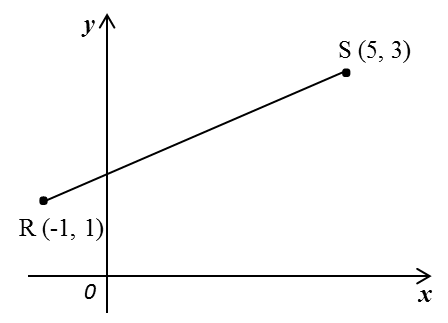
Cari kecerunan RS.

Penyelesaian:
Guna formula kecerunan y 2 − y 1 x 2 − x 1 Kecerunan R S = 3 − 1 5 − ( − 1 ) = 2 6 = 1 3



Soalan 2:
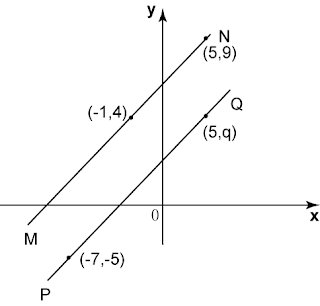
Dalam rajah di bawah, PQ adalah suatu garis lurus dengan kecerunan –½.


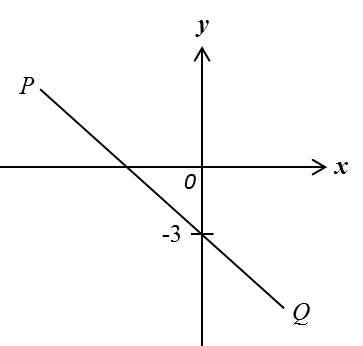
Cari pintasan-x bagi garis lurus PQ.

Penyelesaian:
m = − pintasan- y pintasan- x − 1 2 = − ( − 3 pintasan- x ) pintasan- x = 3 × ( − 2 ) = − 6



Soalan 3:
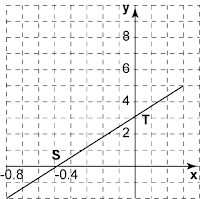
Rajah di bawah menunjukkan suatu garis lurus RS yang dilukis pada satah Cartesan.


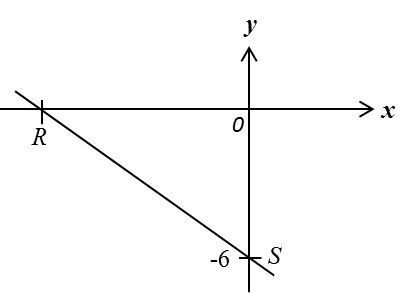
Diberi jarak antara RS ialah 10 unit.
Cari kecerunan RS.

Penyelesaian:
RS=10 unit, OS=6 unit OR= 10 2 − ( −6 ) 2 =8 unit pintasan-y bagi RS=−6 pintasan-x of RS=−8

m=− pintasan-y pintasan-x ∴ Kecerunan RS=−( −6 −8 )=− 3 4



Soalan 4:
Kecerunan bagi garis lurus 3x – 4y = 24 ialah

Penyelesaian:
Menyusun semula persamaan dalam bentuk y = mx+ c
3x – 4y = 24
4y = 3x – 24
y = 3 4 x − 6  

Oleh itu, kecerunan garis lurus = 3 4 .  


Soalan 5:
Tentukan pintasan-y bagi garis lurus 3x + 2y = 5

Penyelesaian:
Bagi pintasan-y, x = 0
3(0) + 2y = 5
y = 5 2 Oleh itu, pintasan- y = 5 2 .


Bab 5 Garis Lurus

Posted on by
5.5 Garis Selari (Contoh Soalan)

Soalan 1:

Dalam rajah di atas, garis lurus MN dan PQ adalah selari. Cari nilai q.
Penyelesaian:
Garis lurus yang selari mempunyai kecerunan yang sama.
m1 = m2
mMN = mPQ

Guna formula kecerunan  y 2 − y 1 x 2 − x 1 9−4 5−( −1 ) = q−( −5 ) 5−( −7 ) 5 6 = q+5 12
60 = 6q + 30
6q = 30
q= 5

Bab 5 Garis Lurus

Posted on by
5.4 Persamaan Garis Lurus (Contoh Soalan)

Soalan 1:
Diberi persamaan bagi suatu garis lurus ialah 4x + 6y – 3 = 0. Apakah kecerunan garis lurus ini?
Penyelesaian:
4x+6y−3=0 6y=−4x+3 y=− 4x 6 + 3 6 y=− 2 3 x+ 1 2 y=mx+c kecerunan, m=− 2 3

Soalan 2:
Diberi persamaan bagi suatu garis lurus ialah y = – 7x + 3. Cari pintasan-ybagi garis ini.
Penyelesaian:
y= mx + c, c ialah pintasan- y garis lurus.
Oleh itu, bagi garis lurus y = – 7x + 3,
Pintasan-yialah 3


Soalan 3:

Cari persamaan bagi garis lurus MN jika kecerunannya ialah 3.
Penyelesaian:
Diberi m = 3
Gantikan nilai m= 3 dan (–2, 5) ke dalam y = mx + c.
5 = 3 (–2) + c
5 = –6 + c
c= 11

Oleh itu, persamaan bagi garis lurus MN ialah y = 3x + 11.

Bab 5 Garis Lurus

Posted on by
5.4 Persamaan Garis Lurus
1.      Jika nilai kecerunan, m, dan pintasan-y, cdiberi, maka satu persamaan garis lurus y= mx + c boleh dibentuk.
2.      Jika suatu garis lurus diwakili oleh persamaan berbentuk y = mx + c, maka
          (a)  m ialah kecerunan,
          (b)  c ialah pintasan-y

Contoh 1:
Diberi persamaan bagi suatu garis lurus ialah y = 3 – 4x. Cari kecerunan dan pintasan-ybagi garis ini.
Penyelesaian:
y= 3 – 4x
y= – 4x + 3 ← (y = mx + c)
Oleh itu, kecerunan, m = – 4
pintasan-y, c = 3

3.      Jika suatu persamaan garis lurus ditulis dalam bentuk ax + by + c = 0, maka tukarnya kepada bentuk y = mx+ c untuk mencari nilai kecerunan dan pintasan-y.

Contoh 2:
Diberi persamaan bagi suatu garis lurus ialah 4x + 6y– 3 = 0. Cari kecerunan dan pintasan-ybagi garis ini.
Penyelesaian:
4x + 6y – 3 = 0
6y = –4 x + 3
y=− 2 3 x+ 1 2 ← y=mx+c ∴ Kecerunan m=− 2 3      pintasan-y, c= 1 2

Bab 5 Garis Lurus

Posted on by
5.3 Pintasan (Contoh Soalan)

Soalan 1:

Pintasan-x bagi garis lurus ST ialah
Penyelesaian:
Koordinat-x bagi titik persilangan pada garis lurus dengan paksi-x ialah –0.4.
Oleh itu, pintasan-x bagi garis lurus ST ialah –0.4.

Soalan 2:
Cari pintasan-x bagi garis lurus 2x + 3y+ 6 = 0.
Penyelesaian:
2x + 3y + 6 = 0
Pada pintasan-x, y = 0
2x + 3(0) + 6 = 0
2x = –6
x= –3

Soalan 3:
Cari pintasan-y bagi garis lurus 12x – 15y = 60.
Penyelesaian:
12x – 15y = 60
Pada pintasan-y, x = 0
12(0) – 15y= 60
–15y = 60
y = –4

Bab 5 Garis Lurus

Posted on by
5.2 Kecerunan Garis Lurus dalam Sistem Koordinat Cartesan (Contoh Soalan)

Soalan 1:
Suatu garis lurus adalah melalui titik (–3, –7) dan (4, 14). Apakah kecerunan garis lurus tersebut?
Penyelesaian:
Katakan (x1, y1) = (-3, –7) dan (x2, y2) = (4, 14).
kecerunan garis lurus
= y 2 − y 1 x 2 − x 1 = 14−( −7 ) 4−( −3 ) = 21 7 =3


Soalan 2:


Kecerunan garis lurus PQ dalam rajah di atas ialah
Penyelesaian:
Katakan (x1, y1) = (12, 0) dan (x2, y2) = (0, 7).
Kecerunan garis lurus PQ
= y 2 − y 1 x 2 − x 1 = 7−0 0−12 =− 7 12

Soalan 3:
Suatu garis lurus dengan kecerunan –3 melalui titik (–4, 6) dan (–1, p). Cari nilai p.
Penyelesaian:
y 2 − y 1 x 2 − x 1 =−3 p−6 −1−( −4 ) =−3 p−6 3 =−3 p−6=−9 p=−3


Bab 5 Garis Lurus

Posted on by
5.2 Kecerunan Garis Lurus dalam Sistem Koordinat Cartesan

Mengira Kecerunan Garis Lurus
Kecerunan, m, satu garis lurus yang melalui titik P (x1 , y1) dan Q (x2 , y2) ialah,
m PQ = y 2 − y 1 x 2 − x 1

Contoh 1:

Hitung kecerunan garis lurus yang melalui titik P dan Q dalam rajah di atas.
Penyelesaian:
P= (x1, y1) = (4, 3), Q = (x2, y2) = (10, 5)
Kecerunan garis lurus PQ
= y 2 − y 1 x 2 − x 1 = 5−3 10−4 = 2 6 = 1 3


Contoh 2:
Hitung kecerunan garis lurus yang melalui titik A (7, –3) dan titik B (–3, 6).
Penyelesaian:
A= (x1, y1) = (7, –3), B = (x2, y2) = (–3, 6)

Kecerunan garis lurus AB
= y 2 − y 1 x 2 − x 1 = 6−( −3 ) −3−7 =− 9 10


Bab 5 Garis Lurus

Posted on by
5.1 Kecerunan Garis Lurus

Kecerunan garis lurus ialah nisbah jarak mencancang kepada jarak mengufuk di antara dua titik pada garis itu. 

Kecerunan garis lurus, m= Jarak mencancang Jarak mengufuk

Contoh:

Cari kecerunan bagi garis lurus di atas.

Penyelesaian:
Kecerunan, m= Jarak mencancang Jarak mengufuk                     = 4 unit 6 unit                     = 2 3


Bab 2 Ungkapan dan Persamaan Kuadratik

Posted on by
SPM Praktis (Soalan Panjang)
Soalan 5:
Selesaikan persamaan kuadratik
(m + 2)(m – 4) = 7(m – 4).

Penyelesaian:
(m + 2)(m – 4) = 7(m – 4)
m2 – 4m + 2m – 8 = 7m – 28
m2 – 9m + 20 = 0
(m – 5)(m – 4) = 0
m= 5    or    m= 4   


Soalan 6:
Selesaikan persamaan kuadratik
−6y−2 y = 7 1−y


Penyelesaian:
− 6 y − 2 y = 7 1 − y ( − 6 y − 2 ) ( 1 − y ) = 7 y − 6 y + 6 y 2 − 2 + 2 y − 7 y = 0 6 y 2 − 11 y − 2 = 0 ( 6 y + 1 ) ( y − 2 ) = 0 6 y + 1 = 0         or         y = 2 y = − 1 6


Soalan 7:
Selesaikan persamaan kuadratik
4m 7 =m( 8m−9 )

Penyelesaian:
4m 7 =m( 8m−9 ) 4m=7m( 8m−9 ) 4m=56 m 2 −63m 56 m 2 −63m−4m=0 56 m 2 −67m=0 m(56m−67)=0 m=0        or        56m−67=0                                        m= 67 56


Soalan 8:

Rajah di atas menunjukkan sebuah segi empat tepat ABCD.
     (a)  Ungkapkan luas ABCD dalam sebutan x,
     (b)  Diberi luas ABCD ialah 60 cm2, cari panjang AB.

Penyelesaian:
(a)
Luas ABCD
= (n + 7) × n
= (n2+ 7n) cm2
(b)
Diberi luas ABCD= 60
n2 + 7n = 60
n2 + 7n – 60 = 0
(n – 5) (n + 12) = 0
n= 5    or    n = – 12 (tidak diterima)

Apabila n= 5,
Panjang AB = 5 + 7 = 12 cm

Bab 2 Ungkapan dan Persamaan Kuadratik

Posted on by
SPM Praktis (Soalan Panjang)

Soalan 1:
Selesaikan persamaan kuadratik, (y + 3)(y – 4) = 30

Penyelesaian:
(y + 3)(y – 4) = 30
y2 – 4y + 3y – 12 = 30
y2 – y – 12 – 30 = 0
y2 – y – 42 = 0
(y + 6)(y – 7) = 0
y+ 6 = 0, y = –6
y– 7 = 0
y = 7


Soalan 2:
Selesaikan persamaan kuadratik, 5x2 = 3( x – 2) + 8

Penyelesaian:
5x2= 3( x – 2) + 8
5x2= 3x – 6 + 8
5x2– 3x – 2 = 0
(5x + 2)(x – 1) = 0
5x + 2 = 0, x = − 2 5
Or
x– 1 = 0
x= 1


Soalan 3:
Selesaikan persamaan kuadratik, 2 p 2 −15 p =7

Penyelesaian:
2 p 2 −15 p =7 

2p2– 15 = 7p
2p2–7p – 15 = 0
(2p + 3)(p – 5) = 0
2p + 3 = 0, p =  
p– 5 = 0
p= 5


Soalan 4:
Selesaikan persamaan kuadratik, y( y− 9 2 )= 5 2

Penyelesaian:
y( y− 9 2 )= 5 2 y 2 − 9y 2 = 5 2

(×2), 2y2– 9y = 5
2y2– 9y – 5 = 0
(2y + 1)(y – 5) = 0
2y + 1 = 0, y = ½
Or
y– 5 = 0
y = 5