3.5.1 SPM Practis (Soalan Panjang)
Soalan 1:
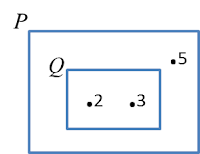
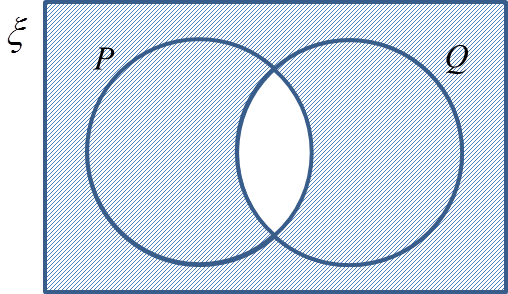
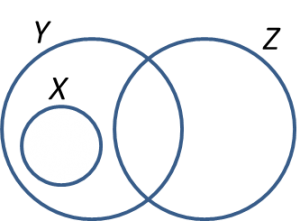
Gambar rajah Venn di ruang jawapan menunjukkan set X, set Y dan set Z dengan keadaan set semesta,
Pada rajah di ruang jawapan, lorekkan
Penyelesaian:
(a) X’ ∩ Y menunjukkan persilangan rantau di luar set X dengan rantau set Y.
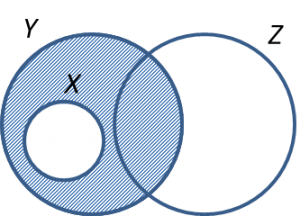
(b)
· Cari rantau
·
bermaksud kesatuan rantau X dengan rantau di luar Y.
· Persilangan rantau ini dengan rantau Z untuk membentuk

Soalan 2:
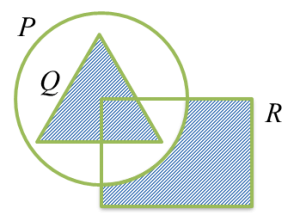
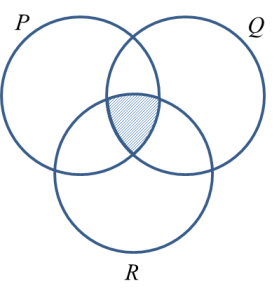
Gambar rajah Venn di ruang jawapan menunjukkan set P, set Q dan set R dengan keadaan set semesta,
Pada rajah di ruang jawapan, lorekkan(a) Q ∩ R,
(b)
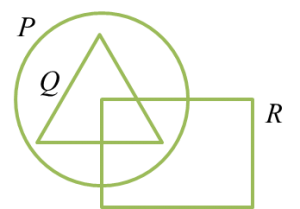
Penyelesaian:
(a) Q ∩ R menunjukkan persilangan rantau Q dengan rantau R.
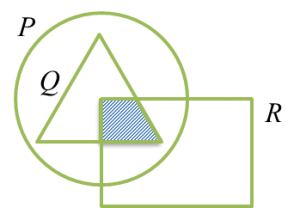

(b)
· Cari rantau (P’ ∩ R).
· (P’ ∩ R) bermaksud persilangan rantau di luar P dengan rantau R.
· Kesatuan rantau ini dengan rantau Q untuk membentuk